I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
analisi Xrf quantitativa. eccitazione monocromatica
Si intende per analisi xrf quantitativa la determinazione delle concentrazioni relative in peso degli elementi chimici rivelati mediante l’analisi qualitativa. Le concentrazioni relative sono determinate nell’ipotesi che l’insieme degli elementi rilevati esaurisca la composizione del campione.
Le concentrazione si riferisce al contenuto relativo in peso dell’ elemento Pertanto, con l’analisi xrf non si ottengono informazioni sul tipo di composto chimico, se non indirettamente nel caso che le concentrazioni relative siano collegabili alla stechiometrica del composto e essa sia nota.
Inoltre, elementi leggeri, in particolare idrogeno, ossigeno e carbonio, sono tenuti in conto nell’analisi quantitativa solo nell’insieme come matrice assorbente. Ciò ha particolare interesse nei casi di analisi di vetri o ceramiche, come sarà discusso in seguito.
Le condizioni ideali, nelle quali l’analisi xrf quantitativa è relativamente facilitata, sono indicate di seguito (cfr. anche figura 1):
La condizione che lo spessore sia infinito è di solito verificata per i metalli, per i quali, infatti, uno spessore dell’ordine di 100 micron può considerarsi infinito, ma non è condizione necessaria per l’analisi quantitativa.
Si noti che con l’assumere l’omogeneità per la composizione a livello microscopico, si intende che essa esista su scala molto piccola in confronto con il percorso lineare medio compiuto dalla radiazione X incidente . Ricordiamo che l’omogeneità microscopica è condizione necessaria e sufficiente perché per l’auto assorbimento della radiazione di eccitazione e quello delle diverse righe X di emissione caratteristica sia calcolabile, per ogni energia, il coefficiente di assorbimento massivo totale come la combinazione lineare dei coefficienti di assorbimento massivi degli elementi contenuti nel campione pesati dalla concentrazione relativa per ogni elemento.
Tranne che nel caso di piccoli valori della concentrazione o, per lo meno, di piccole variazioni rispetto al valore medio, l’intensità della fluorescenza caratteristica non è proporzionale alla concentrazione dell’elemento nel campione. Ciò è dovuto all’effetto di auto assorbimento che dipende, come appena ricordato, dalla composizione del campione. Inoltre è da tenere presente l’effetto della eccitazione secondaria, della quale parleremo in seguito, cioè dell’eccitazione della fluorescenza X di elementi di peso medio o leggero dovuta alla presenza rilevante di elementi pesanti nello stesso campione.
L’effetto dell’auto assorbimento sull’intensità di emissione è illustrato nella figura 2. In essa è riportato l’andamento in funzione della concentrazione del rapporto Ii / I(i) tra l’intensità xrf Ii dell’elemento, i , distribuito omogeneamente nel campione con concentrazione relativa in peso , ci , e l’intensità I(i) da un campione dello stesso elemento puro (cioè, con ci = 1 ) La curva inferiore, con derivata seconda ovunque positiva, si riferisce al caso che l’auto-assorbimento del materiale del campione sia maggiore di quello del campione di elemento i puro. La curva superiore, con derivata seconda ovunque negativa, rappresenta il caso che l’auto-assorbimento sia minore nel campione in esame che nel campione di elemento puro.
Nel caso ideale che il campione composito presenti lo stesso assorbimento dell’elemento puro si avrebbe l’andamento lineare esteso a tutti i valori di concentrazione indicato con a) nella stessa figura.
L’operazione, preliminare all’analisi quantitativa, di ricavare dall’area del picco nello spettro X l’intensità di emissione al netto dal contributo del fondo e da quello dovuto a eventuali picchi parzialmente sovrapposti, si ottiene in modo diretto, e presenta trascurabili margini di errore, nel caso che la riga di fluorescenza sia dominante sul segnale del fondo e il picco sia ben isolato. Al contrario, in diversa condizione l’operazione di defolding dullo spettro X sperimentale, per ricavare i contributi netti delle diverse righe, può essere ottenuto solo attraverso procedure di best fitting sofisticate delle quali qui non ci occupiamo.
L’analisi quantitativa, che fornisce la concentrazione relativa in peso, é basata sulla misura dell’intensità di fluorescenza X per ogni elemento chimico rivelato, il termine analisi elementare per essa assume significato dal termine elemento in Chimica. Come già notato, l’analisi non dà, se non indirettamente, alcuna indicazione sulla natura del composto, ma solo la concentrazione relativa in peso per ciascun elemento rivelato
Dobbiamo, pertanto, trovre la relazione matematica fra l’intensità della riga X prodotta impiegando radiazione X di eccitazione, che nel caso più semplice supponiamo monocromatica, cioè di un solo valore di energia, E0 , e la concentrazione relativa dell’elemento chimico nel campione. Questa relazione dovrà contenere anche la dipendenza dell’intensità xrf dell’elemento dalle concentrazioni relative di tutti gli altri elementi rivelati nel campione. Trascurando, per il momento, la possibilità che si verifichino effetti di eccitazione secondaria, già citata, la fondamentale correzione dovuta alla composizione consiste nell’effetto di auto assorbimento all’interno del campione sia per la radiazione di eccitazione entrante che per quella delle riga X caratteristica emessa.
In linea di principio, dobbiamo eseguire un integrale su tutto il volume irradiato del campione in esame tenendo conto che, a causa dell’auto assorbimento, per ogni elemento di volume situato alla profondità x dalla superficie irraggiata, sia l’intensità della radiazione di eccitazione, prodotta da una sorgente di radiazione X monocromatica , sia l’intensità della radiazione emessa, rivelata dal rivelatore esterno, sono attenuate con legge di dipendenza esponenziale dallo spessore x attraversato nel campione.
Il calcolo risulta relativamente semplice se supponiamo che il campione abbia la forma di un pellet, cioè di un cilindretto del quale è irraggiata la superficie piana. La porzione della superficie sottoposta all’irraggiamento si suppone sufficientemente piccola e interna rispetto il bordo circolare del pellet.In queste condizioni, gli angoli ψ1 e ψ2 con la superficie possono essere considerati costanti. La fluorescenza X prodotta alla profondità x nel campione è emessa verso il rivelatore dotato di un’opportuna collimazione attraverso la stessa superficie piana irraggiata, Come è mostrato in figura 3, il generico elemento di volume di spessore infinitesimo dx alla profondità x riceve la radiazione di eccitazione attenuata lungo il percorso x / sinψ1 , mentre la radiazione di fluorescenza caratteristica emessa all’interno dell’ angolo solido sotteso dal rivelatore nella direzione ψ2, è attenuata nel percorso x / sinψ2 . L’approssimazione che l’estensione della superficie irraggiata, sia piccola, va intesa in confronto alla distanza del tubo X e a quella del rivelatore dalla superficie stessa. Anche il valore dello spessore x attraversato, dai raggi X nel campione è di solito di valore trascurabile rispetto le distanze della sorgente di eccitazione e del rivelatore dalla superficie irradiata.
In queste condizioni, il fattore di efficienza geometrica,G, che è dato principalmente dall’angolo solido del rilevatore, può essere considerato costante.
La condizione che gli angoli siano costanti è l’approssimazione fondamentale. Ad esempio, nel caso che la radiazione di eccitazione sia quella prodotta da un radio isotopo, è necessario che la disposizione geometrica del sistema sperimentale approssimi ragionevolmente bene questa ipotesi. Ciò è illustrato nella figura 4, che riporta due esempi rappresentanti schematicamente di una situazione sperimentale di analisi xrf nella quale si impiega un radioisotopo per l’eccitazione. Nel primo caso, gli angoli di irraggiamento e di emissione possono essere considerati costanti, mentre ciò non sarebbe corretto, per mancanza di una sufficiente collimazione, nel secondo caso.
Nello sviluppo delle relazioni per l’analisi quantitativa si farà uso della seguente simbologia (v. anche figura 5):
Nell’approssimazione che l’efficienza geometrica e gli angoli siano costanti, l’integrale sull’intero volume sotteso alla superficie irraggiata si riduce ad un integrale nella unica variabile x che rappresenta la profondità di penetrazione,Cioè, si ha
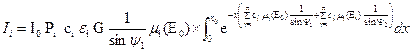
L’assorbimento totale dovuto allo spessore x ,infatti, è il prodotto dell’assorbimento della radiazione di eccitazione per quello della radiazione caratteristica emessa. Essendo il prodotto di 2 esponenziali,l’assorbimento é dato dalla somma dei 2 termini che figurano all’esponente negativo. Ciascuno dei 2 termini è dato dalla somma dei coefficienti di assorbimento pesati sulla concentrazione relativa dei diversi elementi, rispettivamente, all’energia E0 per la radiazione di eccitazione, e all’energia Ei per quella caratteristica. I fattori 1/sinψ1 e 1/sinψ2, sono introdotti per tenere conto dell’inclinazione rispetto alla superficie. Il risultato della integrazione su x rappresenta l’intensità xrf del generico elemento i .
Per un pellet che abbia spessore finito x0 si ottiene: (cfr. anche figura 6).
Per i metalli, lo spessore del campione può essere considerato infinito ai fini dell’assorbimento della radiazione X , se superiore al decimo di mm. Nel caso di uno spessore infinito, l’integrazione fornisce il risultato seguente (v. anche figura 7).
Si noti che abbiamo definito lo spessore equivalente di un campione di spessore infinito come quello dato dall’inverso del coefficiente di assorbimento totale, cioè dell’inverso della somma del coefficiente nel percorso di entrata alla energia E0e di quello nel percorso di uscita, alla energia Ei.
Può essere utile a chiarirne il significato considerare, per confronto, il caso di un cilindro di materiale radioattivo omogeneo, anche esso di spessore infinito. Il cilindro contiene un elemento radioattivo diffuso uniformemente nel suo volume che genera radiazione X . L’intensità della radiazione misurata alla superficie piana del cilindro, a parte termini di efficienza di conteggio, é data dal prodotto dell’intensità per unità di spessore moltiplicata per lo spessore equivalente. In questo caso, lo spessore equivalente é pari all’inverso del coefficiente di assorbimento della radiazione X prodotta nel materiale stesso. Cioè, l’auto assorbimento è quello subito dalla radiazione nel percorso di uscita verso l’esterno. Nel caso dell’analisi xrf, prima considerato, il coefficiente di assorbimento totale è dato dalla somma di quello della radiazione di eccitazione in entrata con energia E0 e di quello della radiazione caratteristica in uscita di energia Ei .
Il problema dell’analisi quantitativa che si incontra, in pratica, dipende dalla difficoltà di valutare con adeguata precisione l’intensità della radiazione di eccitazione incidente, il fattore di efficienza geometrica e quello di efficienza intrinseca del rivelatore.
Si considera allora, nel cosiddetto metodo dei parametri fondamentali, l’intensità I(i) emessa da un campione puro (standard di riferimento, con ci=1) con la stessa forma di pellet e nelle stesse condizioni sperimentali di misura. L’intensità emessa dallo standard di riferimento é data da:
Nel rapporto sperimentale Ri, di intensità , fra campione e standard, si eliminano i fattori in comune difficilmente calcolabili. Il rapporto è dato da (cfr. anche figura 9):
Cioè il rapporto fra Ii e l’intensità del campione di concentrazione unitaria I(i) vale esattamente il valore di ci corretto per il rapporto dei rispettivi spessori equivalenti calcolati dai parametri di assorbimento atomici noti dalla letteratura scientifica.
In definitiva, partendo dalla misura delle n righe di fluorescenza relative agli n elementi rivelati, l’analisi xrf fornisce un sistema di n equazioni lineari omogenee dipendenti nelle concentrazioni ci , la cui soluzione è definita a meno di una costante determinata dalla condizione di normalizzazione:
Si noti che nel caso che si impieghi un anodo secondario per generare la radiazione di eccitazione, la stessa approssimazione di trascurare la presenza della riga Kβ ,accanto alla riga Kα , è adottata sia per il campione che per lo standard. (Inoltre, si ricordi che, in generale, l’energia della riga Kβ è molto prossima a quella della riga Kα e ha intensità inferiore al 20% .) Perciò, l’approssimazione di considerare la radiazione di eccitazione monocromatica di energia pari a quella della riga Kα non produce, in pratica, alcun errore sulla concentrazione relativa ci ricorrendo al rapporto di intensità emesse dal campione e dallo standard.
Come illustrato nella figura 9, che rappresenta in scala logaritmica il caso del tungsteno (W), elenchiamo i parametri atomici fondamentali caratteristici della emissione xrf dell’atomo:
Si osservi che, tuttavia, ricorrendo al confronto con uno standard di riferimento tali parametri non compaiono nelle equazioni per la determinazione delle concentrazioni relative.
La formula finale per l’analisi quantitativa nel caso di eccitazione monocromatica può essere riscritta sinteticamente indicando i coefficienti di assorbimento totale della matrice alle diverse energie nel modo seguente (cfr. anche figura 10):
Introducendo le ulteriori quantità (v. anche figura 11):
definendo per la coppia di elementi i e j , il rapporto
e tenendo conto, infine, della condizione di vincolo:
si ricavano le relazioni seguenti( omettendo di indicare che i calcoli si riferiscono alla energia di eccitazione E0 )
dove:
e quindi si ottiene (cfr. anche figura 12):
Dove bij è il coefficiente di influenza relativa attribuito alla presenza dell’elemento j sulla misura dell’intensità XRF dell’elemento i (con radiazione di eccitazione di energia E0) .
Un valore del fattore di influenza pari a 0 ( ovvero: αij=1), indica che la presenza dell’elemento è ininfluente nella determinazione della concentrazione relativa di i ,ricorrendo al metodo di confronto con l’intensità di fluorescenza caratteristica dallo standard di riferimento con concentrazione unitaria.
Supponendo che tutti i coefficienti bij abbiano valore nullo, la relazione Ri=ci ha il significato ovvio di fornire una prima valutazione approssimativa della concentrazione relativa dell’elemento.
Riassumendo: limitandoci al caso della eccitazione monocromatica, per le concentrazioni relative si ottiene un sistema di n equazioni lineari omogenee dipendenti alle quali si aggiunge la condizione di chiusura ad 1 per la somma delle concentrazioni relative. La condizione di dipendenza tra le equazioni ammette l’esistenza di un set di - soluzioni, ci, diversi da quelli del caso banale nel quale siano tutti nulli. Se si ricorre alla rappresentazione con i coefficienti di influenza βij si ottiene un equivalente sistema di equazioni non omogenee nelle concentrazioni c1,…,cn .
Nell’approssimazione estrema in cui i coefficienti di influenza siano trascurati( cioè siano posti eguali a 0), si adotta l’approssimazione che l’effetto di autoassorbimento sia lo stesso per la radiazione di eccitazione e per le righe di fluorescenza caratteristica nel campione in esame e nello standard puro di ogni elemento i.
Ai fini di migliorare la comprensione del significato di questa rappresentazione del problema, consideriamo il caso di un elemento minoritario di elevato Z in una matrice composta da restanti elementi che hanno coefficienti di assorbimento, tra loro confrontabili, di valore molto minore da quello dell’elemento minoritario.
In tale caso,assumendo che i coefficienti di assorbimento degli elementi leggeri abbiano valore trascurabile rispetto quello dell’elemento pesante, dalle formule precedenti si ottiene:
ci@ 1. Questo risultato si spiega considerando che la matrice leggera del campione influenza trascurabilmente la misura della fluorescenza X dell’elemento di Z elevato e, che,per questo, lo spessore equivalente del campione ,dal punto di vista della misura della fluorescenza X, è, in pratica, lo stesso che quello dello standard puro di elemento pesante di confronto
Consideriamo, invece, il caso di un elemento leggero in una matrice composta da elementi pesanti. Questo è il caso nel quale l’eccitazione secondaria, cioè quella prodotta dalla emissione X emessa dagli elementi pesanti della stessa matrice, non è trascurabile. Avremmo, quindi, una grande correzione da apportare al valore del rapporto Ri fra la intensità di fluorescenza dal campione e dallo standard di confronto di elemento leggero puro, come sarà discusso in dettaglio in seguito.
Nel caso delle matrici leggere (Vetri, Ceramiche,per esempio) che sarà trattato a in seguito, l’effetto di auto assorbimento della matrice, che é composta da elementi leggeri non rivelabili con analisi XRF a dispersione di energia, è determinato ricorrendo a misure aggiuntive di diffusione della radiazione X di eccitazione.
Analisi di leghe metalliche e standard organici NBS
In figura 13 si riporta lo schema di un sistema sperimentale da banco di analisi xrf con anodi secondari intercambiabili, realizzato negli anni '80 nel laboratorio di archeometria del Dipartimento di Fisica dell’Università degli Studi di Milano.
Un esempio di risultati di pionieristiche analisi quantitative xrf per alcune leghe metalliche di composizione certificata è mostrata nella prima tabella di figura 14. Nella seconda sono riportate analisi di standard di campioni organici di riferimento forniti dal NBS (National Bureau of Standards) di Washington. In questo caso, l’analisi è riferita a elementi in tracce.
Monetazione antica
Il secondo esempio riguarda una serie di esemplari di monetazione arcaica in lega oro-argento (electron) del museo archeologico di Milano. Le monete hanno forma del tutto irregolare (figura 15). Ciò pone, a priori, un problema per l’applicazione del metodo di analisi xrf quantitativa basato sul confronto con standard di oro e di argento puri che abbiano superficie piana. Tuttavia, è ragionevole assumere che il fattore correttivo per l’intensità sperimentale dovuto alla superficie irregolare sia la stesso per tutte le righe X nel caso di un oggetto di composizione omogenea, cioè, che la irregolarità della superficie, che per una moneta, in generale, può anche essere data dalle raffigurazioni superficiali e dalle scritte, non modifichi le intensità delle righe X in valore relativo.
In linea di principio, il fattore costante per tutti gli elementi potrebbe essere valutato sperimentalmente ricorrendo al confronto della intensità XRF da un calco in metallo vile della moneta, ad esempio, di stagno con uno standard piano dello stesso metallo.
Più semplicemente, l’analisi può essere basata sui valori relativi delle intensità. Ciò può essere realizzato basandosi su i rapporti di intensità fra coppie di righe, scegliendone, per esempio, una come riferimento e, eventualmente, ripetendo la procedura cambiando la riga, come riscontro dell’affidabilità del metodo. La complicazione deriva dal fatto che il rapporto delle equazioni lineari corrispondenti a due righe X genera un’equazione di secondo grado e la soluzione del sistema di equazioni non lineari deve essere trovata con metodo numerico.
Si noti che, nel caso generale che l’eccitazione della fluorescenza caratteristica sia polienergetica, le equazioni per le intensità delle righe X non sono più lineari. Come sarà discusso in seguito, nell’attuale codice Axil, distribuito dalla Iaea (International Agency of Atomic Energy) la soluzione numerica del problema è ottenuta a partire dalle intensità relative (cioè dal valore di intensità di ciascuna riga diviso per la somma delle intensità di tutte le altre). Questo metodo di soluzione ha il vantaggio aggiuntivo di eliminare l’eventuale presenza di un fattore correttivo costante, dovuto alla forma irregolare.
Empiricamente, ricorrendo alla rotazione, durante la misura, della moneta attorno a un asse ortogonale alla superficie, si possono mediare e ridurre gli effetti dovuti all’irregolarità della superficie stessa. Con procedura più semplice, nella condizione che nel sistema sperimentale si abbia per gli angoli la condizione ψ1 = ψ2 , si può ottenere lo spettro di fluorescenza X corrispondente alla sovrapposizione di due misure, eseguite con lo stesso tempo di irraggiamento, nelle due giaciture opposte della moneta ottenute con una rotazione di 180 ° sul piano di riferimento (figura 16). In questo metodo,ciascun elemento di superficie orientato con un dato angolo rispetto la verticale alla superficie ideale piana nella prima misura, verrà ad assumere nella seconda misura, nella posizione ruotata di 180° sul piano, una inclinazione con angolo, rispetto la verticale, eguale ma di segno opposto. Così, il valore effettivo della correzione per la superficie irregolare si riduce al valore medio delle due misure, che può considerarsi molto piccolo.
Nella stessa figura 16 il primo ingrandimento evidenzia che alcune zone risultano schermate (effetto di overshadowing) rispetto alla radiazione di eccitazione e/o di emissione. Nel secondo ingrandimento, è messo in evidenza che gli angoli effettivi dei singoli elementi di superficie analizzata variano da punto a punto. Cioè nel caso che l’oggetto abbia una forma irregolare, gli angoli di irraggiamento e di rivelazione effettivi sono diversi da quelli fissati dalla geometria per un oggetto piano, e diversi fra di essi. Il ricorrere alle intensità relative non elimina, se non con buona approssimazione, l’effetto della forma irregolare.
Se si esegue la misura come somma degli spettri xrf in due giaciture opposte ottenute con la rotazione di 180° e il sistema è realizzato con disposizione geometrica simmetrica ψ1 = ψ2 , (ma non necessariamente con entrambi gli angoli di 45°), si può praticamente eliminare la dipendenza del risultato dagli angoli.
Nella tabella di figura 17 sono riportati esempi di risultati, dell’analisi xrf della monetazione arcaica nella ipotesi che la modifica, dovuta alla forma irregolare, del rapporto dell’intensità rispetto a quella del campione piano di concentrazione unitaria, sia la stessa per le righe X di ogni elemento.
Il rapporto fra il valore della densità corrispondente alla composizione determinata dall’analisi xrf (ρXRF) e quello ottenuto per mezzo della pesata in acqua distillata (ρSG), riportati separatamente, è indicato nell’ultima colonna della tabella.
In quanto al problema della soluzione numerica del sistema di equazioni non lineari generato nel caso che l’ eccitazione sia policromatica, l’ argomento sarà ripreso in particolare, nel caso di oggetti metallici di forma irregolare. Vedremo che il valore della precisione nella analisi xrf quantitativa non dipende dalla approssimazione nella valutazione del fattore correttivo per la forma irregolare dell’oggetto, ma dal fatto che si assume che questo fattore sia indipendente dalla energia della radiazione X .
L’effetto dell’eccitazione secondaria consiste nel fenomeno nel quale la radiazione X emessa dagli elementi maggioritari della composizione del campione eccita la fluorescenza X degli elementi leggeri. L’intensità di eccitazione secondaria è rilevante in rapporto a quella primaria, per esempio, per gli elementi leggeri minoritari contenuti nelle leghe metalliche di elementi pesanti.
In figura 18 è rappresentato lo spettro di intensità di emissione X del ferro dovuta alla eccitazione secondaria prodotta dal nichel in una lega Ni-Fe . Si assume che la radiazione di eccitazione primaria sia quella di un tubo X . Si noti che nella rappresentazione si è utilizzata la lunghezza d’onda della radiazione X non l’energia.
Il contributo all’eccitazione del ferro, dovuto alla emissione primaria XRF del nichel, è limitato alle lunghezze d’onda nello spettro del tubo minori di un dato valore massimo (i.e. a l’energia maggiore del valore che abbiamo già chiamato di absorption edge)caratteristico del nichel. In corrispondenza di questo valore di lunghezza d’onda, l’intensità della fluorescenza X del ferro subisce una diminuzione a gradino a causa dell’ aumento, anche esso a gradino, dell’ assorbimento, dovuto al nichel, della radiazione di prodotta dal tubo. In corrispondenza di questo stesso valore di lunghezza d’onda, inizia l’effetto di eccitazione secondaria del ferro da parte del nichel. Si noti che, nel caso specifico rappresentato per una lega nichel- ferro , il contributo dell’eccitazione secondaria è confrontabile con il contributo dell’eccitazione primaria. In generale, trascurare l’eccitazione secondaria nell’analisi delle leghe metalliche produce un notevole errore nell’analisi quantitativa.
La figura riporta anche il caso di eccitazione terziaria; tuttavia l’eccitazione terziaria non ha di solito importanza.
Calcolo dell’eccitazione secondaria
Cominciamo col calcolare l’eccitazione secondaria nel caso di eccitazione primaria monocromatica di energia E0. Assumiamo che un generico atomo , j , di Z elevato collocato alla profondità x1 emetta la sua fluorescenza caratteristica di energia Ej nella direzione θ e essa produca l’eccitazione secondaria di un generico atomo, i , di minore Z, che si trova alla profondità x2 . Siano cj e ci le concentrazioni relative rispettive.
Per calcolare l’intensità di’eccitazione secondaria in totale emessa dal campione, dobbiamo eseguire un integrale di volume esteso a tutto il campione. Manteniamo la condizione che gli angoli rispetto la superficie del campione della direzione della radiazione di eccitazione e di quella di rivelazione della fluorescenza X siano costanti in tutto il volume esaminato.( Come già notato,ciò significa in pratica che i valori di spessore e di estensione della zona irraggiata sono trascurabili in confronto alle distanze dal campione del tubo X e del rivelatore). L’integrazione riguarda allora solo le variabili indipendenti x1 , x2 , θ. L’elemento dell’ integrale in queste variabili è raffigurato nella figura 19. In questa è rappresentata l’emissione fra le direzioni θ e θ+dθ dei raggi X di energia Ej, prodotti da un atomo j , contenuto nello strato dx1 alla profondità x1,. Essi generano l’eccitazione secondaria dagli atomi leggeri i , contenuti nell’elemento di volume circolare di spessore dx2 , alla profondità x2 ,prodotto dall’intersezione dello spessore dx con i coni di semi apertura θ e θ + dθ . Nel calcolo della intensità secondaria dell’elemento i deve essere introdotta l’attenuazione subita dai raggi X emessi dagli atomi j lungo il percorso (x2–x1)/cos θ all’interno del campione.
La rappresentazione di figura 19 per motivi di chiarezza, non è in scala. In effetti, le distanze percorse dai raggi X all’interno di un campione metallico sono, come nel caso della eccitazione primaria, trascurabili rispetto alle distanze del tubo X e del rilevatore dalla superficie del campione. Pertanto, l’intero volume di integrazione è da considerarsi microscopico e si ha in conclusione un fattore di efficienza geometrica identico a quello dell’eccitazione primaria.
In formule, il contributo all’eccitazione secondaria della fluorescenza caratteristica degli atomi i, dovuta all’emissione degli atomi j , generato nell’elemento di volume infinitesimo di figura, per un generico valore delle variabili x1 , x2, θ , e per i valori di concentrazione relativa ci, cj è dato da:
Il fattore geometrico G , come già detto, è lo stesso che per l’eccitazione primaria. Nella formula figurano:
Come già notato, l’attenuazione totale nel processo di eccitazione secondaria è data, oltre che dal prodotto delle attenuazioni all’ingresso e all’uscita, rispettivamente, alle energie E0 e Ei , che figura anche nella eccitazione primaria, dal termine di attenuazione della radiazione emessa dall’atomo j all’energia Ej calcolato per la distanza |x2 –x1| / cos θ fra gli atomi j e i che é data dal valore assoluto del termine (x2 – x1) / cosθ .
Per non appesantire la scrittura abbiamo indicato con μM il coefficiente di assorbimento della matrice intendendo che sia dato dalla somma dei coefficienti dei singoli elementi della composizione pesati dalle concentrazioni relative.
L’integrale triplo sulle variabili x1 , x2 , θ , determina il contributo totale alla eccitazione secondaria I'i. Cioè (cfr. anche figura 20):
Il calcolo di questo integrale, assumendo che la radiazione di eccitazione sia monocromatica di energia E0 , si esegue nelle tre variabili indipendenti x1, x2, θ . In modo del tutto analogo che per l’eccitazione primaria, l’angolo solido del rivelatore si assume costante ,così pure gli angoli ψ1 e ψ2 sono considertai costanti su tutto il volume analizzato
L’integrazione ha soluzione analitica solo nell’approssimazione che lo spessore esaminato sia infinito. Si noti che questa condizione non è in contraddizione con quella che gli angoli di irraggiamento e di rivelazione siano costanti, poiché uno spessore, che può essere considerato infinito in un metallo dal punto di vista dell’assorbimento della radiazione X, è di valore trascurabile rispetto alle distanze, già citate, dalla superficie del campione del tubo X e del rilevatore.
Poiché la distanza percorsa lungo la direzione determinata dall’angolo θ si calcola con il valore assoluto della differenza x2-x1, ciò implica una inversione di segno nei 2 semispazi indicati nella figura. Conviene considerare l’integrale come somma di 2 contributi relativi, rispettivamente, al semispazio al di sopra della quota x2 (ovvero per x1 < x2 ) e al semispazio inferiore (ovvero per x1 > x2 ) e calcolare i 2 integrali separatamente. L’integrale per il calcolo della eccitazione secondaria totale può essere scritto nella forma seguente nella quale figurano separatamente i doppi integrali sulle variabili x1 e x2 da calcolare nei due semispazi (cfr. anche figura 21):
Si precisa (cfr. figura 19) che si ha una diversa definizione dell’angolo θ nei due semispazi.
Calcoliamo l’ integrale corrispondente al contributo dal semispazio inferiore. Abbiamo la semplice sequenza di calcoli che segue (cfr. anche figura 22):
Infine l’integrazione sulla variabile θ fornisce (cfr. anche figura 23):
Se si procede allo stesso calcolo per il contributo dalla zona superiore (ovvero per x1 < x2 ) compare come estremo inferiore di integrazione su x1 il valore 0, ( mentre ∞ compare come estremo superiore per x1 nella zona inferiore) ciò produce una procedura per ottenere l’integrazione molto più lunga. Si ottiene, comunque, un risultato simmetrico di quello del semispazio inferiore, nel senso che si scambiano coefficiente di assorbimento e angolo di irraggiamento della radiazione di eccitazione incidente con coefficiente di assorbimento e angolo di rivelazione della radiazione caratteristica emessa dall’elemento i .Ciò è del tutto ragionevole, perché se scambiamo l’ordine di integrazione su x1 e su x2 si ottiene nel semispazio superiore una situazione del tutto analoga a quella del semispazio inferiore, con l’unica condizione di scambiare fra loro radiazione di eccitazione e radiazione di emissione e, d’altro canto, l’effetto dell’assorbimento dipende solo dallo spessore attraversato e non dal fatto che la radiazione sia entrante o uscente in una stessa direzione.
In definitiva, possiamo introdurre per il calcolo della eccitazione secondaria il termine relativo all’elemento pesante j Aij(cfr. anche figura 24):
Che ha una struttura simmetrica in 2 termini identici: nel primo figura energia e angolo della radiazione di eccitazione, nel secondo: energia e angolo della radiazione emessa.
Allora,per la fluorescenza prodotta in totale (primaria + secondaria) si ha:
dove il termine relativo alla eccitazione secondaria dall’elemento j vale:
e, come già visto:
Mentre per Dijsi ha
![]()
:
![]() Infine, si é fatto uso della notazione:
Infine, si é fatto uso della notazione:
Φ1 ≡ cosec ψ1
Φ2 ≡ cosec ψ2
La produzione xrf totale è data,dunque, da un’unica espressione che include sia l’eccitazione primaria, sia i diversi contributi di eccitazione secondaria dovuta ai diversi atomi più pesanti esistenti nel campione. Poiché l’effetto di eccitazione secondaria non è trascurabile solo se l’atomo pesante responsabile è presente in rilevante concentrazione, non si dà mai, in pratica, il caso che i termini dalla sommatoria su j siano più di 2 o 3
Si noti che il termine μi(E0) a dividere nel fattore δij è introdotto solo per ottenere un unico fattore moltiplicativo in evidenza nella formula per l’intensità xrf totale.
La dipendenza aggiuntiva dagli angoli della intensità di fluorescenza prodotta dovuta alla eccitazione secondaria è molto piccola (cfr. anche figure 25 e 26).
Nel primo dei due termini che figurano in Aij , la condizione
è sicuramente verificata, essendo E0 > Ej . Quindi il primo termine in Aij si riduce a 1 / μM(Ej) , poiché si può assumere l’approssimazione ln (1+x) ≈ x
Si noti, invece, che nel secondo termine la condizione opposta:
é verificata poiché Ei è minore di Ej . Si può, comunque, tenere per buona l’approssimazione opposta a questa al solo scopo di rendere più chiaro il significato della espressione matematica ottenuta per l’eccitazione secondaria.
Introducendo entrambe le approssimazioni precedenti in Aij, , il risultato dell’integrazione che determina il contributo dell’eccitazione secondaria nel temine δij si riduce semplicemente a 1 / μM(Ej) .
Per ottenere questo risultato, consideriamo l’eccitazione secondaria generata alla distanza R dal punto, di origine della radiazione di energia Ej , cioè dall’atomo dell’elemento j , consideriamo che l’emissione sia isotropica. Essa è data:
Ricordando che la concentrazione ci relativa degli atomi i figura a moltiplicare nella formula già ottenuta ,si ha che il contributo dell’eccitazione secondaria dipende dal termine:
Integrando su R da 0 a ∞ si ottiene immediatamente (cfr. anche figura 27):
(dove si é fatto uso della relazione:
Questo risultato si può interpretare rappresentando con una sfera di raggio 1 / μM(Ej) lo spazio intorno a ogni atomo j nel quale si genera l’eccitazione secondaria. Il volume della sfera è molto più piccolo del volume del campione analizzato così da rendere valida l’approssimazione che gli angoli ψ1, ψ2 siano costanti.
Il termine μj(E0) , cioé il coefficiente fotoelettrico alla energia E0 dell’atomo j, responsabile della fluorescenza secondaria, moltiplicato per il rapporto ![]() (ottenuta con l’approssimazione ln (1+x )@ x ) ulteriormente moltiplicato per il fattore atomico Pj, rappresenta approssimativamente il termine che abbiamo chiamato dij nelle formule precedenti, cioé il fattore che determina il contributo alla eccitazione secondaria dell’atomo i dovuto alla presenza dell’ atomo j.
(ottenuta con l’approssimazione ln (1+x )@ x ) ulteriormente moltiplicato per il fattore atomico Pj, rappresenta approssimativamente il termine che abbiamo chiamato dij nelle formule precedenti, cioé il fattore che determina il contributo alla eccitazione secondaria dell’atomo i dovuto alla presenza dell’ atomo j.
Il risultatodi queste considerazioni è che il fattore che misura l’aumento di intensità di fluorescenza dovuto alla eccitazione secondaria non dipende dal valore dell’angolo di ingresso, poiché la condizione μjM(E0)<< μM(Ej) é sicuramente verificata. Mentre la condizione μjM(Ej)<<μM(Ei) non è vera. Pertanto si conserva una debole dipendenza dall’angolo di emissione ψ2 per l’ eccitazione secondaria.
.
Analisi quantitativa
Anche in presenza dell’eccitazione secondaria, l’analisi quantitativa è basata sul confronto con uno standard di riferimento di composizione unitaria.
Si ha quindi (cfr. anche figura 28) il sistema di equazioni:
Si ricorda che si sono già definiti:
e, poiché vale la condizione:
si ha infine (cfr. anche figura 29):
In definitiva, scriviamo l’elegante equazione:
(Si ricordi che ( nell’approssimazione di trascurare la dipendenza dagli angoli appena discussa):
dove Aij è il risultato calcolato precedentemente dell’integrazione sulle tre variabili x1 , x2 , θ ).
Per i coefficienti di influenza βij e i coefficienti δij ricavati per l’eccitazione secondaria si é trascurato di indicare che dipendono anche dalla energia di eccitazione E0 Si noti che nell’approssimazione estrema di considerare i coefficienti di influenza e i contributi di eccitazione secondaria trascurabili (cioè, tutti i coefficienti βij e δij nulli) si avrebbe, ovviamente ci = Ri . Cioè il rapporto dell’intensità xrf con quella del campione di i puro fornirebbe la misura della concentrazione relativa dell’elemento i nel campione in analisi fortemente approssimata avendo trascurato sia la correzione per l’autoassorbimento della matrice che l’eccitazione secondaria.
Come ultima nota, aggiungiamo che nella formula finale potremmo estendere le sommatorie a tutti i valori di j senza l’esclusione del valore j= i. In tale caso infatti si ha che entrambi i coefficienti βij ee δij hnno valore nullo.
Fonte: http://www2.fisica.unimi.it/milazzo/MetodiFisicaApplicata_cap4_AnalisiXrfMonocromatica%20AA2011%202012.doc
Sito web da visitare: http://www2.fisica.unimi.it
Autore del testo: non indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve