

I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Lo stato di aggregazione di una sostanza, solido, liquido o aeriforme, dipende, oltre che dal tipo e dall'intensità delle forze intermolecolari, dai valori che assumono la pressione P, la temperatura T ed il volume V. Per questo motivo tali grandezze sono dette variabili di stato.
Nello stato gassoso le distanze tra le molecole risultano molto elevate, poiché le particelle possiedono energia cinetica sufficiente a vincere le forze di attrazione intermolecolari e sono perciò in grado di separarsi. Il moto caotico delle particelle allo stato gassoso determina il fenomeno della diffusione, per il quale un gas occupa sempre tutto lo spazio a sua disposizione e presenta per questo motivo forma e volume del recipiente che lo contiene.
Il Volume è definito come la porzione di spazio occupata da un corpo. Esso viene misurato in m3 ed in chimica, più spesso in litri (L).
La Temperatura misura la capacità di un corpo di dare sensazioni di caldo e freddo. Più precisamente essa è una misura dell'energia cinetica media delle particelle che costituiscono un corpo.
La temperatura si misura in
1) gradi centigradi o Celsius (°C)
2) gradi assoluti o Kelvin (K)
3) gradi Fahreneit (°F).
La scala Celsius (t) è convenzionalmente costruita assegnando al ghiaccio fondente la temperatura di 0 °C e all'acqua bollente la temperatura di 100 °C.
La scala delle temperature assolute (T) è costruita partendo dalla constatazione che la più bassa temperatura Celsius corrisponde a -273,15°C. Poiché non sono possibili temperature inferiori, tale valore rappresenta lo zero assoluto delle temperature.
La scala delle temperature assolute si ottiene quindi traslando l'origine della scala Celsius dagli 0°C a -273,15°C.
E' evidente quindi che per trasformare i gradi Celsius in gradi Kelvin è sufficiente utilizzare la seguente relazione di conversione
T = t + 273,15
Così, ad esempio, lo zero della scala Celsius corrisponde a 273,15 K, mentre l'acqua bolle a 373,15 K.
Nella scala Fahreneit al ghiaccio fondente è assegnata convenzionalmente una temperatura di 32 °F, mentre all'acqua bollente è assegnata convenzionalmente la temperatura di 212 °F . A differenza della scala centigrada dunque, dove tale intervallo è diviso in 100 gradi, nella scala Fahreneit è suddiviso in 180 gradi. Un grado Fahreneit risulta perciò più piccolo di un grado centigrado. |
La temperatura determina la direzione del flusso di calore.
La Pressione si definisce come il rapporto tra una forza e la superficie sulla quale la forza agisce.
Le unità di misura della pressione sono molteplici. Le più utilizzate sono
a) Chilogrammo su centimetro quadrato (kg/cm2)
b) Atmosfera (atm). E' definita come la pressione esercitata dall'atmosfera terrestre sul livello del mare (slm), a 0°C, a 45° N, con un'umidità relativa pari allo 0% .
1 atm = 760 mm di Hg ( o torr) = 1,033 kg/cm2
c) Pascal (Pa). Nel Sistema Internazionale SI è la forza esercitata da 1 N (newton) sulla superficie di m2. ( 1 newton è la forza che, applicata alla massa di 1 Kg produce un'accelerazione di 1 m/s2).
d) Bar. Nel sistema cgs è la forza esercitata da 106 dine su 1 cm2. ( 1 dina è la forza che, applicata alla massa di 1 g produce un'accelerazione di 1 cm/s2).
1 atm = 1,013 Bar = 101.300 Pascal
Si definiscono condizioni normali (c.n.) o standard di temperatura e pressione (STP), la temperatura di 0 °C e la pressione di 1 atm.
Le ricerche sperimentali effettuate sullo stato aeriforme (a partire dai lavori di Robert Boyle verso la metà del Seicento) hanno dimostrato che se un gas è sufficientemente rarefatto e/o possiede una temperatura sufficientemente elevata, il suo comportamento fisico risulta indipendente dalla sua natura chimica. In altre parole, tutti i gas che si trovano sufficientemente distanti dal loro punto di liquefazione si comportano allo stesso modo e possono essere descritti mediante un unico formalismo matematico.
E' cioè possibile trattare le particelle che compongono il gas (molecole o atomi che siano) come punti materiali le cui interazioni dipendono esclusivamente dal loro numero per unità di volume e dalla loro energia cinetica media, trascurando le forze intermolecolari che dipendono evidentemente dalla loro natura chimica.
Tale approccio verrà in effetti completamente sviluppato e formalizzato solo nella seconda metà dell'Ottocento con la Meccanica statistica, attraverso la teoria cinetico- molecolare dei gas.
E' comunque possibile descrivere il comportamento fisico dei gas senza ricorrere ad una descrizione della dinamica delle interazioni molecolari, limitandosi a formulare le relazioni che legano le variabili macroscopiche o variabili di stato: pressione, volume e temperatura.
Tali relazioni sono note come leggi dei gas perfetti.
Un gas perfetto è un gas ideale in cui gli urti delle particelle sono perfettamente elastici, ciascuna particella non occupa virtualmente volume (particella puntiforme) e non vi sono forze intermolecolari che vincolino in alcun modo il moto delle molecole. E' evidente che un gas perfetto in realtà non esiste, si tratta solo di un'utile astrazione. Ma in opportune condizioni di rarefazione i gas reali possono avvicinarsi in modo accettabile a tale modello ideale.
Le leggi dei gas perfetti sono 4. Le prime tre sono state ottenute mantenendo costante una delle tre variabili di stato ed osservando sperimentalmente la relazione esistente nelle variazioni delle due rimanenti. La quarta legge mette invece in relazione contemporaneamente tutte e tre le variabili di stato in un'unica equazione.
(relazione tra P e V con T costante)
Nel 1662 Boyle dimostrò che mantenendo costante la temperatura il volume di una data massa di gas è inversamente proporzionale alla pressione esercitata su di esso.

P1.V1 = P2.V2 = K
ed in definitiva
PV = K
La curva che si ottiene ponendo in ascisse il volume ed in ordinata la temperatura è naturalmente un ramo di iperbole equilatera detta isoterma. Naturalmente effettuando l'esperimento a diverse temperature si ottengono diverse isoterme. Aumentando la temperatura l'isoterma si sposta verso l'esterno.
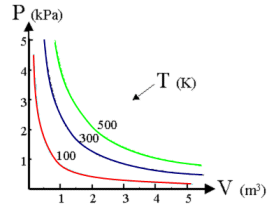
(relazione tra V e T con P costante)
Nel 1787 il francese J.A.C. Charles dimostrò che gas diversi mantenuti a pressione costante subiscono la stessa dilatazione quando vengono portati da 0°C a 100°C.
|
Nel 1802 Gay-Lussac, riprendendo le esperienze di Charles, giunge a formulare una relazione che lega il Volume alla temperatura
dove
a = è il coefficiente di espansione e vale 1/273
Vt = Volume alla temperatura di t°C
Vo = Volume alla temperatura di 0°C
In altre parole, mantenendo costante la pressione, ogni aumento di 1° della temperatura produce un aumento del volume pari ad 1/273 del volume che il gas occupava alla temperatura di 0°C.
Infatti
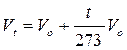
dove si osserva che il volume alla temperatura di t°C (Vt) è pari al volume alla temperatura di 0°C (Vo) aumentato di un valore pari a t/273 del volume Vo.
La relazione precedente può essere scritta
![]()
e ricordando che 273 + t = T

Poiché infine il volume a pressione costante (P = K) e alla temperatura di 0°C assume sempre lo stesso valore, il rapporto Vo/273 è una costante.
Se quindi esprimiamo la temperatura in gradi assoluti, la legge di Gay-Lussac afferma che il volume a t°C è direttamente proporzionale alla temperatura assoluta. Il valore della costante di proporzionalità dipende ovviamente dalla pressione alla quale facciamo l'esperimento e dalla quantità di gas che si prende in considerazione.
La relazione che lega il Volume alla Temperatura a Pressione costante è dunque di proporzionalità diretta ed è quindi rappresentabile tramite una retta di pendenza Vo/273.
Se in ascissa poniamo la temperatura centigrada la retta incontra l'asse delle ordinate in Vo. e quello delle ascisse in -273. Se in ascissa poniamo la temperatura assoluta la retta attraversa l'origine. La retta ottenuta è detta 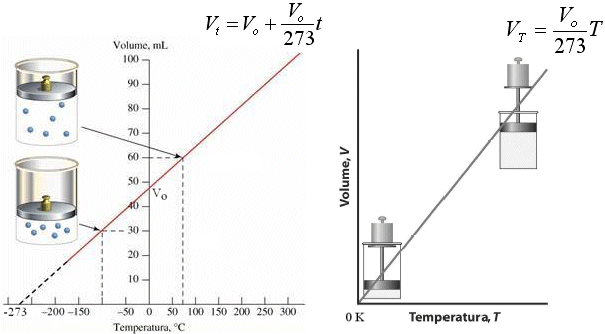
Naturalmente i valori espressi dalla retta hanno significato solo fino ad una certa temperatura, al di sotto della quale il gas si liquefa e diventa in pratica incomprimibile. Facendo comunque proseguire idealmente la retta (linea tratteggiata) si raggiunge lo zero assoluto (-273°C) al di sotto del quale si otterrebbe il risultato assurdo di un volume negativo della materia.
(relazione tra P e T a V costante)
Analogamente a quanto avviene nella prima legge di Gay-Lussac, la pressione di un gas a volume costante è direttamente proporzionale alla temperatura.
Se si utilizza la temperatura centigrada si ha
![]()
con
a = 1/273
Pt = Pressione alla temperatura di t°C
Po = Pressione alla temperatura di 0°C
In altre parole, mantenendo costante il volume, ogni aumento di 1° della temperatura produce un aumento della pressione pari ad 1/273 della pressione che il gas esercitava alla temperatura di 0°C.
Infatti
![]()
dove si osserva che la pressione alla temperatura di t°C (Pt) è pari alla pressione alla temperatura di 0°C (Po) aumentata di un valore pari a t/273 della pressione Po.
Anche in questo caso, esprimendo la temperatura in gradi Kelvin si ottiene una retta passante per l'origine, detta isocora, di equazione
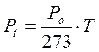

Le tre leggi dei gas possono combinarsi in un'unica relazione in cui compaiono contemporaneamente tutte e tre le variabili di stato. L'equazione è dovuta al francese Clapeyron (1834).
Si consideri 1 mole di un gas qualsiasi e le due isoterme di 0°C e di t°C.
Consideriamo ora i tre punti A, B e C posti sulle isoterme e le trasformazioni A→B e B→C
1) La trasformazione A→B, avvenendo a pressione Po costante è una trasformazione isobara per la quale vale la relazione Vt = Vo(1 + at)
2) la trasformazione B→C, avvenendo a temperatura t costante è una isoterma per la quale vale la relazione PV = PoVt.
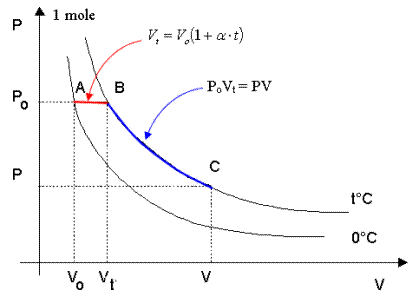
sostituendo ora nella seconda il valore Vt ricavato dalla prima si ottiene
PV = PoVo(1+ at)
da cui ![]()
e quindi ![]()
Poiché Po e Vo sono la pressione e il volume alla temperatura costante di 0°C, il loro prodotto è, per la legge di Boyle, costante e quindi anche la quantità ![]() è costante.
è costante.
Ricordando che 1 mole di qualsiasi gas a 0°C e ad 1 atmosfera occupa sempre 22,414 L, se poniamo Po = 1 atm, Vo sarà appunto pari a 22,414 L ed il rapporto, noto come costante universale dei gas R, varrà
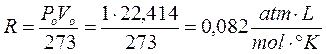
Ricordiamo che se esprimiamo la pressione in Pascal ed il volume in m3 (sistema SI) R vale
 o
o 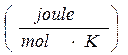
mentre nel sistema cgs R vale
![]()
Per una mole di gas l'equazione di stato diventa dunque
PV = RT
Per n moli il volume Vo ad 1 atmosfera e 0°C non sarà evidentemente 22,414 L, ma sarà pari ad n volte 22,414 L e l'equazione diverrà
PV = nRT
Il modello di gas perfetto è basato, come abbiamo visto, sulle seguenti due ipotesi:
i. Le molecole del gas sono sferette rigide puntiformi
ii. L’energia di interazione tra le molecole è nulla
Vedremo come il venire meno di queste ipotesi influenzi il comportamento di un gas reale. Per analizzare il comportamento non ideale di un gas reale si può esaminare il fattore di comprimibilità Z
![]()
Per il gas perfetto Z = 1, infatti, dalla legge generale del gas perfetto, il rapporto tra PV ed nRT è eguale ad 1.
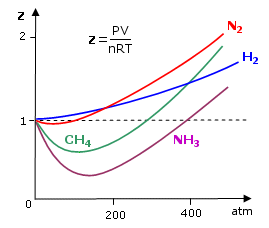
Tutti i gas reali si comportano in modo anomalo, ma tendono all'ideale (Z = 1) quando P tende a 0 e quando la loro T è alta. Per la maggior parte dei gas il rapporto di comprimibilità tende ad essere minore di 1 a basse pressioni. Questo vuol dire che quel dato gas reale è più comprimibile di quanto lo sarebbe un gas perfetto e ciò fa pensare all’esistenza di forze intermolecolari di tipo attrattivo tali da favorire la compressione del gas.
Un fattore di comprimibilità maggiore di 1 (tipicamente ad alte pressioni) è invece indice della presenza di forze intermolecolari repulsive a corto raggio d’azione tali da opporsi alla compressione.
Aumentando la temperatura i minimi delle curve diventano sempre meno marcati, finché per temperature sufficientemente elevate (il cui valore esatto dipende dal gas) il fattore di comprimibilità è sempre maggiore di 1.
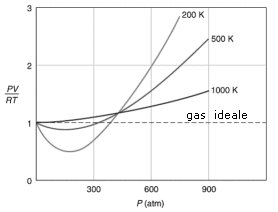
Abbiamo visto che i gas reali soddisfano l’equazione di stato del gas perfetto quando si verificano una delle due (o entrambe) le condizioni seguenti
i. Bassa densità: P → 0
ii. Alta temperatura
I gas reali non sempre si comportano idealmente, specialmente a basse temperature e/o ad alte pressioni. I motivi di questa deviazione dalla idealità sono determinati:
Van der Waals modificò l’equazione di stato del gas ideale in relazione in modo da tener conto delle due differenze essenziali fra gas ideale e gas reale:
Covolume
Se n moli di gas reale occupano il volume V, il volume in cui le molecole possono liberamente muoversi non è V ma è la differenza fra V e la parte di V materialmente occupata dall’insieme delle molecole che costituiscono le n moli. Se b è il volume materialmente occupato dalle molecole che costituiscono una mole di gas, indicato come covolume, il volume realmente disponibile per il movimento delle molecole presenti nelle n moli di gas reale è (V – nb). Il volume proprio delle molecole gassose (covolume) diventa apprezzabile in confronto al volume del recipiente quando la densità del gas in molecole per unità di volume (n/V) è elevata. Essendo n/V = P/RT, ciò si verifica ad alte pressioni e/o a basse temperature. Pertanto è:
V(ideale) = V(reale) – n×b
Forze intermolecolari
La pressione misurata sperimentalmente per un gas reale risulta sempre minore del valore ricavato dall’equazione dei gas ideali. La differenza è tanto più evidente quanto maggiore è la densità del gas, cioè ad alte pressioni e/o basse temperature.
Aumentare la pressione comporta una riduzione della distanza media tra le particelle e quindi un aumento delle forze di interazione.
Diminuire la temperatura significa rendere le molecole più lente e quindi più sensibili alle deboli forze di interazione.
Se due molecole di un gas reale vengono progressivamente avvicinate, insorgono dapprima forze attrattive, poi, al diminuire della distanza, diventano sensibili le forze repulsive che, successivamente, equilibrano e superano le forze attrattive. Nel campo di applicabilità dell’equazione di van der Waals, le distanze fra le molecole sono tali che si è sempre nel campo delle forze attrattive.
Ancora una volta, le mutue forze di attrazione intermolecolari (che vedremo più in dettaglio in seguito) diventano sensibili quando la densità del gas in molecole per unità di volume (n/V) è elevata. In queste condizioni l’affollamento è maggiore e la distanza tra le molecole minore.
Le forze di attrazione intermolecolare diminuiscono la frequenza degli urti contro le pareti del recipiente e quindi la pressione reale esercitata dal gas risulta minore di quella ideale. La coesione molecolare rallenta le molecole più esterne della massa gassosa, rendendone con ciò meno frequenti e in media meno violenti gli urti contro le pareti.
All’interno del fluido l’attrazione reciproca tra le molecole è mediamente la stessa in tutte le direzioni e quindi il suo effetto complessivo è trascurabile, mentre negli strati in prossimità delle pareti del recipiente non è così perché la compensazione viene a mancare.
Quindi per le molecole che sono in prossimità della parete si ha una forza netta diretta verso l’interno che diminuisce la pressione che avrebbe il gas in approssimazione di gas perfetto.
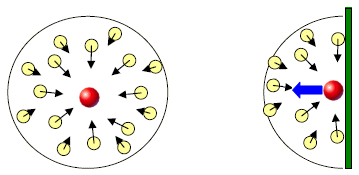
Van der Waals dimostrò che la diminuzione della pressione ideale è direttamente proporzionale al quadrato della densità del gas.
P(ideale) – a×(n/V)2 = P(reale)
Il termine a (n/V)2 è noto come pressione interna o pressione di coesione
La pressione dipende dalla frequenza di collisione con il recipiente e dall’efficacia dell’urto.
Poiché le attrazioni rallentano le molecole il loro effetto sarà duplice: le molecole colpiranno infatti le pareti del recipiente con una frequenza più bassa e con minor energia.
Entrambi gli effetti risultano proporzionali alla concentrazione del gas (n /V), pertanto la riduzione della pressione è proporzionale al quadrato della concentrazione molare.
L’equazione di stato dei gas ideali (Clapeyron)
![]()
viene dunque modificata secondo van der Waals in
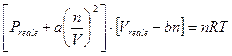
I parametri a e b sono caratteristici di ogni gas e vengono misurati sperimentalmente. Una stima del parametro b è fornita dalla misura del volume molare del composto allo stato liquido.
Si noti che, se il gas è molto rarefatto, cioè se il volume è grande, i termini correttivi introdotti diventano trascurabili e l’equazione di van der Waals tende all’equazione di stato del gas perfetto. Il valore della pressione interna è del tutto trascurabile in rapporto a quello della pressione effettiva alle normali condizioni di pressione e temperatura, non può invece essere trascurato, neanche in valutazioni di prima approssimazione, quando la pressione diventa molto grande e la temperatura molto bassa. Per aria sotto pressione di 1 atm, la pressione interna vale solo 0,0028 atm a 0°C, e 0,0056 atm a -75°C. Ma sotto pressione di 100 atm, la pressione interna vale 26 atm a 0°C, e 84,5 atm a -75°C.
Il valore del covolume, diverso da gas a gas, si aggira mediamente attorno ai 30 cm3/mol, perciò corrisponde a circa lo 0,15% del volume occupato da una mole di gas in condizioni standard di pressione e temperatura (1 atm, 0°C). Si può ritenere che il covolume corrisponda approssimativamente al quadruplo del volume complessivo delle 6,022 1023 molecole contenute in una mole.
Diagramma di Andrews
Consideriamo il comportamento dell’anidride carbonica, le cui isoterme furono determinate da T.Andrews.

A temperature elevate (> 80 ºC) le isoterme assomigliano a quelle di un gas perfetto. A temperature più basse, le isoterme cominciano a presentare un flesso, ma la pendenza continua ad essere negativa come nel resto della curva. Queste curve, si guardi quella a 40 ºC, assomigliano ad iperboli ai valori bassi della pressione (grandi volumi). A piccoli volumi si comportano diversamente. Al decrescere del volume la pressione diventa rapidamente molto grande; la curva ha un asintoto verticale, che non è, come per l’iperbole del gas ideale, l’asse delle pressioni.
Scendendo con la temperatura si incontra un’isoterma importante, che è caratterizzata dal fatto che il flesso ha tangente orizzontale. Questa isoterma si chiama isoterma critica. Il punto del flesso (K
nella figura) è il punto critico. Le sue coordinate si dicono temperatura critica Tc, pressione critica Pc e volume critico Vc .
Per l’anidride carbonica la temperatura critica vale Tc = 31.04 ºC
Scegliamo ora una temperatura più bassa delle temperatura del punto critico, ad esempio 20 ºC nel caso dell’anidride carbonica. Partiamo da un volume molto grande, cioè da pressioni relativamente basse. Diminuendo il volume si trova che la pressione del gas aumenta, fino a quando esso non raggiunge un valore ben definito (punto B della figura). A questo punto la pressione rimane costante nonostante il volume continui a diminuire. Il punto rappresentativo dello stato percorre un tratto orizzontale a pressione costante fino ad arrivare al punto A. Dopo questo punto la pressione sale bruscamente e diviene impossibile ridurre ulteriormente il volume in maniera apprezzabile. La sostanza che a volumi più grandi si lasciava facilmente comprimere è diventata praticamente incomprimibile.
Se si abbassa ulteriormente la temperatura del gas e si ripete l’operazione, si constata che il tratto orizzontale a pressione costante è divenuto più ampio. Il tratto si allunga molto dalla parte dei volumi grandi e molto poco dalla parte dei volumi piccoli.
Nel punto B inizia la liquefazione del gas. Nel tratto AB sono presenti contemporaneamente ed in equilibrio tra loro le due fasi liquide e gassose della sostanza. Ad una data temperatura questo può avvenire ad una sola pressione, chiamata la pressione del vapor saturo o tensione di vapore. Si ricava sperimentalmente che la tensione di vapore, nelle sostanze pure, dipende solo dalla temperatura e non dalla quantità di gas utilizzata nell’esperimento, vale a dire non dipende dal volume del gas.
La temperatura Tc è la massima temperatura a cui la sostanza può trovarsi nella fase liquida. A temperature maggiori la sostanza si trova solo nello stato gassoso. Seguendo una terminologia che risale ad Andrews, il termine vapore viene usato per indicare una sostanza che si trova nello stato gassoso, ma che è al di sotto della temperatura critica, ed il termine gas per indicare una sostanza gassosa al di sopra della temperatura critica.
Per temperature superiori alla temperatura di punto critico, le curve di van der Waals descrivono abbastanza bene il comportamento del gas reale, riproducendo anche la regione del flesso che non è presente nell’equazione dei gas perfetti.
Nella regione AB della transizione di fase, le curve di van der Waals non presentano il tratto orizzontale ma hanno un andamento a S che incrocia il tratto orizzontale in tre punti. In questa regione l’equazione di van der Waals perde significato fisico.
Le coordinate del flesso a tangente orizzontale dell’isoterma critica, che corrispondono alle coordinate del punto critico del gas reale, sono correlabili ai coefficienti a e b di van der Waals.
![]()
![]()
![]()
Ciò ci consente di stimare i parametri di van der Waals misurando sperimentalmente i parametri critici (Pc, Tc, Vc) di un gas.
Fonte: http://www.pianetachimica.it/didattica/documenti/Chimica_Generale.doc
Sito web da visitare: http://www.pianetachimica.it
Autore del testo: non indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve