Campo magnetico

I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Campo magnetico

IL CAMPO MAGNETICO

Forze che si esercitano in un campo magnetico sulle cariche in movimento e sulle correnti.

I fenomeni magnetici furono dapprima osservati e studiati su magneti naturali ed artificiali. Ma per capire la natura dei processi che avvengono in un magnete, bisogna dapprima studiare fenomeni più semplici e più fondamentali. Adotteremo il metodo deduttivo, ponendo alla base della nostra esposizione due risultati sperimentali ottenuti nel XIX secolo:
Il campo magnetico esercita un’azione sulle cariche in movimento;
Le cariche in movimento creano un campo magnetico.
Cominciamo con una semplicissima esperienza. Produciamo in un tubo catodico un fascio rettilineo e ben focalizzato di elettroni, che si spostano nel vuoto da sinistra a destra. Cadendo sullo schermo fluorescente il fascio lascia come traccia una piccola macchia luminosa. Avviciniamo al fascio dal basso il polo nord di un magnete rettilineo. Il fascio si sposterà lateralmente allontanandosi dal lettore. Se si avvicina al fascio il polo sud dello stesso magnete, il fascio si sposterà in senso inverso cioè avvicinandosi al lettore. Ponendo il magnete lateralmente, lo spostamento avverrà verso l’alto o verso il basso a seconda del lato dove si pone il magnete e del polo che viene avvicinato al fascio. Questo esperimento ed altri analoghi dimostrano che un elettrone in movimento è sottoposto ad una forza perpendicolare alla sua direzione di moto e alla direzione dell’asse del magnete, cioè della retta che va da uno dei poli del magnete all’altro. Questa forza è proporzionale alla velocità dell’elettrone. Analogamente si comporta qualunque altra particella carica che si muova in un campo magnetico.

La legge che definisce la forza magnetica che si esercita su una carica puntiforme q in movimento in un campo magnetico è stata ottenuta per mezzo di una generalizzazione dei dati sperimentali. Questa legge è espressa dalla formula:
(1)
dove il vettore B non dipende né dal valore della carica q né dal suo movimento. Esso caratterizza soltanto il campo magnetico nel quale si muove la carica q. Questo vettore è l’induzione magnetica. La forza magnetica è perpendicolare al vettore velocità v della particella e al vettore intensità B del campo magnetico, ed il suo valore è proporzionale al seno dell’angolo formato da questi vettori. Nei casi in cui B e v sono collineari, la forza magnetica si annulla. La formula (1) è valida non soltanto per i campi magnetici costanti ma anche per i campi variabili, qualunque sia la velocità v.
Notiamo in particolare che il campo magnetico non esercita nessuna azione sulle cariche elettriche immobili, il che costituisce una differenza sostanziale fra campo magnetico e campo elettrico. La carica nello stato di quiete serve da indicatore del campo elettrico e la carica mobile è l’indicatore del campo magnetico.
La formula (1) suggerisce un metodo di principio per la misurazione del campo magnetico B, consistente nel determinare la forza che si esercita su una carica in movimento. E’ necessario per prima cosa assicurarsi, per mezzo di una carica immobile, che non vi sia campo elettrico. Si determina poi la direzione della velocità v per la quale la forza si annulla, il che avviene quando la velocità v è parallela o antiparallela al vettore . Si sarà determinata così, a meno del segno, la direzione del campo magnetico B. Infine resta da determinare la forza che si esercita su una carica che si sposta con velocità perpendicolare al vettore B. E’, evidentemente,

Moltiplicando vettorialmente questa relazione per ed osservando che si ottiene
(2)
Questa formula definisce univocamente tanto il modulo quanto la direzione del vettore B. Che la grandezza B sia un vettore (più esattamente uno pseudovettore) risulta direttamente dalla formula (2) che rappresenta questa grandezza sotto forma di prodotto vettoriale dei vettori polari

In un campo elettrico E una carica q è sottoposta alla forza . Se i campi elettrici e magnetici agiscono sulle cariche indipendentemente, come conferma l’esperienza, sotto la loro azione simultanea una carica sarà sottoposta alla forza cioè

Questa forza si chiama forza di Lorentz..
Nell’approssimazione non relativistica la forza F, come tutte le altre forze, non dipende dalla scelta del sistema di riferimento (inerziale). Tuttavia il secondo termine della somma (3) cambia durante il passaggio da un sistema di riferimento ad un altro. Per conseguenza il primo termine qE deve cambiare anch’esso. Quindi, la decomposizione della forza totale F in forza elettrica e in forza magnetica dipende dalla scelta del sistema di riferimento. Questa decomposizione è priva di senso se non è indicato il sistema di riferimento utilizzato.

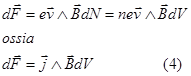
Gli esperimenti relativi all’azione esercitata dai campi magnetici sulle cariche in movimento diventano più semplici sostituendo le cariche isolate con le correnti elettriche, quando intervengono simultaneamente molte particelle cariche. Supponiamo, ad esempio, che la corrente sia dovuta al movimento di particelle identiche di concentrazione n, che portano ciascuna la carica e. Si ha allora j= nev. Il numero delle particelle contenute nell’elemento di volume dV è dN=ndV, e la forza che si esercita in un campo magnetico sull’elemento di volume dV del corpo è

Questa formula resta valida anche nel caso generale in cui la corrente passa attraverso un filo infinitamente sottile, di sezione trasversale S. Prendiamo un segmento del filo di lunghezza infinitesima dl e calcoliamo la forza dF alla quale esso è sottoposto. Se dV=Sdl è il volume di questo segmento del filo, si ha jdV=jSdl, ossia

il senso del vetore dl coincide qui con quello della corrente. Il vettore jdV è detto elemento di corrente volumetrico ed il vettoreelemento di corrente lineare. Dalle relazioni (4) e (5)si ricava
(6)
La formula (6) che definisce la forza che si esercita in un campo magnetico su un elemento di corrente lineare è stata stabilita da Ampère ed è nota come legge di Ampére. Per ottenere la forza che si esercita su un filo di lunghezza finita è sufficiente integrare la (6) su tutta la lunghezza del filo

Le forze che si esercitano sulle correnti in un campo magnetico si chiamano forze di Ampére.. Descriviamo qualche semplice esperienza dimostrativa in cui queste forze si manifestano nettamente. Prendiamo un magnete a ferro di cavallo (vedi figura) e poniamo tra i suoi poli un’asta metallica AB sospesa a due fili elettrici. Quando vi si fa scorrere una corrente continua, l’asta AB si sposta lateralmente, in un senso che la fa uscire o entrare nello spazio tra i due poli del magnete a seconda della direzione della corrente e del campo magnetico. Quando la direzione della corrente o la direzione del campo magnetico si inverte, il senso dello spostamento dell’asta si inverte.

La ruota di Barlow (1776-1862). Questo apparecchio dimostrativo si compone di un disco di rame montato su un asse orizzontale attorno al quale può ruotare (vedi figura). Il bordo inferiore del disco è immerso in una vaschetta riempita di mercurio. L’asse del disco e la vaschetta sono collegati ad una sorgente elettrica. Si pone il disco tra i poli di un magnete perpendicolarmente al campo magnetico. Quando si applica una tensione continua, una corrente radiale scorre attraverso il disco e le forze di Ampère applicate al disco lo mettono in rotazione. Quando il senso della corrente si inverte, il senso di rotazione del disco si inverte.

Questi esperimenti dimostrano che i magneti esercitano un’azione sulla corrente elettrica. Anche le correnti esercitano un’azione sui magneti. Un esempio ne è dato dal celebre esperimento di Oersted (1777-1851). Oersted dispose al di sopra di un ago magnetico un filo rettilineo parallelo all’ago. Questo poteva ruotare liberamente attorno ad un asse verticale. Quando si faceva passare una corrente elettrica nel filo, l’ago veniva deviato e si disponeva in una posizione perpendicolare al filo. Quando si invertiva il senso della corrente, l’ago ruotava di 180°. Si osservano i medesimi effetti quando si disponeva il filo elettrico al di sotto dell’ago magnetico. L’esperimento di Oersted, realizzato nel 1820, permise per la prima volta di stabilire un legame tra i fenomeni elettrici e quelli magnetici.

Campo magnetico di una carica in moto uniforme. Legge di Biot e Savart.

Enunciamo ora la legge che determina il campo magnetico creato da una carica puntuale q in movimento, limitandoci al caso di moti uniformi a bassa velocità. La legge è stata stabilita generalizzando i dati sperimentali ed è espressa dalla formula

dove r è il raggio vettore condotto dalla carica q al punto di osservazione. Il campo elettrico di una carica immobile della stessa grandezza q e nello stesso punto di osservazione è determinato dall’espressione

Quindi

ossia

Utilizziamo queste formule per il calcolo della forza di interazione di due cariche puntuali in movimento. Questa interazione si compone di una interazione elettrica (secondo la legge di Coulomb) e di una interazione magnetica. In ciò che segue tratteremo solo l’interazione magnetica. Siano le velocità delle cariche in movimento. L’intensità del campo magnetico creato dalla carica q(1) nel punto dove si trova la carica q(2) è

dove è il raggio vettore condotto dalla prima carica alla seconda. Questo campo esercita sulla carica q(2) una forza
(d)
Analogamente, la carica q(2) esercita sulla carica q(1) una forza

dove il raggio vettore è orientato dalla carica 2 verso la carica 1.
Se le velocità v(1) e v(2) sono parallele, equiverse e perpendicolari al vettore , le forze saranno forze di attrazione reciproca se le cariche sono dello stesso segno, e forze di repulsione se sono di segni opposti. Il modulo di queste forze è determinato dalla formula

Nel caso particolare in cui le velocità delle cariche sono uguali risulta

Se le forze sono antiparallele, nelle medesime condizione due cariche dello stesso segno si respingeranno e cariche di segni contrari si attireranno.
Nel caso generale le forze di interazione magnetica non soddisfano al principio di uguaglianza dell’azione e reazione. Le violazioni di questo principio sono particolarmente evidenti quando le velocità v(1) e v(2) sono perpendicolari, e la velocità v(2) è diretta lungo il vettore.

In questo caso e per conseguenza , mentre come si vede nella figura . Ma abbiamo già notato più volte che nel caso di interazioni che avvengono tramite campi, il principio di uguaglianza dell’azione e della reazione non è necessariamente rispettato.

La formula (g) mostra che il rapporto tra la forza di interazione magnetica delle cariche in movimento e la forza della loro attrazione o repulsione coulombiana è dell’ordine di . Le velocità degli elettroni nei metalli percorsi da una corrente elettrica a regime non superano qualche centimetro per secondo e negli elettroliti esse sono ancora più piccole. Il rapporto è quindi molto piccolo e non supera pressappoco . Perché allora i motori elettrici vengono messi in moto proprio dalle forze magnetiche (di Ampère9 rispetto alle quali le forze di interazione elettrostatica non giocano praticamente nessun ruolo? Il fatto è che al trasporto della corrente partecipa un enorme numero di particelle cariche ed è questo che compensa la piccolezza del fattore . E’ importante anche osservare che l’azione del campo magnetico su una carica mobile q dipende non dai valori di q e v presi separatamente, ma dal loro prodotto qv. Quando una corrente circola, le cariche di segni contrari si muovono in direzioni opposte, e quindi il prodotto qv ha lo steso segno per tutti i portatori di corrente. Le forze che si esercitano in un campo magnetico su particelle di differenti segni si sommano aritmeticamente e non si sottraggono. I campi magnetici creati dalle cariche in moto dipendono anch’essi dal prodotto qv, e di conseguenza i campi eccitati da cariche di segni contrari si sommano aritmeticamente. E’ tutt’altro il comportamento delle cariche elettriche rispetto ai campi elettrici. Dato che le forze che si esercitano sulle cariche di segni contrari hanno direzioni opposte, esse si sottraggono aritmeticamente. D’altra parte, anche in un corpo elettricamente carico, le cariche di un dato segno sono in larga misura compensate dalle cariche di segno contrario. Per quanto sia grande la carica elettrica di un corpo, essa è infinitesima rispetto alla carica totale delle particelle dello stesso segno contenute nel corpo. Ecco perché le forze magnetiche superano notevolmente le forze elettriche che si esercitano sulle cariche non compensate dei corpi.
Stabiliamo ora una legge che permette di determinare il campo magnetico di un singolo elemento di corrente. Come abbiamo fatto in elettrostatica, partiremo dal principio di sovrapposizione, che è una generalizzazione dei dati sperimentali. Secondo questo principio, i campi magnetici creati da differenti cariche in movimento si sommano vettorialmente, e il campo eccitato da ciascuna carica non è assolutamente influenzato dall’esistenza delle altre. Il principio di sovrapposizione conduce per il campo magnetico di un elemento volumetrico alla seguente espressione

Analogamente per un elemento lineare di corrente

Queste relazioni esprimono la legge nota come legge di Biot (1774-1862) e Savart (1791-1841). Il campo totale si ottiene integrando le espressioni (h) e (i) su tutte le correnti

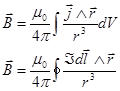
Le due espressioni sono valide solo per le correnti continue. Ma le correnti continue sono sempre delle correnti chiuse. Nessuna delle grandezze osservate subirebbe modifiche se si aggiungesse al secondo membro della formula (i) un termine arbitrario il cui integrale si annulli su un qualunque contorno chiuso. Perciò nel quadro della teoria delle correnti continue la legge elementare di Biot-Savart è in via di principio sperimentalmente incontrollabile, perché è impossibile isolare singoli elementi di correnti continue al fine di sottoporli agli esperimenti. La legge di Biot-Savart espressa in forma integrale è invece sperimentalmente controllabile. Per questa ragione la nostra esposizione della teoria del campo magnetico delle correnti continue si basa sulla legge che determina il campo magnetico di una carica in movimento e non sulla legge elementare di Biot-Savart come è generalmente in uso. In via di principio il campo creato da una carica in movimento può sempre essere misurato, sebbene praticamente ciò sia un esperimento assai arduo. La verifica sperimentale del fatto che le cariche macroscopiche mobili creano campi magnetici richiese sforzi notevoli. Per la prima volta vi riuscì nel 1871 Rowland (1848-1901), che lavorava nel laboratorio di Helmholtz (1821-1894).

Fonte: http://www.liceocopernico.gov.it/oldcop/docenti/matfis/filesharing/downloader.php?id=19&ccr=true

Sito web da visitare: http://www.liceocopernico.gov.it

Autore del testo: indicato nel documento di origine

Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.

Campo magnetico

"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco

www.riassuntini.com dove ritrovare l'informazione quando questa serve