Fisica baricentro

BARICENTRO
Poiché il peso è una forza sempre presente, ogni corpo è soggetto a rotazione a causa del suo momento. Il calcolo del momento del peso però non è immediato poiché se l’oggetto è esteso è evidente che su di un esso non agisce un’unica forza-peso ma piuttosto tantissime piccole forze-peso distribuite su tutto il suo volume.
Per comprendere meglio la cosa, supponiamo di dividere un corpo esteso di massa M in N volumi, rispettivamente di massa m1 , m2,…, mN: il peso di ogni singolo volumetto è p1 = m1×g , p2=m2×g,…, pN=mN×g (vedi figura 1). La forza peso totale P è la somma di tutte queste forze e dunque P=p1 + p2 +…+pN = (m1+m2+…+mN)×g = M×g, come abbiamo sempre supposto. Ma qual è il momento totale che il peso applica sul corpo? E’ evidente che ogni volume ha il suo momento: t1=p1×b1, t2=p2×b2,…, tN=pN×bN. Il momento complessivo t è dato dalla somma dei momenti di tutti gli elementi: t=t1 + t2 +…+tN.
Il calcolo di tale somma è possibile usando la teoria degli integrali: per noi è sufficiente sapere che è dimostrato che
per il calcolo del momento complessivo del peso, si può supporre che tutto il peso sia concentrato in un unico punto B (detto baricentro)
Alternativamente possiamo riformulare la frase dicendo che:
per ogni corpo esiste un unico baricentro dove possiamo immaginare essere concentrato tutto il peso
Una volta noto il baricentro B di un corpo, il momento esercitato dal peso P è immediatamente calcolato come t=P×bP , con bP il braccio di P rispetto a B  
La posizione del baricentro di un corpo dipende dalla forma, estensione e distribuzione della massa all’interno del corpo. Per una figura di forma regolare ed omogenea il baricentro è nel suo centro geometrico; per una figura irregolare o con distribuzione delle masse non omogenea il baricentro tende verso la parte più pesante.
Un semplice modo empirico per determinare il baricentro di un corpo sottile e leggero è quello di… tenere in equilibrio l’oggetto sopra un dito! Se il dito non coincide con il baricentro allora il momento del peso lo farà cadere ruotando; se invece il dito giace proprio sotto al baricentro, il momento del peso di annulla (bP=0) ed il corpo rimane in equilibrio (anche se poi cade alla minima vibrazione). Possiamo perciò affermare che: un corpo sospeso sopra il baricentro rimane in equilibrio. Questa proprietà di per se stessa non ha molta importanza (nessuno si mette a sospendere per aria trattori, camion, macchine agricole in generale alla ricerca del baricentro) ma è utile per ciò che diremo subito dopo.

SPOSTAMENTO DEL BARICENTRO
L’attività di carico/scarico da un mezzo è molto comune: ma aggiungere o togliere una qualche massa da un corpo –ad esempio caricando un carrello o svuotandolo- cambia la posizione del baricentro. Vediamo in che modo.
Supponiamo di avere una qualche massa MA  avente baricentro al punto B; supponiamo di aggiungere una seconda massa MB alla distanza L: il baricentro si sposterà sicuramente dalla parte di MB, finendo in B’. Ci chiediamo qual è il tratto bX  dello spostamento. Per calcolarlo utilizziamo la proprietà appena enunciata, cioè che un corpo tenuto sospeso per il baricentro rimane stabile. Ciò vuol dire che, rispetto a B’, il momento di MA –ruotante anti-orario- è uguale in modulo a quello di MB –ruotante orario- (vedi figura 3). In formule:        
MA×bX = MB×(L-bX) ---> (dopo semplici calcoli) ---> bX = L×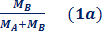
Se MB è trascurabile rispetto a MA allora bX@0 (il baricentro non si sposta da B) ; se MB è molto più grande di MA allora bX»L (il baricentro si sposta su MB). Per tutti gli altri casi, il baricentro si sposta da qualche parte nel segmento unente MA con MB.
L’eq. (1a) è semplificabile se divido la frazione 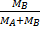  sopra e sotto per MB: se chiamo r=MA/MB (cioè r rappresenta il rapporto fra MA e MB) ottengo subito
bX= L×
L’eq. (1b) sembra un semplice artificio ma permette un rapido calcolo della posizione del nuovo baricentro B’: infatti, supponiamo che MB sia la metà di MA: allora MA/MB = r = 2:1 ---> bX=L/(2+1) = L/3. Se invece MB è un terzo di MA allora MA/MB = r = 3:1 ---> bX=L/(3+1) = 1/4. Se MB è un quinto  di MA: allora MA/MB = r = 5:1 ---> bX=L/(5+1) = 1/6; ecc.