Fisica orologio a luce

L’OROLOGIO A LUCE: la velocità della luce è assoluta!
Il postulato di Einstein secondo cui “La velocità della luce - e quindi di tutte le onde elettromagnetiche -  nel vuoto ha lo stesso valore c in tutti i sistemi inerziali” introduce il concetto di velocità assoluta (quella della luce): questo postulato è assolutamente estraneo alla meccanica Newtoniana  che aveva invece assunto il concetto di accelerazione assoluta, per sistemi di riferimento in moto relativo rettilineo ed uniforme. Ricordiamo che nella teoria classica le velocità dei corpi non sono assolute perché sono definite dalla relazione:

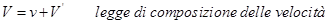
É chiaro che l'introduzione di questo concetto dovrà produrre una radicale revisione delle nostre idee di spazio e di tempo, e ciò lo si può capire se si esamina il cosiddetto orologio a luce.

Un orologio a luce può essere pensato come un dispositivo costituito da una sorgente A che manda un segnale luminoso verso l'alto, dove, a distanza S, c'é uno specchio che riflette la luce verso il basso nel punto B, facendola ritornare in A. Nello stesso posto della sorgente c'é anche un rivelatore che vede il segnale riflesso, lo registra, e invia un nuovo segnale verso B. Ogni volta che il segnale ritorna in A viene emesso un ticchettio che rappresenta l'unità di tempo segnata dal nostro orologio. L'intervallo di tempo "base" dell’orologio a luce sarà, dunque, il tempo impiegato dalla luce per andare da A a B e ritornare in A: lo indicheremo con  Δτ e lo chiameremo tempo proprio dell'orologio. Il tempo Δτ dipende esclusivamente dalla distanza sorgente-specchio e vale.

Immaginiamo ora che l’orologio sia in moto – ad esempio su un treno- rispetto a noi (sistema del laboratorio)con velocità v, "verso destra", e vediamo come ci appariranno le cose.

Dilatazione dei tempi. Indichiamo con Δx la distanza percorsa dall'orologio mentre il segnale luminoso va da A a B e ritorno, con Δt il tempo segnato dall'orologio del nostro laboratorio.

Tenendo conto che la luce viaggia sempre a velocità c, applicando il teorema di Pitagora al triangolo A1B2A2, otterremo:

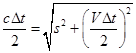
Da quest’ultima relazione si può ricavare Δt e, ricordando il valore trovato per Δτ, si ottiene la formula seguente:

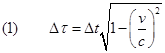
Questa famosa formula è nota come formula per la dilatazione dei tempi negli orologi in moto. Questo nome, forse più di effetto che di sostanza, è legato al fatto che da questa formula si deduce che se noi leggiamo, sul quadrante del nostro orologio nel laboratorio, l'intervallo di tempo che intercorre tra la partenza e il ritorno del segnale luminoso dell'orologio a luce, questo tempo (Δt) sarà più grande di quello (Δτ) segnato sul quadrante dell'orologio a luce: è come se, dal nostro punto di vista l'orologio in moto avesse rallentato. Non c'è nulla di strano o di misterioso in questo, tutto è legato al fatto che l'evidenza sperimentale ci ha costretto ad ammettere che la velocità della luce è uguale sia che la misuriamo dal punto di vista dell'orologio a luce, sia che la misuriamo dal punto di vista del laboratorio, nel quale l'orologio che emette e riceve il raggio di luce è in movimento. É chiaro che questo fatto non è facile da digerire, ma non c'è nulla da fare, visto che tutti gli esperimenti lo confermano con precisione praticamente assoluta. 
Ci si potrebbe chiedere perché nessuno ci ha mai pensato prima di Einstein, o comunque prima della fine del secolo scorso: il motivo è certamente da ricondurre al fatto che, nella pratica della nostra vita quotidiana , anche di sperimentatori nei laboratori scientifici, il fattore di correzione che rende il valore di Δτ diverso da quello di Δt è , cioè un valore estremamente piccolo, per velocità ordinarie.

Contrazione delle lunghezze. Supponiamo ora che il nostro orologio a luce si muova con una velocità v parallela al tratto AB. Con le stesse notazioni di prima, sul quadrante dell'orologio a luce troveremo lo stesso identico risultato: 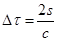. Consideriamo ora la situazione che vede un osservatore nel laboratorio, rispetto al quale l'orologio è in moto verso destra con velocità v.

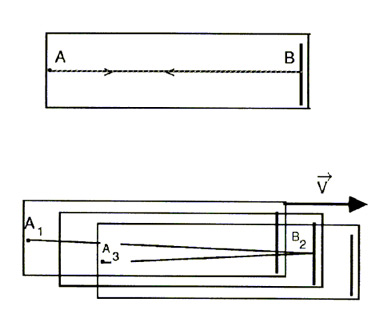
Nella figura qui sopra abbiamo rappresentato, dopo l'immagine dell'orologio a luce nel suo riferimento (del treno), tre successive posizioni dell'orologio a luce viste dal sistema del laboratorio (emissione del segnale, riflessione sullo specchio, ritorno alla sorgente) un po' sfalsate, per rendere più leggibile il disegno. Il lampo emesso dalla sorgente si riflette sullo specchio dopo aver percorso il tratto A1B2 e ritorna alla sorgente dopo aver percorso il tratto B2A3. Indichiamo con l la lunghezza dell'orologio misurata dall'osservatore solidale al laboratorio (che non sappiamo se sarà uguale a S oppure no), con Δt1 il tempo di "andata", con Δt2 quello di "ritorno". Per trovare questi due tempi basterà che teniamo conto che, mentre il segnale viaggia, A e B si spostano, per effetto della velocità v. Si ha, facilmente,. 

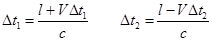
Da qui si possono ricavare i valori dei due intervalli di tempo che, sommati, danno il valore di Δt:

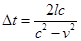
Basterà ora ricordare il già trovato legame tra Δτ e Δt per ricavare la seguente formula:

.
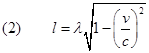
Questa formula è detta formula per la contrazione delle lunghezze di Lorentz-Fitzgerald, perché essa implica che la lunghezza l è più piccola della lunghezza λ. La contrazione delle lunghezze è perfettamente simmetrica alla dilatazione dei tempi e la cosa si può ben vedere nell'esperimento sui muoni.
L’invariante spazio-tempo. Le due formule (1) e (2) hanno avuto una notevole importanza storica e sono, ancora oggi, normalmente presentate come due dei risultati chiave della teoria della relatività. In realtà, senza negare la loro importanza e il fatto che i concetti che esse esprimono sono, forse, due dei concetti più difficili da digerire e per questo più affascinanti soprattutto per i non addetti ai lavori, si potrebbe tranquillamente parlare di relatività senza mai parlare di dilatazione dei tempi e di contrazione delle lunghezze. Molto più importante è il discorso che segue. Riprendiamo in considerazione una formula che ci è servita per ricavare la legge di dilatazione dei tempi:

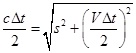
Se scriviamo Δx al posto di VΔt (si tratta dello spostamento subito dall'orologio a luce nel laboratorio) e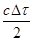
Se considerassimo il moto dello stesso orologio con una diversa velocità, v', troveremmo diversi valori per Δx e Δt (rispettivamente Δx1 e Δt1), ma si avrebbe sempre 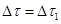, ovvero:

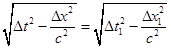
Quadrando, riordinando e riducendo allo stesso denominatore si può ottenere la seguente conclusione fondamentale:

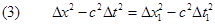
Questa formula esprime il fatto che mentre la lunghezza e il tempo, per proprio conto, dipendono dal riferimento, la combinazione . Questa formula esprime il fatto che la distanza è un invariante, mentre la differenza di ascisse e di ordinate non lo è. Tra questo invariante e quello della relatività ci sono due differenze: la presenza di c2 (ma questa è una questione secondaria dipendente solo dalle unità di misura), e la presenza del segno meno davanti a c2Δt2. Nonostante questo fatto la similitudine tra le due formule è così forte che essa ha dato origine a una trattazione "geometrica" della teoria della relatività (iniziata da Minkowski in un articolo del 1908).