I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Enunciato
Nel vuoto, il flusso del campo elettrico attraverso una qualunque superficie chiusa è uguale alla carica interna fratto la costante dielettrica del vuoto.
In sintesi:
Dimostrazione
Per fare la dimostrazione in modo rigoroso servirebbero alcuni strumenti matematici di cui ancora non disponiamo. Procediamo quindi per via elementare dimostrando il teorema in casi particolari e generalizzando poi il risultato.
1° caso:
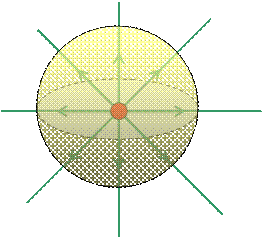
Sorgente di campo elettrico: carica puntiforme Q (per semplicità positiva, ma la dimostrazione è analoga in caso di carica negativa)
Superficie chiusa considerata: una generica sfera di raggio r che ha il centro in Q.
In questo caso sappiamo che il campo è radiale, uscente e di modulo pari a 
.
Osserviamo che su ogni superficie infinitesima la normale e il campo sono paralleli, quindi:
inoltre ogni punto della sfera si trova a distanza fissa r dalla carica sorgente, quindi il modulo del campo è costante (
) e si può portar fuori dall’integrale (o, se pensiamo ad una somma infinita di termini infinitesimi, si può raccogliere), quindi:
, infine 
Si ottiene così la tesi 
2° caso
Sorgente di campo elettrico: carica puntiforme Q (per esempio positiva, ma la dimostrazione è analoga in caso di carica negativa)
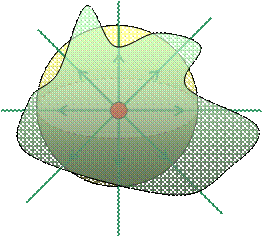
Superficie chiusa considerata: una generica superficie contenente Q. (superficie verde)
Ricordiamo che dal punto di vista qualitativo il flusso rappresenta il numero di linee di campo che attraversano una superficie, in particolare, se due superfici sono attraversate dalle stesse linee di campo, i flussi attraverso di esse saranno uguali.
Guardando il disegno, notiamo che le linee di campo che attraversano la sfera (gialla) sono tutte e sole quelle che attraversano la generica superficie chiusa (verde), per quanto ricordato sopra:
, ma data la dimostrazione fatta nel 1° caso si avrà che
, cioè la tesi.
3° caso
Sorgente di campo elettrico: carica puntiforme Q (per esempio positiva, ma la dimostrazione è analoga in caso di carica negativa)
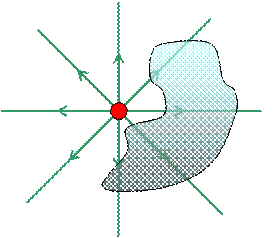
Superficie chiusa considerata: una generica superficie NON contenente Q. (superficie azzurra)
Ricordiamo che dal punto di vista qualitativo il flusso rappresenta il numero di linee di campo che attraversano una superficie, in particolare, data una superficie chiusa, se il numero di linee entranti è uguale a quello di quelle uscenti, il flusso è nullo.
Guardando il disegno si osserva che ciascuna linea entra ed esce dalla superficie azzurra, dando così un contributo nullo. Quindi, se la carica non è contenuta nella superficie, in accordo con quanto vogliamo dimostrare 
4° caso
Sorgente di campo elettrico: una generica distribuzione di carica (N cariche puntiformi)
Superficie chiusa considerata: una generica superficie.
Per considerare il caso generale, ricordiamo il principio di sovrapposizione degli effetti, cioè il campo elettrico generato da più sorgenti è la somma vettoriale dei campi che ciascuna sorgente genererebbe se fosse da sola: 
, essendo il flusso un operatore lineare (cioè il flusso di una somma è uguale alla somma dei flussi), si potrà scrivere:
Per le dimostrazioni fatte nei casi precedenti, i termini di questa somma sono nulli se la carica non è contenuta nella superficie chiusa, oppure pari al valore della carica fratto la costante dielettrica del vuoto se la carica è contenuta nella superficie chiusa); in pratica ciò che rimane è 
, cioè la tesi.
Nell’esempio rappresentato avremmo:
Fonte: http://www.liceomeda.it/new/documenti/0809/Materiali/Teorema%20di%20Gauss.doc
Sito web da visitare: http://www.liceomeda.it
Autore del testo: indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve