Cinematismo della biella

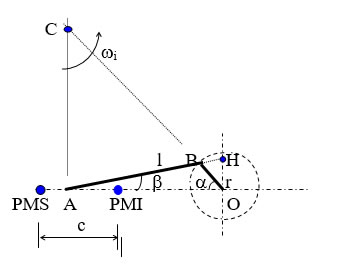
Nella figura è riprodotto lo schema del meccanismo biella – manovella che consente di convertire un moto circolare in un moto rettilineo alternato e viceversa. Il tratto OB rappresenta la manovella di lunghezza r. Il tratto AB rappresenta la biella di lunghezza l. Il punto A è detto piede di biella ed ha un moto rettilineo alternato che va dal PMS punto morto superiore al PMI punto morto inferiore. La distanza di questi due punti è detta corsa c. Il punto B è detto testa di biella ed ha un moto circolare di centro O, normalmente uniforme con velocità angolare w. Poiché i suoi punti estremi hanno moti diversi, la biella come corpo rigido avrà un movimento complesso che tiene conto del moto rettilineo alternato del piede e del moto circolare uniforme della testa. In una generica posizione, quale quella mostrata in figura, la manovella e la biella formano rispettivamente gli angoli a e b con la direzione del moto del piede. Il nostro intento è trovare le relazioni che legano la posizione, la velocità e l’accelerazione del piede di biella, agli angoli a e b e alle lunghezze l ed r.
Il movimento infinitesimo della biella come corpo rigido si può pensare come una rotazione intorno a C centro istantaneo di rotazione, alla velocità istantanea wi . I punti A e B quindi percorrono una traettoria circolare di centro C con velocità periferiche   vA = AC wi  ;  vB = BC wi . Possiamo scrivere dividendo membro a membro   vA : vB = AC : BC
L’intersezione del prolungamento del segmento AB con l’ortogonale alla retta AO  uscente da O è il punto H segnato in figura. I triangoli ABC ed OBH sono simili per cui  AC : BC = OH : OB   Da notare che OB = r.
Le due relazioni soprascritte si condensano in  vA : vB = OH : r
La testa di biella B ha velocità periferica costante  vB = w r

Adesso, come si vede dalla figura, portando da O l’ortogonale a BH  si trova il punto N e risulta          ON = OH cos b        
ma anche                                ON = r sen(a+b)
da cui      OH cos b = r sen(a+b)  cioè      OH = r sen(a+b)/cos b
per cui trovo che la velocità del piede di biella in funzione degli angoli a e b e della velocità angolare w risulta:
vA = vB OH/r = w r sen(a+b)/cos b
Applicando il teorema dei seni al triangolo AOB possiamo scrivere:
r : sen b = l : sen a      oppure       r : l = sen b : sen a
chiamando   l = r/l    il rapporto tra le lunghezze di manovella e biella ottengo che      sen b = l sen a
da cui      cos b = √(1 – sen² b) = √(1 – l² sen² a)  ≅ 1   stante la piccolezza del termine     l² sen² a.
Ben conosciute formule trigonometriche ci dicono che:
sen (a+b) = sen a cos b + cos a sen b = sen a + cos a l sen a =
= sen a + l sen a cos a = sen a + (l sen 2a) / 2
Potremo infine scrivere la velocità del piede di biella:
vA = w r [sen a + (l sen 2a) / 2]
Avendo unità di misura  w [rad/s],  r [m],  a [rad]  otteniamo vA [m/s]
Questa espressione ci dà la velocità del piede di biella in funzione dell’angolo di manovella a, essendo tutti gli altri parametri costanti.
Possiamo disegnare il grafico di vA in funzione di a o in funzione del tempo t (risulta simile poiché a aumenta uniformemente con t). Nell’Ariosi il grafico è in figura 1.9. Il grafico è approssimativamente sinusoidale. La velocità massima si ha per un angolo a leggermente inferiore a 90°, precisamente nella posizione di quadratura, ossia quando biella e manovella hanno direzioni ortogonali.
A volte è utile considerare la velocità media del piede di biella vAm calcolata come il rapporto tra lo spazio percorso e il tempo impiegato durante un giro di manovella. Lo spazio percorso è due volte la corsa c [m], il tempo impiegato è il periodo  T = 60/n  [s]   in cui   n [giri/min]   è la frequenza di rotazione della manovella.
E’ quindi    vAm = 2c/T = cn/30  [m/s]

Derivando l’espressione della velocità rispetto al tempo, troviamo anche l’accelerazione del piede di biella:
aA = dvA/dt = dvA/da • da/dt = w dvA/da = w w r [cos a + l 2 cos(2a) /2]
aA = w² r [cos a + l cos(2a)]
Avendo unità di misura  w [rad/s],  r [m],  a [rad]  otteniamo aA [m/s²]
E’ importante notare che aA risulta la somma di due termini:
accelerazione del primo ordine aI = w² r cos a 
accelerazione del secondo ordine   aII = w² r l cos(2a)
Nell’Ariosi troviamo il grafico di aA in funzione di a (o di t) nella figura 1.10. Anche questo grafico è di tipo sinusoidale. Notiamo che l’accelerazione massima (positiva e negativa) si ha per a = 0° e a = 180°, cioè quando la biella inverte la direzione del moto. L’accelerazione è invece nulla in posizione di quadratura, quando è massima la velocità vA.
E’ interessante anche il grafico che riporta la variazione di aA in funzione della posizione s del piede di biella (nell’Ariosi figura 1.11), poiché si notano due cose: l’accelerazione del piede di biella si annulla un po’ prima di metà corsa, e il suo massimo positivo è maggiore in valore assoluto del suo massimo negativo. Queste considerazioni sono molto importanti per la dinamica della biella.