I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Teorema di Boucherot
In un sistema elettrico in regime sinusoidale costituito da più utilizzatori si può dire che:
a) la potenza attiva totale è data dalla somma aritmetica delle singole potenze attive:
b) la potenza reattiva totale è data dalla somma algebrica delle singole potenze reattive assunte positive se induttive, negative se capacitive:
c) la potenza apparente complessa totale è data dalla somma vettoriale delle singole potenze apparenti complesse, in ogni caso il modulo della potenza apparente totale si può più convenientemente determinare con:
Esercizio N° 11 (risoluzione circuito in c.a., applicazione di Boucherot)
Si abbia la seguente rete in corrente alternata:
1) Determinare le correnti nei tre rami.
Per prima cosa si passa al circuito alle impedenze determinando per ciascun ramo la corrispondente impedenza ed esprimendo la f.e.m. nota in forma simbolica:
[W]
[W]
[W]
Quindi si applicano al circuito alle impedenze le solite regole di risoluzione delle reti. Nel caso in esame vi è un solo generatore e risulta possibile risolvere la rete attraverso la riduzione successiva delle impedenze. Le impedenze 
e 
sono in parallelo:
[W]
La rete diventa quindi:
Applicando a questa rete la legge generale di Ohm si può calcolare la corrente 
:
Si osserva che tale corrente è in ritardo rispetto alla f.e.m. del generatore, quindi l’impedenza totale vista ai morsetti del generatore sarà di natura ohmico−induttiva.
Per determinare le correnti nelle due impedenze in parallelo determino prima la tensione ai capi del parallelo:
Quindi dividendo tale tensione per ciascuna delle impedenze trovo le correnti:
A titolo di controllo si può applicare il primo principio di Kirchhoff al nodo A e attestare così che esso è verificato.
Il diagramma vettoriale rappresentativo delle tensioni e correnti alternate calcolate è il seguente:
Le espressioni ai valori istantanei delle tre correnti sono le seguenti:
A tali espressioni corrispondono gli oscillogrammi:
2) Determinare la potenza erogata dal generatore ideale di tensione.
Trattandosi di un generatore di corrente alternata avremo erogazione sia di potenza attiva che reattiva. Entrambe le potenze dipendono dallo sfasamento tra la f.e.m. e la corrente erogata:
Le potenze attiva e reattiva erogate valgono quindi:
Si osserva che lo sfasamento tra la f.e.m. del generatore e la corrente da esso erogata corrisponde all’argomento della impedenza totale 
vista ai morsetti del generatore stesso:
[W]
Si conferma inoltre la natura ohmico−induttiva dell’impedenza totale.
3) Determinare le potenze attiva e reattiva complessivamente impegnate dalle impedenze.
Queste potenze si possono calcolare applicando il teorema di Boucherot:
[W]
[VAR] induttivi
Le potenze totali potevano ovviamente essere pure determinate utilizzando l’impedenza totale:
[W]
[VAR] induttivi
Ovviamente le potenze erogate dal generatore corrispondono alle potenze impegnate dalle impedenze.
Linee semplici monofase, rifasamento
Sono quelle per le quali è valido il seguente circuito equivalente:
Si definisce caduta di tensione industriale della linea la differenza aritmetica tra la tensione all'arrivo a vuoto e la tensione all'arrivo a carico:
calcolabile con l'espressione semplificata:
Si definisce rendimento della linea:
dove PA = PU è la potenza all'arrivo della linea mentre PP è la potenza alla partenza della linea.
Al fine di ridurre la c.d.t. industriale ed aumentare il rendimento della linea, se il carico ha un basso fattore di potenza si può procedere al rifasamento del carico stesso che consiste nel porgli in parallelo un condensatore di adeguata capacità. Indicando con jA* lo sfasamento desiderato all'arrivo della linea (con ovviamente jA* < jU ), il valore della capacità rifasante sarà dato da:
Esercizio N° 12 (circuito in c.a., linea monofase con nota la tensione all’arrivo)
Una linea elettrica in corrente alternata monofase alimenta alla tensione VA=230 [V], f=50 [Hz] i seguenti carichi:
1) un’impedenza formata dalla serie di una resistenza R=8 [W] e di una induttanza L=19,1 [mH];
2) un carico ohmico-capacitivo che assorbe la potenza PU2=2 [kW] con fattore di potenza cosjU2=0,85 in anticipo;
3) un motore a induzione di rendimento h=0,85 e fattore di potenza cosjU3=0,8 in ritardo il cui albero ruota alla velocità n=1400 [rpm] ed eroga la coppia C=10 [N·m].
Sapendo che la linea ha resistenza RL=0,2 [W] e reattanza XL=0,15 [W], determinare:
1) la corrente nella linea ed il fattore di potenza all’arrivo della linea;
2) la tensione ed il fattore di potenza alla partenza della linea;
3) la caduta di tensione industriale ed il rendimento della linea;
4) la capacità per il rifasamento totale all’arrivo della linea e la nuova corrente di linea nell’ipotesi che la tensione all’arrivo rimanga costante.
Risposta alla domanda 1)
Per prima cosa si trova il carico complessivo equivalente ai tre carichi applicati alla linea. Per fare questo si applica il teorema di Boucherot ed inizio calcolando le potenze attiva e reattiva assorbite dai singoli carichi.
Primo carico:
Secondo carico:
Nel secondo carico, essendo il fattore di potenza in anticipo, la potenza reattiva impegnata è di natura capacitiva.
Terzo carico:
Come si nota ho prima calcolato la potenza meccanica erogata dal motore e successivamente la potenza elettrica assorbita dividendo per il rendimento.
Applico ora il teorema di Boucherot:
Posso ora calcolare la corrente di linea ed il fattore di potenza all’arrivo:
Risposta alla domanda 2)
Applicando ancora Boucherot risalgo nella sezione di monte della linea:
Posso ora calcolare la tensione ed il fattore di potenza alla partenza:
Risposta alla domanda 3)
Sapendo che la caduta di tensione industriale è la differenza aritmetica tra la tensione all’arrivo a vuoto e la tensione all’arrivo a carico ho:
Si può anche usare l’espressione approssimata:
Il rendimento sarà dato da:
Risposta alla domanda 4)
Il rifasamento totale presuppone che la capacità rifasante impegni una potenza reattiva pari all’intera potenza reattiva induttiva in modo tale che il fattore di potenza dopo il rifasamento sia unitario:
La corrente di linea dopo il rifasamento si può determinare tenendo conto del fatto che in conseguenza del rifasamento cambia il fattore di potenza ma non la potenza attiva (l’inserzione del condensatore di rifasamento influisce sulla potenza reattiva):
Si osserva che si ha una riduzione della corrente di linea che comporta una minore caduta di tensione industriale ed un maggior rendimento della linea.
Esercizio N° 13 (circuito in c.a., linea monofase con nota la tensione alla partenza)
Una linea elettrica in corrente alternata monofase è alimentata alla tensione VP=230 [V], f=50 [Hz] ed alimenta un carico ohmico-induttivo che assorbe la potenza PA=10 [kW] con fattore di potenza cosjA=0,8 in ritardo.
Sapendo che la linea ha resistenza RL=0,2 [W] e reattanza XL=0,1 [W], determinare:
1) la corrente nella linea e la tensione all’arrivo;
2) il fattore di potenza alla partenza della linea;
3) la caduta di tensione industriale ed il rendimento della linea;
4) la capacità per il rifasamento a 0,92 in ritardo della partenza della linea.
Risposta alla domanda 1)
In questo caso non è possibile il calcolo diretto della corrente di linea in quanto si conosce la tensione alla partenza e la potenza all’arrivo e le due grandezze non possono essere poste direttamente in relazione. Si può tuttavia scrivere un sistema di secondo grado usando l’espressione della potenza all’arrivo e l’espressione approssimata della caduta di tensione industriale la cui risoluzione fornisce il valore della corrente di linea e della tensione all’arrivo:
Delle due soluzioni ottenute solo la seconda è accettabile in quanto compatibile con le caratteristiche della linea. Infatti è impensabile che una linea con alla partenza 230 [V] possa avere all’arrivo solo 12,65 [V], normalmente la caduta di tensione industriale in una linea è contenuta ben al di sotto del 10%. Di conseguenza la soluzione accettabile per il sistema di secondo grado è:
Risposta alla domanda 2)
Applicando Boucherot risalgo nella sezione di monte della linea:
Posso ora calcolare il fattore di potenza alla partenza:
Risposta alla domanda 3)
Sapendo che la caduta di tensione industriale è la differenza aritmetica tra la tensione all’arrivo a vuoto e la tensione all’arrivo a carico ho:
Si osserva che, a meno delle approssimazioni introdotte dai calcoli, la c.d.t. industriale coincide con la soluzione del sistema scartata. Questo è sempre vero e dipende dalla natura algebrica del sistema stesso.
Il rendimento sarà dato da:
Risposta alla domanda 4)
La capacità per il rifasamento a cosjP’=0,92 in ritardo della partenza della linea vale:
Risonanza
Un circuito in corrente alternata, comunque complesso, nel quale siano presenti resistenze, induttanze e capacità si dice in risonanza quando rispetto alla tensione che lo alimenta si comporta come un circuito puramente ohmico.
Si parla di risonanza serie (chiamata anche risonanza di tensione) quando i bipoli R , L , C sono collegati in serie tra di loro. Affinché il circuito si comporti come se fosse puramente ohmico deve ovviamente essere XL = XC . La pulsazione per la quale questa condizione si verifica è chiamata pulsazione di risonanza e vale:
come è facile dimostrare.
Per pulsazioni più grandi di w0 il circuito si comporta da ohmico-induttivo, tendente al puramente induttivo per w0 tendente ad infinito. Per pulsazioni più piccole di w0 il circuito si comporta da ohmico-capacitivo, tendente al puramente capacitivo per w0 tendente a zero.
Se si immagina di alimentare il circuito con un generatore di tensione di valore efficace costante e pulsazione variabile, è facile verificare che in coincidenza della pulsazione di risonanza è massima la corrente che varrà 
[A]. Quindi ai capi dell'induttanza e della capacità si può avere una c.d.t. molto grande, anche maggiore della tensione applicata al circuito. Infatti se per 
si ha XL0 = XC0 >> R accadrà che sarà VL0 = VC0 >> VR0 = V.
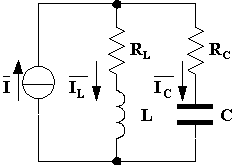
Si parla di risonanza parallelo (chiamata anche risonanza di corrente o antirisonanza) quando si presenta il circuito riportato sopra. La pulsazione di risonanza, per la quale la tensione ai capi del parallelo è in fase con la corrente che lo alimenta, si dimostra che vale:
e, nel caso di RL = RC, tale espressione diventa uguale a quella della risonanza serie. In coincidenza di w0 si ha che il parallelo assume il valore massimo di impedenza (tale impedenza è puramente ohmica) pari a:
Per pulsazioni più grandi di w0 il circuito si comporta da ohmico-capacitivo, tendente al puramente capacitivo per w0 tendente ad infinito. Per pulsazioni più piccole di w0 il circuito si comporta da ohmico-induttivo, tendente al puramente induttivo per w0 tendente a zero.
Se si immagina di alimentare il circuito con un generatore di corrente di valore efficace costante e pulsazione variabile, accade che in coincidenza della pulsazione di risonanza è massima la tensione ai capi del parallelo. Quindi nei rami del parallelo si può avere una corrente molto grande, anche maggiore della corrente erogata dal generatore.
Fonte: http://www.istitutoprimolevi.gov.it/elettrobox/Appunti_Reti%20elettriche%20in%20corrente%20continua%20e%20corrente%20alternata.docx
Sito web da visitare: http://www.istitutoprimolevi.gov.it
Autore del testo: non indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve