I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
2 – Sforzi elettrodinamici
Come prima cosa è opportuno ricordare che fra due conduttori adiacenti percorsi dalla stessa corrente I si generano delle forze meccaniche F il cui valore è dato da ![]() , dove B è il vettore induzione del campo magnetico creato dalla corrente I ed l è il vettore che definisce la lunghezza del conduttore stesso (orientato nel senso di percorrenza della corrente).
, dove B è il vettore induzione del campo magnetico creato dalla corrente I ed l è il vettore che definisce la lunghezza del conduttore stesso (orientato nel senso di percorrenza della corrente).
La direzione secondo cui agiscono le forze F può essere determinata in modo semplice ricorrendo, ad esempio, alla regola di Flaming della mano sinistra, qui di seguito riportata:
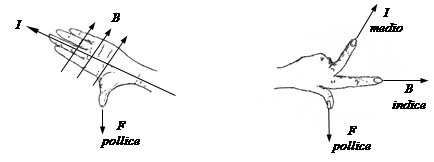
Applicando dunque tale regola a due conduttori paralleli percorsi dalla stessa corrente I, si ricava la situazione qui sotto schematizzata, per cui si ha:

corrente I nella stessa direzione --> forza F di attrazione
corrente I in direzioni opposte --> forza F di repulsione
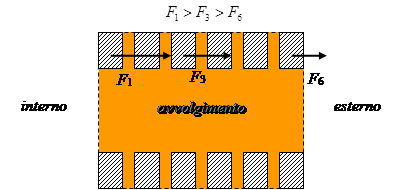
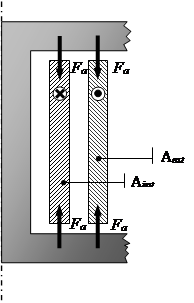
In una sezione di un avvolgimento di trasformatore (formata da quattro conduttori come schematicamente indicato nel disegno), si ha quindi

Applichiamo ora queste semplici osservazioni all’avvolgimento di un trasformatore monofase, prendendo in considerazione un caso semplice costituito da due avvolgimenti cilindrici e coassiali di cui quello esterno (ES) è generalmente di AT, mentre quello interno (INT) è generalmente di BT.
Sulla base delle osservazioni fatte possiamo concludere che fra gli avvolgimenti ES e INT del trasformatore sono sollecitati dalle forze schematicamente indicate nel disegno accanto:
Queste forze dipendono dalla corrente I che percorre gli avvolgimenti e quindi possono raggiungere una notevole intensità in relazione alle sovracorrenti che si verificano a seguito di un corto circuito. Nel progetto di un avvolgimento è dunque necessario determinare le forze meccaniche che sollecitano gli avvolgimenti al fine di prevedere opportuni ancoraggi meccanici che impediscano la deformazione o la distruzione meccanica degli avvolgimenti stessi.
2.1 – Sforzi radiali
Consideriamo dunque un avvolgimento di trasformatore formato da due singoli avvolgimenti, uno esterno (ES) e uno interno (INT), cilindrici e coassiali, separati da un canale, come riportato nello schizzo a lato in cui sono indicate le relative dimensioni.
Nel disegno è anche indicata la distanza elettromagnetica degli avvolgimenti c, data da
![]()
e definita nel par. 4.2 degli appunti “Reattanze degli avvolgimenti”, par. cui faremo esplicito riferimento nello sviluppo dei calcoli che seguono.

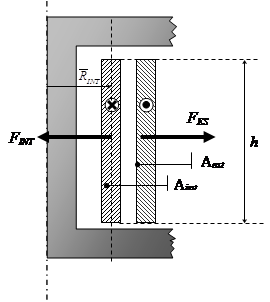
Nel disegno seguente è riportata una sezione di tale avvolgimento in cui vengono evidenziate le forze che sollecitano i due avvolgimenti, di dilatazione per l’avvolgimento esterno e di compressione per l’avvolgimento interno.

Un modo semplice di determinare le forze che sollecitano l’avvolgimento è quello basato sul principio dei lavori virtuali. Indichiamo con W(xyz) l’energia del campo magnetico connesso con gli avvolgimenti e con F(xyz) la forza generata da questo campo magnetico.
Consideriamo una componente di tale forza lungo una determinata coordinata, ad esempio la componente Fx(x ) lungo l’asse x; se la geometria del sistema varia lungo la coordinata x di una quantità infinitesima dx, il lavoro svolta dalla relativa componente della forza F è dato da ![]() . Questo lavoro può svolgersi solo per effetto di una variazione dW dell’energia del campo W, per cui si ha (conservazione dell’energia)
. Questo lavoro può svolgersi solo per effetto di una variazione dW dell’energia del campo W, per cui si ha (conservazione dell’energia) ![]() e quindi
e quindi ![]() .
.
Poiché dobbiamo determinare le forze radiali e supponiamo che entrambi gli avvolgimenti siano costruiti in modo da avere una simmetria cilindrica, assumeremo come coordinata di riferimento la coordinata radiale r .
2.2.1 – Avvolgimento esterno
Per comodità di calcolo, come risulterà evidente nel seguito, assumiamo come coordinata di riferimento la distanza elettromagnetica c (dis. a).
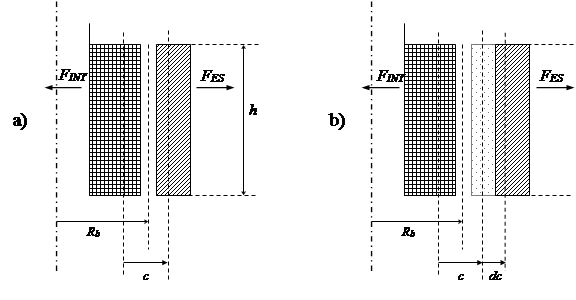
Supponiamo ora che per effetto delle forze FES l’avvolgimento esterno si deformi simmetricamente provocando un incremento dc della coordinata c (dis. b).
Possiamo scrivere ![]() , dove W è l’energia del campo relativa all’intero avvolgimento; quest’ultima è data da
, dove W è l’energia del campo relativa all’intero avvolgimento; quest’ultima è data da ![]() , dove Xcc è la reattanza di corto circuito dell’avvolgimento ed i(t) la corrente che lo percorre (IAT o IBT : vedi “Reattanza degli avvolgimenti”, par. 4.2). Facendo sempre riferimento al par. citato, si ha che la reattanza di cto.cto. è data da
, dove Xcc è la reattanza di corto circuito dell’avvolgimento ed i(t) la corrente che lo percorre (IAT o IBT : vedi “Reattanza degli avvolgimenti”, par. 4.2). Facendo sempre riferimento al par. citato, si ha che la reattanza di cto.cto. è data da
1.1 ![]()
dove N è il numero di spire di un avvolgimento (NAT o NBT) e ![]() è il perimetro medio del canale. Poiché riteniamo che la deformazione dell’avvolgimento sia solo radiale, l’altezza dell’avvolgimento h rimane costante; la 1.1 può dunque essere scritta come
è il perimetro medio del canale. Poiché riteniamo che la deformazione dell’avvolgimento sia solo radiale, l’altezza dell’avvolgimento h rimane costante; la 1.1 può dunque essere scritta come
![]() con
con ![]()
e si ha ![]() , da cui risulta
, da cui risulta
![]()
Per un calcolo di prima approssimazione il valore della costante A può essere determinato dalla reattanza nominale di cto.cto. (valore determinato in assenza di deformazioni dovute al corto circuito), ottenendo ![]() , per cui si ha
, per cui si ha ![]() , cui corrisponde, in relazione al valore di picco Ip della corrente che vale (vedi 3.1)
, cui corrisponde, in relazione al valore di picco Ip della corrente che vale (vedi 3.1) ![]() , un valore massimo
, un valore massimo
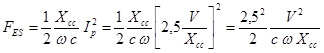
Poiché è ![]() , risulta
, risulta ![]()
1.2 ![]()
Di solito possiamo porre ![]() , per cui la 1.2 diviene
, per cui la 1.2 diviene
1.3 ![]()


dove ![]() è il raggio medio dell’avvolgimento (il fatto di fare riferimento al raggio medio è una semplificazione valida per un calcolo di prima approssimazione).
è il raggio medio dell’avvolgimento (il fatto di fare riferimento al raggio medio è una semplificazione valida per un calcolo di prima approssimazione).
Per valutare lo sforzo che sollecita l’avvolgimento, consideriamo una generica sezione dell’avvolgimento, come indicato nel disegno seguente:
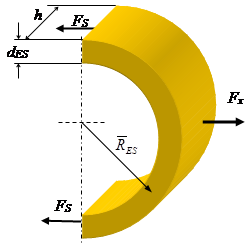

Se indichiamo con ![]() un elemento di superficie del cilindro che costituisce l’avvolgimento, valutato in corrispondenza del raggio medio, la forza dF che agisce su dS è data da
un elemento di superficie del cilindro che costituisce l’avvolgimento, valutato in corrispondenza del raggio medio, la forza dF che agisce su dS è data da
![]()
e la sua componente lungo l’asse x indicato nel disegno è
![]()
La risultante, lungo l’asse x, delle forze che agiscono sul semicilindro che stiamo considerando è quindi

1.5 ![]()
Dalla 1.3 si ha ![]() , per cui si ottiene
, per cui si ottiene
1.6 ![]()
Questa forza è bilanciata dalle due forze di trazione ![]() che agiscono sull’avvolgimento nella sezione considerata; questa sezione di avvolgimento è data da
che agiscono sull’avvolgimento nella sezione considerata; questa sezione di avvolgimento è data da ![]() (le varie grandezze sono specificate nel disegno precedente), per cui è sollecitata da uno sforzo di trazione
(le varie grandezze sono specificate nel disegno precedente), per cui è sollecitata da uno sforzo di trazione
![]()
1.7 ![]()
La 1.7 esprime lo sforzo di trazione che sollecita l’avvolgimento, e tale sforzo deve essere inferiore allo sforzo massimo ammesso smax per quel tipo di struttura: ![]() .
.
A titolo indicativo si può ritenere che per un avvolgimento di trasformatore sia ![]() .
.
Si deve comunque tener presente che lo sforzo definito dalla 1.t è un valore medio, adatto solo ad un calcolo di prima approssimazione, dedotto ritenendo l’avvolgimento come un unico cilindro massiccio ed omogeneo uniformemente sollecitato. In realtà le singole spire che giacciono sullo stesso piano diametrale, anche se percorse dalla stessa densità di corrente, sono sollecitate forze diverse che diminuiscono all’aumentare della distanza dal nucleo (in base alla 1.6 la Fx diminuisce all’aumentare di c): le spire più interne sono sollecitate da una forza maggiore, e quelle più esterna da una forza minore.
La 1.7 può anche essere scritta
![]()
dove ![]() è un fattore che dipende dalla frequenza (50 Hz) e dai parametri geometrici di dimensionamento degli avvolgimenti. Poiché è
è un fattore che dipende dalla frequenza (50 Hz) e dai parametri geometrici di dimensionamento degli avvolgimenti. Poiché è ![]() , si ha anche, facendo riferimento alla tensione nominale (V = Vn) ,
, si ha anche, facendo riferimento alla tensione nominale (V = Vn) ,
![]()
Da quest’ultima relazione possiamo concludere che, a parità di valori di K e della tensione di corto circuito vcc% , lo sforzo aumenta con la potenza nominale della macchina; in realtà anche la tensione di corto circuito aumenta con la potenza nominale, per cui l’incremento degli sforzi meccanici con la potenza nominale ha all’incirca l’andamento mostrato nella figura seguente (valori indicativi):

 2.2.2 – Avvolgimento interno
2.2.2 – Avvolgimento interno
La forza radiale risultante, di compressione, che sollecita l’avvolgimento interno ha (ripetendo lo stesso ragionamento fatto in precedenza) la stessa espressione della 1.3, facendo ovviamente riferimento ai parametri geometrici dell’avvolgimento interno; si ha cioè
2.1 ![]()

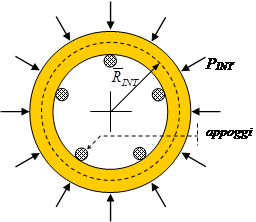
Consideriamo un settore di questo avvolgimento, compreso fra due appoggi contigui come schematizzato nel disegno seguente:

Questo tratto di avvolgimento può essere trattato come una trave, di lunghezza b, spessore dINT e larghezza h, incastrata alle estremità, uniformemente caricata dalla forza ![]() .
.
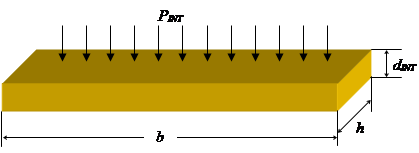
Il modulo di resistenza a flessione di questa trave è dato da ![]() . Sappiamo inoltre che l’andamento del momento flettente che sollecita l’avvolgimento è dato da
. Sappiamo inoltre che l’andamento del momento flettente che sollecita l’avvolgimento è dato da
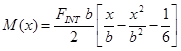
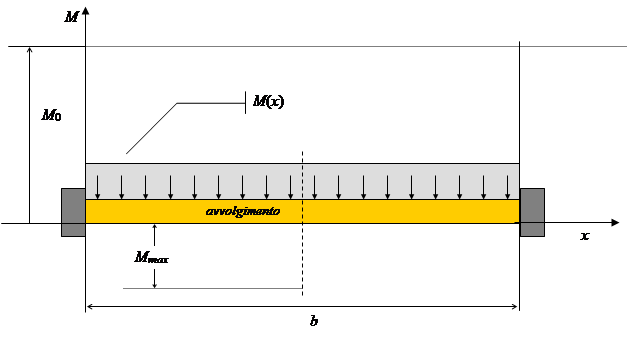
Il momento flettente massimo si ha nella mezzeria della trave e vale
![]()
mentre il momento agli incastri (x = 0 ; x = b) è dato da
![]()
e quest’ultima sollecitazione risulta quella massima (M0 > Mmax) .
Quindi il massimo sforzo a flessione che sollecita l’avvolgimento, che si ha agli incastri, risulta
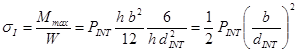
e naturalmente aumenta con la distanza fra gli appoggi b e diminuisce all’aumentare dello spessore dINT dell’avvolgimento. La pressione che sollecita l’avvolgimento interno è data da (rel. 2.2) ![]() , mentre FINT è data dalla 2.1:
, mentre FINT è data dalla 2.1: ![]() . Quindi si ha
. Quindi si ha
![]() ;
; ![]()
con ![]() , e si ottiene ancora
, e si ottiene ancora
![]()
A parità di KINT e della tensione di corto circuito percentuale, lo sforzo a flessione che sollecita l’avvolgimento interno aumenta con la potenza nominale della macchina, con un andamento simile a quello visto per l’avvolgimento esterno.
2.2 – Sforzi assiali
Facciamo sempre riferimento al caso semplice di due avvolgimenti cilindrici e concentrici che possano essere considerati come due elementi omogenei e a perfetta simmetria cilindrica.
Come abbiamo visto le forze generate dalle correnti che circolano negli avvolgimenti sono di compressione per ambedue gli avvolgimenti, e queste forze possono raggiungere valori elevati, e quindi pericolosi per l’integrità meccanica degli avvolgimenti, durante il transitorio di corto circuito.
E’ quindi necessario, per una corretta progettazione, valutare queste forze e gli sforzi di compressione che ne derivano, e per farlo possiamo ricorrere ancora al principio dei lavori virtuali.
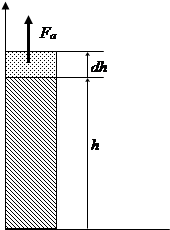
Facciamo dunque riferimento ad un solo avvolgimento (interno o esterno), come schematizzato nel disegno seguente:

Supponiamo inoltre, per semplicità, che la deformazione dovuta alle forzi assiali si manifesti solamente con una variazione dh dell’altezza h dell’avvolgimento; sotto questa ipotesi, e facendo riferimento al sistema di coordinate indicato nel disegno, possiamo scrivere
![]()
dove W è l’energia del campo relativa all’intero avvolgimento data da
![]()
con Xcc reattanza di corto circuito dell’avvolgimento ed i(t) corrente che lo percorre (IAT o IBT : vedi “Reattanza degli avvolgimenti”, par. 4.2). In base a quanto detto nel par. 4.2 citato, la reattanza di cto.cto. è data da
![]()
dove N è il numero di spire di un avvolgimento (NAT o NBT) e p è il perimetro medio del canale (vedi par. 2.2.1); si ha quindi
![]()
e pertanto si ottiene
![]()
La forza FA risulta negativa rispetto al sistema di coordinate utilizzato, e quindi è di compressione. Ilil suo valore massimo si ha in corrispondenza del picco di corrente che vale (vedi 3.1)
![]()
Pertanto il valore della forza assiale di compressione che deve essere utilizzato per il calcolo degli sforzi è dato da
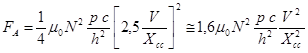
A questa forza corrisponde uno sforzo di compressione dell’avvolgimento
![]()
![]()
dove ![]() è il volume dell’avvolgimento considerato.
è il volume dell’avvolgimento considerato.
Fonte: http://www-3.unipv.it/energy/costruzioni_elettromeccaniche_file/Lezioni%200405/Teoria/Lez7_ctocto%20trafo%20-%20sforzi.doc
Sito web da visitare: http://www-3.unipv.it/
Autore del testo: non indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve