I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
CORSO DI FONDAMENTI DI DISEGNO TECNICO
LEZIONE PROIEZIONI ORTOGONALI
GASPARD MONGE
(1746 - 1818)
alla Scuola del Genio di Mezieres codifica una nuova disciplina
alla quale dà il nome di
GEOMETRIA DESCRITTIVA

in realtà, il metodo della doppia proiezione ortogonale, in pianta ed in alzato, era già noto sin dall’antichità, da Vitruvio (I secolo a.C.)
a Piero della Francesca (1412 ? – 1492):
De Prospectiva Pingendi
e fu ripreso da molti altri studiosi, tanto che Lagrange commentò: “Je ne savais pas que je savais la Géométrie Descriptive”
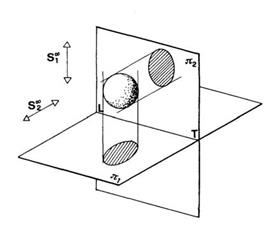
l’innovazione di Monge è stata quella di rappresentare gli elementi fondamentali (punto, retta, piano)
in relazione ad un ben preciso sistema di riferimento:
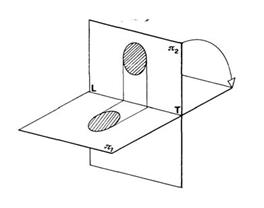
con un’operazione di ribaltamento, i due piani vengono portati a coincidere con il foglio da disegno
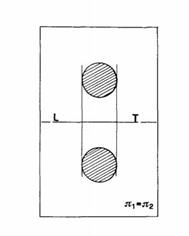
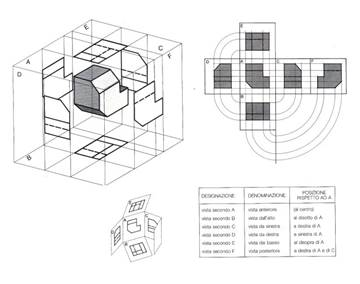
si ottengono così, sul foglio, più rappresentazioni dello stesso oggetto:
sono più immagini sovrapposte
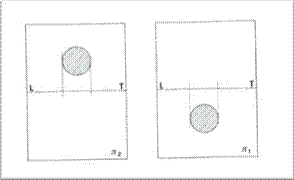
PIANTA

per ricostruire il solido, occorre coordinare le informazioni date dalle diverse proiezioni
lette insieme, le immagini del triangolo e del cerchio rappresentano un cono
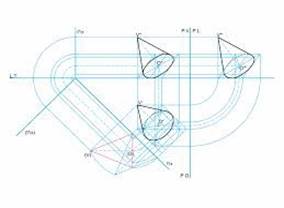
in generale, saranno presenti più immagini dello stesso oggetto, generate da proiezioni su diversi piani poi sovrapposti sul foglio da disegno

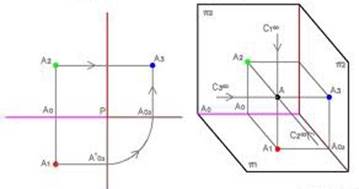
IL PUNTO
il punto è noto quando siano note due delle sue proiezioni sui piani coordinati

LA RETTA
una retta è nota quando sono noti due dei suoi punti
i punti di intersezione tra la retta ed i piani coordinati prendono il nome di tracce
IL PIANO
un piano è noto quando sono note due rette che gli appartengono

le rette di intersezione tra il piano ed i piani coordinati prendono il nome di tracce
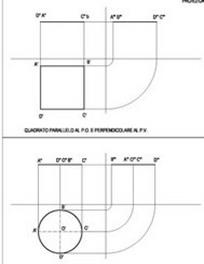
solo in casi particolari si potranno disegnare direttamente le figure in esame:
in generale, queste risulteranno deformate in entrambe le proiezioni
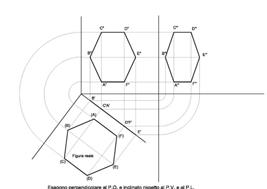
si renderà necessario eseguire il ribaltamento
dei piani che le contengono
(piani accessibili all’operatore)
operazione che porta il piano a a sovrapporsi a b mediante una rotazione rigida attorno alla loro retta intersezione

nelle proiezioni ortogonali, il piano viene portato a sovrapporsi ad uno dei quadri di riferimento mediante una serie di procedimenti planari
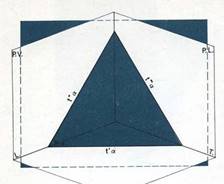
PROIEZIONI ORTOGONALI
VERE GRANDEZZE
raddrizzamento
si utilizza un piano verticale ausiliario avente la prima traccia ortogonale a quella del piano da ribaltare:

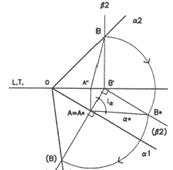
 ribaltamento tramite la RMP
ribaltamento tramite la RMP
ribaltamento diretto della
seconda traccia
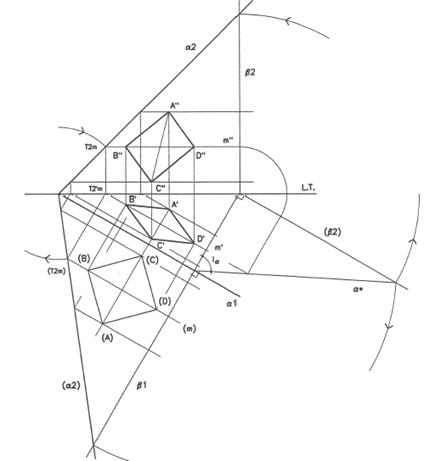
ribaltamento (mediante RMP) per disegnare la base del solido
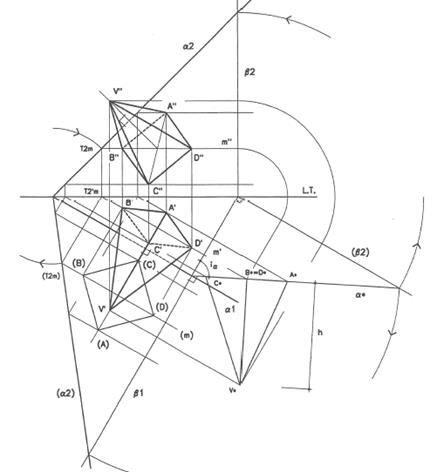
utilizzo della RMP per staccare l’altezza del solido
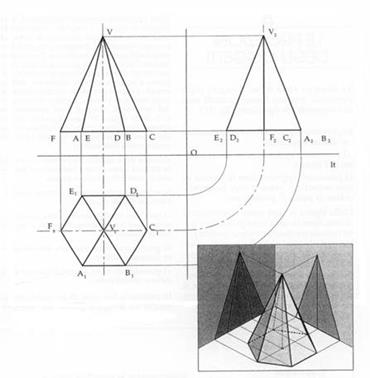
un solido avente la base sul piano orizzontale viene detto in posizione elementare
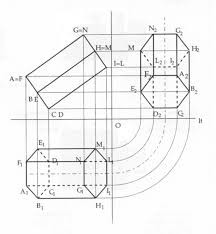
è possibile disegnare direttamente il solido solo quando questo è disposto in posizioni particolari rispetto ai piani coordinati...
... alle quali si può arrivare, dalla posizione elementare, tramite una serie di rotazioni

in generale, ci si riconduce a tali posizioni tramite opportune
proiezioni su piani diversi da quelli coordinati, di solito verticali, a utilizzarsi quali
passaggi intermedi
per leggervi le vere grandezze e risolvere i problemi di posizionamento dei solidi
relativamente alla grafica, si notino 3 distinti tipi di linea:
in ogni proiezione, è sempre marcato il contorno apparente del solido, ovvero il perimetro della figura che rappresenta il solido in quella particolare vista
per capire se le linee interne rappresentino spigoli visibili oppure nascoste, occorre invece coordinare le informazioni date da due diverse immagini:

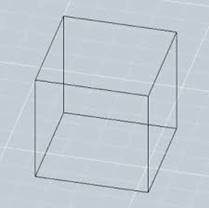
NO SI
con una sola immagine, non è possibile capire quali linee vadano marcate e quali, invece, tratteggiate
una superficie si dice sviluppabile quando può essere distesa su di un piano senza subire distorsioni

devono essere delimitati da facce piane (solidi prismatici) e/o superfici a semplice curvatura (coni e cilindri)

sviluppo di solidi prismatici

la vera grandezza delle facce dei solidi prismatici può trovarsi ribaltando il piano
a cui queste appartengono
sviluppo di piramide a base triangolare

coni e cilindri, anche sezionati, possono svilupparsi esaminando un numero significativo di generatrici appartenenti
alla loro superficie laterale
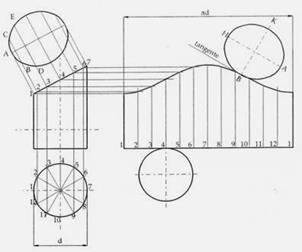
sviluppo di cono
sviluppo di cilindro

la figura intersezione tra un solido ed un piano può trovarsi applicando 3 distinte metodologie:
(ad es., retta / piano)
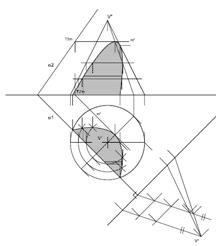
(di solito, orizzontali)
sezioni ausiliarie orizzontali
uso della RMP
qui si parrà la tua nobilitate (INF, II, 9)
il problema delle intersezioni tra i solidi può considerarsi un compendio di quanto esposto sinora, perchè può sempre ricondursi ad un insieme di costruzioni elementari
si può pertanto mettere in evidenza una ben precisa metodologia di risoluzione
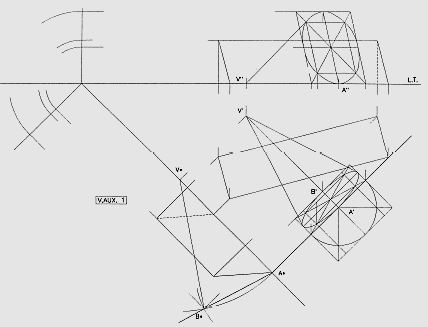
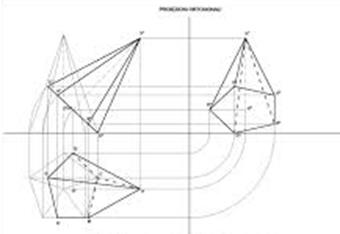
costruzione dei solidi
per disegnare il cono, è stato necessario costruire la vista ausiliaria 1; il prisma è invece in posizione elementare
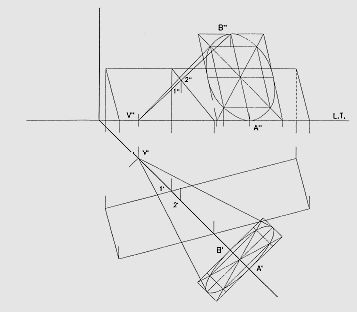
ricerca dell’intersezione
scomposizione del solido (cono) in elementi semplici (rette generatrici)
i punti di intersezione delle generatrici con il prisma possono ricercarsi tramite piani verticali ausiliari

ricerca dell’intersezione
utilizzo di altre viste ausiliarie
in alternativa, può costruirsi una vista ausiliaria che mostri come proiettante la superficie laterale del prisma
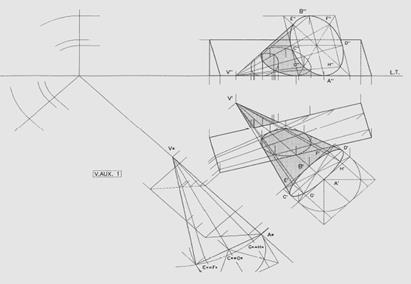
ricerca dell’intersezione
ricercata l’intersezione, i solidi vengono colorati per verificare la correttezza della soluzione
(condizione necessaria ma non sufficiente)
Fonte: https://www.unipi.it/index.php/documenti/item/download/2347_93cda8bf0ed0db5a229a3451739b694b
Sito web da visitare: https://www.unipi.it
Autore del testo: Nocera
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve