I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Enunciato:
Se la funzione 
è continua nell’intervallo chiuso 
e derivabile internamente ad esso, allora esiste almeno un punto di ascissa 
, interno all’intervallo, in cui l’incremento della funzione relativo all’intervallo 
è uguale al prodotto tra l’ampiezza dell’intervallo e la derivata della funzione calcolata in quel punto, ossia:
Esercizio :
Controllare se la funzione 
, nell’intervallo chiuso 
verifica le ipotesi del Teorema di Lagrange e in caso affermativo, calcolare l’ascissa dei punti che verificano il teorema.
La funzione 
è una funzione algebrica razionale intera di terzo grado, parabola cubica, quindi è continua nell’intervallo chiuso 
e derivabile (
) nei punti interni di questo intervallo, pertanto, esiste almeno un punto di ascissa 
, interno all’intervallo, in cui l’incremento della funzione relativo all’intervallo, cioè 
, è uguale al prodotto tra l’ampiezza dell’intervallo, ossia 
, e la derivata calcolata in quel punto, ossia 
, infatti, si ha: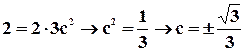 
.
Quindi i punti 
e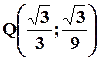 
verificano il Teorema di Lagrange.
Osservazioni:
il Teorema di Lagrange, geometricamente, si interpreta dicendo:
se un arco di curva continua è dotato di tangente in ogni suo punto, esclusi al più gli estremi, esiste almeno un punto interno all’arco nel quale la tangente è parallela alla corda che congiunge i punti estremi dell’arco.
Fonte: http://www.maurolabarbera.it/Lagrange.doc
Sito web da visitare: http://www.maurolabarbera.it
Autore del testo: non indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve