Carga y descarga de un condensador
Los resúmenes, toma nota de los textos que figuran en nuestra página web se ponen a disposición de forma gratuita con fines didácticos de la ilustración, científica, social, civil y cultural a todos los posibles interesados de acuerdo con el concepto de uso justo, y con el 'objetivo de cumplimiento de la Directiva Europea 2001/29 / CE y del «arte. 70 de la ley 633/1941 sobre derechos de autor
La información médica y de la salud en este sitio es de carácter general y para propósitos informativos solamente y por lo tanto no puede en ningún caso sustituir el consejo de un médico (o un autorizado legalmente a la profesión).
Carga y descarga de un condensador
Proceso de carga:
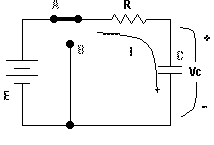
Cuando el interruptor se mueve a A, la corriente I sube bruscamente (como un cortocircuito) y tiene el valor de I = E / R amperios (como si el condensador no existiera momentáneamente en este circuito serie RC), y poco a poco esta corriente va disminuyendo hasta tener un valor de cero (ver el diagrama inferior).
El voltaje en el condensador no varía instantáneamente y sube desde 0 voltios hasta E voltios (E es el valor de la fuente de corriente directa conectado en serie con R y C, ver diagrama 1).
El tiempo que se tarda el voltaje en el condensador (Vc) en pasar de 0 voltios hasta el 63.2 % del voltaje de la fuente está dato por la fórmula T = R x C donde R está en Ohmios y C en Milifaradios y el resultado estará en milisegundos.
Después de 5 x T (5 veces T) el voltaje ha subido hasta un 99.3 % de su valor final
Al valor de T se le llama "Constante de tiempo"
Analizan los dos gráficos se puede ver que están divididos en una parte transitoria y una parte estable. Los valores de Ic y Vc varían sus valores en la parte transitoria (aproximadamente 5 veces la constante de tiempo T), pero no así en la parte estable.
Los valores de Vc e Ic en cualquier momento se pueden obtener con las siguientes fórmulas:
Vc = E + ( Vo - E) x e-T/ t ,
Vo es el voltaje inicial del condensador (en muchos casos es 0 Voltios)
Ic = ( E - Vo ) x e-T/ t / R
Vo es el voltaje inicial del condensador (en muchos casos es 0 Voltios)
VR = E x e-T/ t Donde : T = R x C

Proceso descarga:
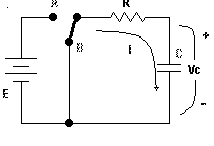
El interruptor está en B.
Entonces el voltaje en el condensador Vc empezará a descender desde Vo (voltaje inicial en el condensador). La corriente tendrá un valor inicial de Vo / R y disminuirá hasta llegar a 0 (cero voltios).
Los valores de Vc e I en cualquier momento se pueden obtener con las siguientes fórmulas:
Vc = Vo x e-t / T I = -(Vo / R) e-t / T
Donde: T = RC es la constante de tiempo
NOTA: Si el condensador había sido previamente cargado hasta un valor E, hay que reemplazar Vo en las fórmulas con E

Carga de un condensador
Considérese el circuito en serie de la figura. Inicialmente el condensador está descargado. Si se cierra el interruptor I la carga empieza a fluir produciendo corriente en el circuito, el condensador se empieza a cargar. Una vez que el condensador adquiere la carga máxima, la corriente cesa en el circuito.
En el circuito de la figura tendremos que la suma
Vab+Vbc+Vca=0
 |
- El extremo a tiene un potencial mayor que el extremo b de la resistencia R ya que la corriente fluye de a a b. De acuerdo a la ley de Ohm Vab=iR
- La placa positiva del condensador b tiene mayor potencial que la placa negativa c, de modo que Vbc=q/C.
- El terminal positivo de la batería a tiene mayor potencial que el terminal negativo c, de modo que Vca=-Ve , donde Ve es la fem de la batería
|
La ecuación del circuito es
iR+q/C-Ve =0
Teniendo en cuenta que la intensidad se define como la carga que atraviesa la sección del circuito en la unidad de tiempo, i=dq/dt, tendremos la siguiente ecuación para integrar
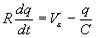

Derivando con respecto al tiempo, obtenemos la intensidad en función del tiempo
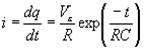
La carga tiende hacia un valor máximo C·Ve al cabo de un cierto tiempo, teóricamente infinito.
La intensidad disminuye exponencialmente con el tiempo, hasta que se hace cero cuando el condensador adquiere la carga máxima.
La cantidad RC que aparece en el denominador de t se denomina constante de tiempo del circuito. Este representa el tiempo que tomará a la corriente para decrecer hasta 1/e de su valor inicial.
Un tubo-capilar alimentado por un flujo constante producido por un frasco de Mariotte es la analogía hidráulica de la carga de un condensador.
Balance energético
- La energía aportada por la batería hasta el instante t es

- La energía disipada en la resistencia hasta el instante t es
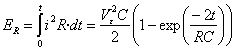
- La energía almacenada en el condensador en forma de campo eléctrico es
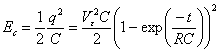
Comprobamos que Eb=ER+EC. Parte de la energía suministrada en la batería se disipa en la resistencia, y otra parte se acumula en el condensador.
Cuando se completa el proceso de carga t→∞, la mitad de la energía suministrad por la batería se disipa en la resistencia y la otra mitad se acumula en el condensador.
Ejemplo:
Sea un condensador de capacidad C=1.5 mF en serie con una resistencia de R=58 kW y una batería de Vє=30 V. Empecemos a contar el tiempo cuando se cierra el interruptor. En el instante t=60 ms
- La carga del condensador es
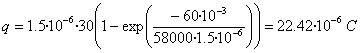
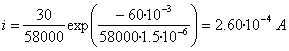
- La energía suministrada por la batería es

- La energía disipada en la resistencia es
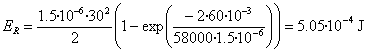
- La energía acumulada en el condensador es

Cuando se completa el proceso de carga t→∞,
- La carga del condensador es
q=CVє=1.5·10-6·30=45μC
- La energía suministrada por la batería es
Eb=13.5·10-4 J
- La energía acumulada en el condensador es
Ec=6.75·10-4 J
- La energía total disipada en la resistencia es
ER=6.75·10-4 J
:
Actividades
Se introduce
- La capacidad C del condensador, actuando sobre la barra de desplazamiento titulada Condensador
- La resistencia R, actuando sobre la barra de desplazamiento titulada Resistencia
- La fem Vede la batería está fijada en el valor de 10
Se pulsa el botón titulado Empieza
Se observa la carga del condensador, su color pasa gradualmente de blanco (sin carga) a rojo (carga positiva) y azul (carga negativa). A la derecha del applet, se traza la gráfica de la carga q y de la intensidad i en función del tiempo.
Observar
- que la carga máxima no depende de la resistencia R,
- que la intensidad máxima no depende de la capacidad C
Elegir dos valores de la resistencia R1 y R2 y dos valores de la capacidad C1 y C2 de modo que R1·C1=R2·C2. |
LineasApplet aparecerá en un explorador compatible JDK 1.1 |
|
|
Descarga de un condensador
Consideremos ahora el circuito que consta de un condensador, inicialmente cargado con carga Q, y una resistencia R, y se cierra el interruptor I.
La ecuación del circuito será la siguiente.
Vab+Vba=0
 |
- Como la corriente va de a hacia b, el potencial de a es más alto que el potencial de b. Por la ley de Ohm Vab=iR.
- En el condensador la placa positiva a tiene más potencial que la negativa b, de modo que Vba=-q/C.
|
La ecuación del circuito es
iR-q/C=0
Como la carga disminuye con el tiempo i=-dq/dt. La ecuación a integrar es

La carga del condensador disminuye exponencialmente con el tiempo. Derivando con respecto del tiempo, obtenemos la intensidad, en el sentido indicado en la figura.
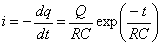
que disminuye exponencialmente con el tiempo.
La descarga tubo-capilar es la analogía hidráulica de la descarga del condensador.
Balance energético
- La energía inicial del condensador es

- La energía disipada en la resistencia hasta el instante t es
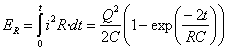
- La energía almacenada en el condensador en forma de campo eléctrico en el instante t es
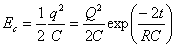
Comprobamos que Ec=E0-ER. La energía en el condensador se disipa en la resistencia. Cuando se completa el proceso de descarga t→∞, toda la energía almacenada en el condensador se ha disipado en la resistencia
Ejemplo:
Sea un condensador de capacidad C=1.5 mF en serie con una resistencia de R=58 kW cargado inicialmente con Q=45μC. Empecemos a contar el tiempo cuando se cierra el interruptor. En el instante t=60 ms
- La carga del condensador es

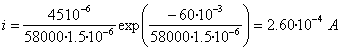
- La energía almacenada inicialmente en el condensador es
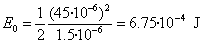
- La energía disipada en la resistencia es

- La energía acumulada en el condensador es
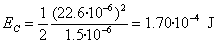
Actividades
Se introduce
- La capacidad C del condensador, actuando sobre la barra de desplazamiento titulada Condensador
- La resistencia R, actuando sobre la barra de desplazamiento titulada Resistencia
- La carga inicial Q del condensador se ha fijado en el programa
Se pulsa el botón titulado Empieza
Se observa la descarga del condensador, su color pasa gradualmente de rojo (carga positiva) y azul (carga negativa) a blanco (descargado) . A la derecha del applet, se traza la gráfica de la carga q y de la intensidad i en función del tiempo.
Elegir dos valores de la resistencia R1 y R2 y dos valores de la capacidad C1 y C2 de modo que R1·C1=R2·C2. Observar como decrece la carga y la intensidad. |
LineasApplet aparecerá en un explorador compatible JDK 1.1 |
|
|
Carga y descarga de un condensador

|
Cuando el circuito RC se conecta a un generador de señales cuadradas, podemos observar en un osciloscopio el proceso de carga y descarga. |
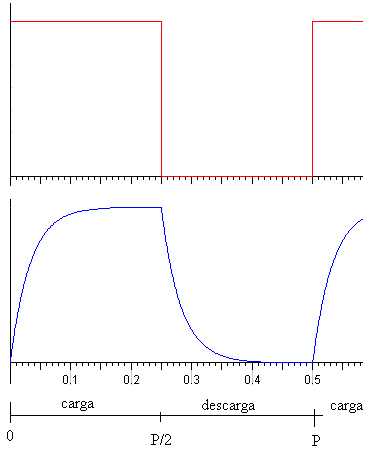
Como se ve en la figura, durante el primer semiperiodo de la señal la fem tiene un valor constante e igual a V0. El condensador se carga durante un tiempo P/2.
La carga q1 final del condensador en el instante t=P/2 se calcula a partir de la fórmula

En el instante t=P/2 la fem se hace cero, el condensador se descarga. La carga del condensador q2 en el instante t=P se calcula a partir de la fórmula,

En el siguiente proceso de carga, la integración no es entre los límites 0 y q, sino entre la carga remanente q2 y q.

Calculamos la carga final q3 en el instante t=P+P/2. Y así, sucesivamente.
Actividades
La carga y descarga del condensador la podemos observar, introduciendo una señal cuadrada en el circuito RC, y haciendo llegar la señal resultante a un osciloscopio.
Se introducen los siguientes datos
- La resistencia R en W
- La capacidad C en mF (10-6 F)
- La fem Ve , en V
- La frecuencia f en Hz de la señal cuadrada. El periodo P es la inversa de la frecuencia, P=1/f . Por ejemplo, si la frecuencia es 2000 Hz el periodo es 0.0005 s ó 0.5 ms (milisegundos)
Se pulsa el botón titulado Gráfica |
Fuente del documento: http://iesparearques.net/tecno/Bloques%20de%20Contenidos%20agost%202011/Electronica/Documents/2-%20condensadors/Carga%20y%20descarga%20de%20un%20condensador.doc
Sitio para visitar: http://iesparearques.net/
Autor del texto: no especificado en el documento de origen o se indique en el texto
Las letras son propiedad de sus respectivos autores y les damos las gracias por la oportunidad que nos brindan para conocer sus textos libres para fines ilustrativos y educativos. Si usted es el autor del texto y que está interesado para solicitar la eliminación del texto o la inserción de otra información envíe un correo electrónico después de que los controles adecuados que va a satisfacer su solicitud tan pronto como sea posible.
Carga y descarga de un condensador
Los resúmenes, toma nota de los textos que figuran en nuestra página web se ponen a disposición de forma gratuita con fines didácticos de la ilustración, científica, social, civil y cultural a todos los posibles interesados de acuerdo con el concepto de uso justo, y con el 'objetivo de cumplimiento de la Directiva Europea 2001/29 / CE y del «arte. 70 de la ley 633/1941 sobre derechos de autor
La información médica y de la salud en este sitio es de carácter general y para propósitos informativos solamente y por lo tanto no puede en ningún caso sustituir el consejo de un médico (o un autorizado legalmente a la profesión).
Carga y descarga de un condensador



