Osciladores

 

Introducción

El oscilador es un generador electrónico de señales, y es el circuito que convierte la fuente de DC en señal de AC. Se usa ampliamente en las comunicaciones inalámbricas, dispositivos de cálculo, y en la mayoría de los instrumentos y equipo de control en ingeniería. Por lo tanto, el oscilador juega un papel muy importante en la fabricación de instrumentos electrónicos. Los osciladores han realizado el cambio de los circuitos con tubos al vacío hacia los circuitos integrados (IC) con el desarrollo de las nuevas tecnologías. Sin embargo, la forma básica de operación no ha variado. Según el tipo de salida que se requiera, los osciladores se pueden clasificar como senoidales y no senoidales.
En la Sección 16.1 comenzaremos a estudiar el concepto básico de la oscilación, realimentación positiva, condiciones requeridas por los criterios de Barkhausen, y la estructura básica del oscilador. En la Sección 16.2 veremos los osciladores senoidales, incluyendo aquellos de variación de fase para circuitos osciladores de baja frecuencia, el oscilador de puente Wien, y el oscilador de doble T. Para circuito de oscilación de alta frecuencia, veremos el oscilador Colpitts, el Hartley, y el Clapp, así como el caso particular del oscilador de cristal. Finalmente, en la Sección 16.3 veremos los osciladores no senoidales, que son los multivibradores astables, multivibradores monoestables, y biestables, el disparador Schmitt, oscilador de bloqueo, generador de ondas en diente de sierra y de ondas triangulares.

 

•    Concepto básico de oscilación

En esta sección discutiremos el principio básico y las condiciones de operación del oscilador. Comencemos en la Sección 16.1.1 sobre realimentación positiva, luego el criterio de Barkhausen en la Sección 16.1.2, y finalmente veremos la estructura básica del oscilador en la Sección 16.1.3.

 

16.1.1    Realimentación Positiva

En el circuito de amplificación se envían señales parciales de salida hacia el terminal de entrada, lo cual se llama “realimentación”. La realimentación afecta las señales de salida del circuito amplificador. En la Fig. 16.1, señales parciales de salida (Vo) se realimentan al terminal de entrada y se combinan con la señal de entrada (Vs), para luego ser alimentadas al circuito de amplificación.
Asumiendo que la ganancia de tensión del circuito de amplificación es A, la relación de realimentación se expresa como b. Por lo tanto, se puede obtener la tensión de salida Vo = Avi. Después del circuito de realimentación, la tensión de realimentación es Vf = bVo. Por lo tanto la señal de entrada Vi = Vf + Vs, Vs = Vi – Vf = Vi - bVo. La ganancia de tensión de realimentación Af para todo el circuito es:

 

            

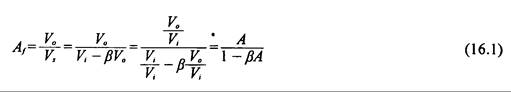
De esta ecuación sabemos que cuando bA es negativo, el denominador 1-bA es mayor que 1, lo cual produce que Af < A. Este tipo de realimentación se  llama realimentación negativa, y limita la ganancia del circuito de amplificación. Cuando bA = 0, Af = A y no habrá realimentación. Cuando bA es positivo, el denominador 1-bA es menor que 1, lo que produce que Af > A. Este tipo de realimentación se  llama realimentación positiva, y aumenta la ganancia del circuito de amplificación.

                          

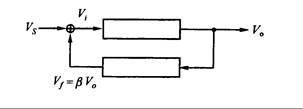
Fig. 161. Circuito de Retroalimentación

Para la realimentación positiva, las señales de salida se mejoran de nuevo al pasar cada vez por el circuito de realimentación. Como resultado, la señal de salida se hace cada vez más fuerte, y cuando es los suficientemente fuerte alcanza la región de características de no – linearidad de los dispositivos  activos en el circuito, por lo cual la señal de salida se distorsiona.
Cuando bA = 1, el denominador de la Ecuación (16.1) se aproxima a cero y la ganancia de realimentación Af llega a ser ilimitada.

            
El caso real de este caso es el sistema de altavoces. Cuando el micrófono se encuentra muy cerca de los parlantes, cualquier señal pequeña interrumpida producirá ruido.

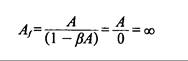
16.1.2    Criterio de Barkhausen

En la sección anterior hemos mencionado que cuando bA = 1, el denominador en la Ecuación (16.1) se aproxima a cero y la ganancia Af es ilimitada. Si no hay señal de entrada en el terminal de entrada (Vs), como lo muestra la Fig. 16.2, la señal del circuito amplificador se realiza por la realimentación en el terminal de salida. Por lo tanto, no interesa de dónde proviene la señal (esta señal puede ser ruido generado en el circuito o distribuido por el ambiente externo), pues siempre será amplificada. Luego, pasa por el circuito de re – alimentación y de nuevo hacia el de amplificación sin que haya pérdida. A esta situación de bA = 1 como “criterio de Barkhausen”

 

 

  

                        
Fig. 16.2 – Diagrama de bloques del oscilador

 

En un oscilador, la tensión de salida es igual a la señal de entrada y se convierte en la señal original, la cual se considera como oscilación. Para el diseño de un amplificador u oscilador es necesario tomar  en cuenta el criterio de Barkhausen, que es el que induce la oscilación innecesaria, y se requiere  asegurarse de que el mismo se puede alcanzar para propósitos de oscilación.

Para lograr la oscilación, los dispositivos a menudo se diseñan con un bA ligeramente mayor de 1, siendo la principal razón que así se asegura que la señal de realimentación es mayor que la señal previa. Si esta situación se prolonga, habrá una salida ilimitada de tensión.

 

La curva característica del circuito de amplificación es lineal en la región normal, pero una vez que la tensión de entrada se sale del límite particular que se le dé, el punto de operación cambiará hacia la región de saturación o de corte. Esto hará que A desminuya de nuevo, y finalmente bA será igual a 1.

 

 

16.1.3    Oscilador Básico

La Fig. 16.3 muestra el circuito de oscilación que satisface el criterio de Barkhausen. Este circuito es el par de capacitores de dos etapas y el amplificador de emisor común con 100% de realimentación. Su ganancia A es un valor positivo. Cuando A se eleva mucho inducirá la oscilación.

Sin embargo, la señal de entrada no es una onda senoidal, por lo que solamente sabemos que se trata de una oscilación por el criterio de Barkhausen. Sin embargo no se puede garantizar que la salida sea una onda senoidal, y para obtener una onda de este tipo es necesario un circuito adicional que la genere.

 

 

 

 
Fig. 16.3 Circuito oscilador básico

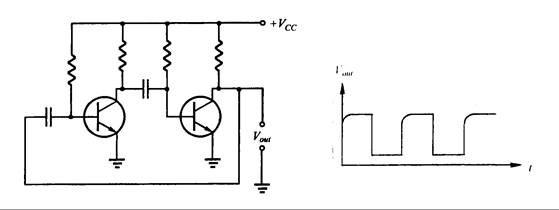
Con una entrada puramente senoidal, es necesario usar el Teorema de Fourier, que enuncia que una onda repetible y compleja está compuesta de muchas ondas senoidales básicas. Por lo tanto, si agregamos un filtro en el terminal de entrada del amplificador, obtenemos una salida de onda senoidal. De lo que previamente hemos aprendido sobre electricidad básica, sabemos que la impedancia de un inductor y de un capacitor es muy sensible a la frecuencia. Por lo tanto, se utiliza el inductor y el capacitor para ajustar la onda de salida y controlar la frecuencia de salida del oscilador.

  

            

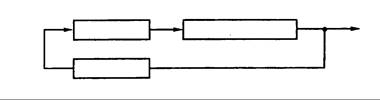
Fig. 16.4 – Diagrama de bloques del oscilador, donde se aprecian los circuitos de frecuencia y de onda.

En el circuito LC serie de la Fig. 16.5,  la impedancia total es XL – XC. Cuando XL = XC, la impedancia total es cero. La frecuencia cuando XL = XC se le conoce como frecuencia resonante del circuito.

Una vez que el circuito LC se empieza a usar, la frecuencia de resonancia es fácil de pasar hacia el circuito LC en serie y realimentar el terminal de entrada del amplificador. Para otras frecuencias el circuito LC serie se bloquea.

Por lo tanto, el oscilador se puede diseñar como un circuito LC serie y usar la condición de frecuencia de resonancia bA = +1 para recibir la salida de onda senoidal. La frecuencia de resonancia es como se indica en la Ecuación (16.2):

            

 Cuando        

Fig. 16.5. Circuito serie LC                            Fig. 16.6. circuito serie RLC
con resistencia   interna en el inductor

En el inductor se tiene una resistencia interna, como lo muestra el circuito serie LC de la Fig. 16.6. Por lo tanto, la impedancia total de la frecuencia resonante es R, y la resistencia interna del inductor afectará las características inductivas del circuito. Por ello, definimos el valor Q como Q = X1 / R, indicando el valor alto de Q que hay una resistencia interna más baja en el inductor, y por lo tanto funcionará como inductor ideal.
La Fig. 16.7 (a) muestra el circuito LC paralelo ideal, donde la impedancia total de resonancia es Zt = -[(XLXC / (XL – XC)]. Cuando XL = XC , está en resonancia. Por lo tanto, la impedancia total es infinita. La Fig. 16.7(b) representa el circuito resonante paralelo real, cuya frecuencia de resonancia se calcula según la Ecuación (16.2).

                          

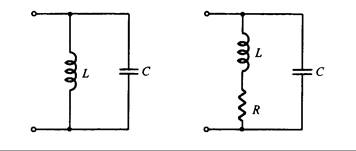
                        (a) Circuito LC paralelo             (b) circuito LC paralelo equivalente

Fig. 16.7 – Circuito LC paralelo

 

Ejemplo 16.1. Un inductor de 100 mH y un capacitor se conectan juntos en serie como circuito resonante, cuya frecuencia de resonancia es de 1000 Hz. Determine la capacitancia del capacitor.

 

Respuesta:

            

•     Oscilador Senoidal

 

En esta sección veremos el oscilador senoidal. En la sección 16.2.1 veremos el oscilador variador de fase, que se compone de un oscilador de baja frecuencia con una resistencia (R ) y un capacitor (C).  En la Sec. 16.2.2 veremos el oscilador puente Wien, y en la Sec. 16.2.3 el oscilador de doble T. Un oscilador de alta frecuencia se compone de un inductor (L) y un capacitor (C). Veremos el oscilador Colpitts en la Sec. 16.2.4, el oscilador Hartley en la Sec. 16.2.5, y el oscilador Clapp en la Sec. 16.2.6. Finalmente veremos el oscilador de cristal en la Sec. 16.2.7

• Oscilador Variador de Fase

 

Un oscilador de realimentación positiva debe satisfacer las siguientes dos condiciones:

1. Debe tener realimentación positiva, para que no exista diferencia de fase entre la señal de realimentación y la señal de entrada.
2. El producto de la ganancia total y la realimentación debe ser 1 (es decir, según el criterio de Barkhausen, bA = +1). Esto hace que funcione la oscilación.

En la Fig. 16.8, el amplificador del oscilador variador de fase en el diagrama de bloques es un circuito a transistores de etapa única. Su señal de entada tiene 180º de diferencia con respecto a la señal de salida. Bajo ciertas frecuencias de resonancia, la señal de salida debe tener una variación de fase de 180º después de pasar por la red de variación de fase, ya que se realimentará en el terminal de entrada. Se satisface así la variación de fase de 0º requerida para la realimentación positiva. Si la ganancia del amplificador es Av, entonces deberá haber una pérdida de menos de 1 / Av en la red de variación de fase para mantener la oscilación. Existen dos tipos de variación de fase para la red resistencia – capacitor de variación de fase, uno de ellos es la red de compensación de adelanto y la otra es la red de compensación de atraso.

  

   

La Fig. 16.9(a) muestra la red de compensación de adelanto. La tensión de entrada Vi que pasa por el capacitor C permitirá que la corriente I adelante a la tensión en un ángulo q. La corriente que fluye a través de la resistencia producirá una tensión Vo de salida, y por lo tanto este Vo irá también delante del ángulo Viq, según se muestra en la Fig. 16.9(b).

 

                          

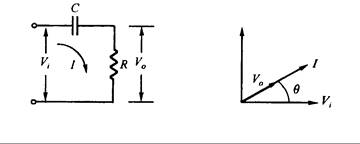
(a) Red RC con adelanto             (b) Diagrama de fases de V e I
en el circuito de adelanto   

Fig. 16.9 -  Red de adelanto

La Fig. 16.10(a) muestra la red de atraso. La tensión de entrada Vi que fluye por la resistencia y el capacitor dejará que la corriente delante a la tensión, y provocará que Vo se atrase con respecto a Vi. Cuando I se adelanta a Vi con un ángulo a, la tensión en C se atrasará 90º con respecto a la corriente. Por lo tanto, Vo va detrás de Viq = 90º - a, como se muestra en la Fig. 16.10(b).

                        
                       
(a) Red RC con retraso               (b) Diagrama de fases de V e I
                                                                  en el circuito de atraso

Fig. 16.9 -  Red de retraso

 

Para obtener la variación de fase de 180º, se puede usar la red RC de tres etapas para crear la red de adelanto, Fig. 16.11(a), o la red de atraso, Fig. 16.11(b).

 

 

 

 

           

 

Resolviendo estas ecuaciones obtenemos el siguiente resultado para i3:

 

 

 

           

 

Por lo tanto, para las tres etapas de realimentación de la red RC de variación de fase, la frecuencia resonante fo = 1 / (2p RC Ö6)
La ganancia del amplificador debe ser por lo menos de 29.

 

 

 

              

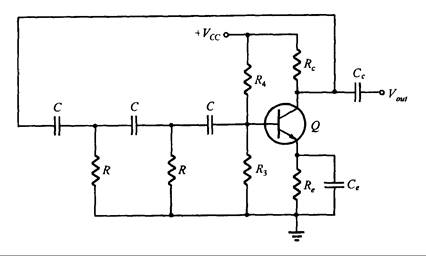
Fig.16.13 – Oscilador RC con variación de fase

 

En la Fig.16.13, el oscilador RC con variación de fase, R3, R4 y la impedancia de entrada hie están conectadas en paralelo formando la resistencia R. Cuando la ganancia de realimentación de todo este circuito es mayor que 1, habrá una sobrecarga y la onda tendrá una forma cuadrada. Generalmente el oscilador RC con variación de fase se usa en audio-frecuencia. A veces no es fácil ajustarlo en el rango de frecuencias anchas.

 

Ejemplo 16.2. En la Fig.16.13, C=1000pF, R=10kW, R3 //R4 //hie = 10kW. Determine la frecuencia de oscilación.

 

Respuesta: De acuerdo con la ecuación (16.3), la frecuencia de oscilación es:

            

 

• Osciladores de puente Wien

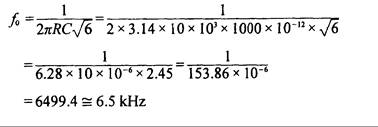
El puente Wien puede usarse en osciladores estándar de frecuencia baja / mediana (5Hz – 1MHz). Generalmente se usa para generadores de audio de tipo comercial u otras aplicaciones en baja frecuencia

 

 

El oscilador de puente Wien se usa en circuitos de compensación por adelanto o por retraso como circuito de realimentación, como se muestra en la Fig.16.14. En frecuencias muy bajas, el capacitor en serie puede considerarse como circuito abierto para la señal de entrada, por lo tanto no habrá salida Vout. En frecuencias muy altas, el capacitor paralelo puede considerarse como en cortocircuito, pero todavía no se generará Vout. Entre estas dos frecuencias extremas Vout cambiará según la frecuencia. En la frecuencia de resonancia fo, se tiene la salida máxima y el ángulo de fase es 0º. En condiciones más altas ó más bajas que la frecuencia de resonancia la salida de realimentación será más baja que el máximo y el ángulo de fase no será 0º.

  

                  

  

 

 

La Fig.16.15 representa la estructura básica del oscilador de puente Wien, donde los circuitos R1C1 y R2C2 que están en paralelo, se conectan como red de realimentación positiva. Puede suministrar diferentes realimentaciones positivas Vf1 para diferentes frecuencias, y determina la frecuencia resonante. R3 y R4 se conectan como red de realimentación negativa, suministra la realimentación negativa Vf2, y determina la ganancia del circuito y estabiliza la amplitud de la salida. Para funcionar como circuito oscilador, debe ser satisfecha con el criterio de Barkhausen, bAv = 1, pues de lo contrario no se reproduce oscilación. Cuando la red de puente está en equilibrio Vi = Vab = 0 , y b = Vab / Vcd = 0 . La ganancia de realimentación se convierte en bAv = 0 . Esto contradice la condición de oscilación bAv = 1 y por lo tanto el puente tiene que funcionar en estado de no equilibrio para que haya oscilación. Sí

 

---Ver Libro de Texto---

Cuando el puente está bajo equilibrio,

---Ver Libro de Texto---

Por lo tanto,

---Ver Libro de Texto---

En vista de que R3 / R4 es un número real, el número imaginario en la ecuación anterior debe ser igual a cero, es decir

---Ver Libro de Texto---

R2X2 no es igual a cero y por lo tanto R1R2 – X1X2 = 0

---Ver Libro de Texto---

Finalmente

---Ver Libro de Texto---

 

Refiriéndose a la frecuencia de oscilación,

---Ver Libro de Texto---

Sí: R1 = R2 = R , y C1 = C2 = C ,

f0 = 1/(2pRC)                                                                                   (16.4)

La parte real de  R3 / R4 es :

---Ver Libro de Texto---

Por lo tanto, R3 = 2R4                                                                               (16.5)

La relación entre R3 y R4 puede determinar la realimentación negativa; cuando R3 / R4 – 2, la realimentación positiva es mayor que la negativa y el circuito estará en oscilación en fr.
Cuando la red de puente de la Fig.16.15 está en equilibrio,

---Ver Libro de Texto---

Sin embargo, cuando Vad = Vbd , la oscilación no se producirá. Para obtener que bAv = 1, debe satisfacer que Vad > Vbd. Por lo tanto:

---Ver Libro de Texto---

Asumiendo:  ---Ver Libro de Texto---

Entonces:     ---Ver Libro de Texto---

 

 

Sí Av = k  y  bAv ³ 1 , se satisfará el criterio de Barkhausen. Por lo tanto al ajustar la relación entre R3 y R4 hará que el puente esté bajo estado de no equilibrio y que adquiera la tensión de realimentación para oscilación.
La Fig.16.16 es un oscilador de puente Wien típico; la salida del amplificador pasa por Cc, y las realimentaciones a la parte superior de la red del puente. Ca y Cc deben ser lo suficientemente grandes como para evitar la variación de fase de la frecuencia de oscilación. La salida de amplitud del oscilador está determinada por bAv. Sí b se mantiene constante cuando el Av aumenta, la amplitud aumentará hasta que quede limitada por la característica de no linealidad del transistor.
R3  y R4 determinan la estabilización de la amplitud. Cuando R3 y R4 sufren variaciones, b también variará. Generalmente R4 se remplaza con un bombillo de tungsteno que tenga un coeficiente positivo de temperatura. Cuando la amplitud se aumenta también lo hará la corriente a través de R4. La temperatura en el bombillo se incrementará y hará que R4 aumente. Esto producirá la realimentación negativa y hace que se disminuya la amplitud de salida hasta alcanzar un estado estable. Otro método es reemplazar R3 por una resistencia sensible a la temperatura que tenga coeficiente negativo de temperatura.

 

 

Fig.16.16 – Oscilador de puente Wien a transistores

Ejemplo 16.3.  En la Fig.16.16, cuando R1 = 50kW,  R2 = 50kW,  R3 = 250kW,  R4 = 100kW,   C1 = 0.001mF,   C2 = 0.001mF,  determine:

• Sí se trata de un oscilador; (2) Cuál es la frecuencia de oscilación.

 Respuesta:              

 

Como:            R3 / R4 = 2.5 > 2, se producirá la oscilación

 

 

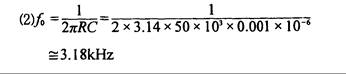
16.2.3    Oscilador Doble T

El oscilador doble T mostrado en la Fig. 16.17 es muy similar al de puente Wien. Usa un filtro T doble, cuya frecuencia de resonancia es f0 = 1 / (2pRC). La variación de fase y ganancia de tensión para resonancia son ambas 0.

                        

Fig. 16.17 – Filtro doble T

La Fig. 16.18 muestra la estructura de un oscilador doble T, donde la realimentación positiva se puede obtener de R1 y R2. Luego, se envía al terminal no invertible del amplificador. La realimentación negativa se envía a la terminal invertible del amplificador mediante un filtro doble T. Generalmente se usa para R1 un fusible de luz con coeficiente positivo de temperatura.

Cuando se enciende la fuente de tensión, R1 es muy débil, y se tiene casi solamente realimentación positiva b = 1 . Cuando se producen las señales de oscilación, R1 aumenta gradualmente y hace que disminuya la realimentación positiva. Una vez que se alcanza un equilibrio, se tiene un estado estable.

La resistencia R/2 en el filtro doble T es ajustable, y se puede usar como sintonizador fino de frecuencia. Para cerrar la brecha de frecuencia, R1 debe ser mucho más grande que R2, y R1/R2 estar entre 10 y 1000.

 

 

El oscilador doble T no se usa a menudo ni es muy común, puesto que puede funcionar únicamente bajo ciertas frecuencias. No es fácilmente ajustable como el oscilador puente Wien en el rango de las frecuencias anchas.

              

Fig. 16.18 – Estructura del oscilador doble T

 

•     Oscilador Colpitts

El oscilador RC tiene un excelente rendimiento en el rango de las frecuencias bajas. Sin embargo, no es adecuado para las frecuencias altas (especial para frecuencias mayores de 1 mHz). La principal razón es que en el amplificador se tiene variación de fase en el amplificador, y la red RC posee también variación de fase. Por lo tanto, la frecuencia real de resonancia se encuentra muy lejos de la frecuencia calculada.

La selectividad de la frecuencia LC de resonancia es muy alta, por lo que la onda senoidal es muy pura, mientras que el oscilador RC no puede alcanzar este rendimiento.

El teorema de oscilación se basa en el criterio de Barkhausen. La realimentación positiva LC tiene una variación de fase de 0º, y un bA ³ 1

La estructura general del oscilador LC se muestra en la Fig. 16.19.
Z1, Z2 y Z3 están construidos conjuntamente como red LC resonante. Aquí Z1 y Z2 son el divisor de tensión y  la realimentación de la red, proporcionándole al oscilador realimentación y variación de tensión. Si Z3 es el dispositivo inductivo, Z1 y Z2 son los dispositivos capacitivos, y se llama oscilador Colpitts.

 

 

 

                        

Fig. 16.19 – Estructura de un oscilador LC

La Fig. 16.20 muestra un oscilador Colpitts estándar, donde el circuito resonante LC se compone del circuito  L, C1 y C2 resonante en paralelo. Cuando el valor Q del circuito LC resonante es mayor de 10, la frecuencia de resonancia estará cercana a:

              

Aquí, Av es un valor aproximado, ya que no se ha considerado la impedancia de base del transistor. El Av se determina por medio de la frecuencia crítica del amplificador. Para un amplificador bipolar, existen capacitores puente en la base y en el colector. Cuando la frecuencia crítica del circuito capacitivo es mayor que la frecuencia de oscilación, Av es aproximadamente rc / r’c. Si la frecuencia crítica es menos que la frecuencia de oscilación, la ganancia de tensión es menor que rc / r’c y hay una variación adicional de fase. Esto hace que el análisis sea muy complejo, lo que dificulta la función del oscilador (puede hacerse que la variación de fase sea cero, y la ganancia de bucle menor a 1).
Para Vout, la realimentación es muy ligera (valor bajo de b) y Av es ligeramente mayor que 1/b, entonces se tiene una amplificación de clase A. Para la oscilación inicial, la señal se hace cada vez mayor en la carga AC, pero el modo de operación se  convierte en modo de señal amplia. También, Av disminuye un poco. Por lo tanto, para un realimentación ligera, bAv baja hasta 1 y no se observan fenómenos de corte de onda. Una vez que se regresa a una realimentación de mayor magnitud, la señal pondrá a funcional la base, y llevará el transistor a la región de saturación o de corte. Esto hace que C3 se cargue y produzca el enganche DC negativo en la base. bAv se ajusta automáticamente hasta llegar a 1. Sin embargo, perderá tensión en la salida debido a la pérdida de potencia.

            

Fig. 16.20 – Oscilador Colpitts

 

Durante la fabricación de un oscilador, si se ajusta la realimentación y se deja que la salida sea máxima para garantizar que se tiene suficiente realimentación de resonancia bajo cualquier condición, se puede perder la tensión de salida e inducir tensión insuficiente. Por lo tanto, el diseño de un oscilador de alta frecuencia es una tarea complicada. No se pueden utilizar las aproximaciones tradicionales para evaluarlo. En la actualidad se utiliza el cálculo por computadora para fijar un modelo de oscilador de alta frecuencia para el análisis.

La Fig. 16.20 muestra un amplificador CE a transistores de una sola etapa, donde hay una variación de fase se 180º entre la entrada y la salida. Es necesario agregar una variación de fase de 180º para llegar a la realimentación positiva. La carga en el terminal de salida es C1, y la tensión de realimentación Vf se obtiene de C2. Este Vf tiene una fase inversa con respecto a la tensión de salida Vout, y se usará para alimentar la base y satisfacer los requerimientos de realimentación positiva. El circuito CE de amplificación ofrece suficiente ganancia de tensión en la frecuencia de resonancia, siendo el valor de realimentación b de:

            

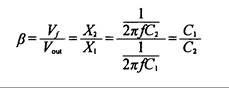
Para resonancia continua, bAv ³ 1.

            AvC1 / C2  1, y por lo tanto, Av  C2 / C1                                               (16.8)

En la Fig. 16.20, R1 y R2 proporcionan el trabajo de polarización al transistor; R3 es la resistencia del emisor como realimentación negativa DC. RFC es la carga DC. El capacitor C4 de impedancia es Xc4 f 0.1 RE. El capacitor AC C3 debe ser lo suficientemente grande como para evitar a Vf sin producir variación de fase.

Ejemplo 16.4. en el circuito de un oscilador Colpitts de la Fig. 16.20, cuando L = 100 Mh, C1 = C2 = 200 pF. (1) ¿Cuál es la frecuencia de resonancia?  (2) ¿Cuál es la ganancia en el circuito a transistores?

Respuesta: (1) Según la Ecuación (16.7):

---Ver Libro de Texto---

De la Ecuación (16.6):

---Ver Libro de Texto---

• Según la Ecuación (16.8):

 

---Ver Libro de Texto---

•     Oscilador Hartley

 

En la Fig. 16.19, si Z3 es el dispositivo capacitivo, y Z1 y Z2 son los dispositivos inductivos, entonces tenemos un oscilador Hartley. La Fig. 16.21 muestra un oscilador Hartley estándar.
En la Fig. 16.21, R1 y R2 proporcionan la polarización de base para la polarización DC. R3 es la resistencia de polarización negativa DC del emisor. RFC es la carga DC, C1 y C2 se usan para aislar la etapa frontal y trasera de los circuitos DC. C3 es el capacitor de paso de realimentación negativa, lo que generalmente requiere que XC3  0.1 R3, donde el circuito LC resonante se compone del circuito paralelo L1, L2, C. Su frecuencia de resonancia es:

---Ver Libro de Texto--- 

 

                

El teorema operativo es similar al del oscilador Colpitts. Su salida Vout se aplica a L1; la tensión de realimentación Vf se obtiene a partir de L2. El Vf tiene la fase invertida con respecto a Vout y se realimenta a la base, por lo que constituye realimentación positiva para el circuito. La relación entre ganancia de tensión y realimentación es:

              

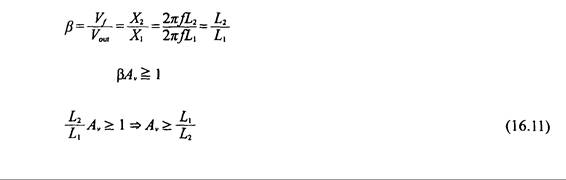
Ejemplo 16.5. La Fig. 16.21 muestra un oscilador Hartley, con C como capacitor variable. Su capacitancia se puede ajustar de 10 pF a 43 pF, y L1 = L2 = 350 mH, y M = 50 mH. ¿cuál es el rango de la frecuencia de salida del oscilador?

 

 

Respuesta: En virtud de la Ecuación (16.10), el valor de Leq es:

 

     

 

16.2.6    Oscilador Clapp

El oscilador Clapp es un oscilador Colpitts mejorado. En este último, C1 y C2 se conectan al capacitor dispersivo del transistor en paralelo, lo cual causa una pequeña variación en los valores de C1 y C2. Este fenómeno hace que la frecuencia resonante del oscilador Colpitts varíe ligeramente, mientras que en oscilador Clapp, se agrega un capacitor Cs en el bucle LC y se conecta en serie con el inductor, como lo muestra la Fig. 16.22.

            

 

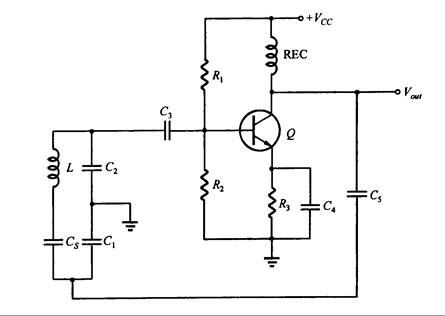
Fig. 16.22 – Oscilador Clapp

 

La Fig. 16.22 muestra un oscilador Clapp, compuesto de L, C1, C2, y Cs. Este último se diseña mucho menor que C1 y C2. En el circuito de resonancia, el capacitor C tiene una capacitancia equivalente de C1, C2 y Cs en serie, la cual es aproximadamente igual a Cs.

---Ver Libro de Texto---

La frecuencia de resonancia queda definida casi solamente por L y Cs, y es independiente de C1 y C2. Por lo tanto, los efectos de los parámetros del transistor sobre C1 y C2 casi no se notan en la frecuencia de resonancia, la cuales:

---Ver Libro de Texto---

Generalmente, la estabilización de la frecuencia de resonancia del oscilador Clapp es muy alta, y se usa mucho en receptores.

Ejemplo 16.6. En la Fig. 16.22, cuando L = 15mH, Cs = 10 pF, C1, C2 = o.1 mF. Determine la frecuencia resonante.

Respuesta: De acuerdo con la Ecuación (16.12):

---Ver Libro de Texto---

Según la Ecuación (16.13):

---Ver Libro de Texto---

16.2.7    Osciladores de Cristal

En todos los osciladores vistos anteriormente, es posible ajustar los valores RC o LC y cambiar así la frecuencia de resonancia. Sin embargo, los valores del dispositivo se cambian fácilmente debido a razones ambientales. Esto hace que la frecuencia de operación no sea estable, y por lo tanto se usan osciladores de cristal para lograr una frecuencia de trabajo estable. Sin embargo, ya no será posible ajustar libremente la frecuencia, y se requiere reemplazar los cristales para cambiar la frecuencia.

 

En la naturaleza existen algunos cristales que tienen efectos piezoeléctricos. Cuando se aplica una tensión AC en el cristal, se induce una oscilación mecánica con la frecuencia externa. Si se aplica presión mecánica sobre el cristal, también se induce tensión AC con la misma frecuencia. Este efecto piezoeléctrico del cristal es la conversión de energía mecánica en energía eléctrica. El cuarzo, la sal de Rochelle y la turmalina pueden producir efectos piezoeléctricos.

La sal de Rochelle es la que tiene efectos piezoelécticos más fuertes, pero su estructura mecánica es muy frágil y fácil de romper. Generalmente se usa en micrófonos, cabezas de grabadoras, audífonos y altoparlantes. El efecto piezoeléctrico de la turmalina es muy débil, pero su estructura mecánica es la más fuerte de los tres materiales. También su precio es el más alto. Se usa en frecuencias ultra altas. La intensidad del cuarzo está entre la sal de Rochelle y la turmalina, y es el más barato y fácil de obtener, por lo que es usado ampliamente en filtros y osciladores RF.

              

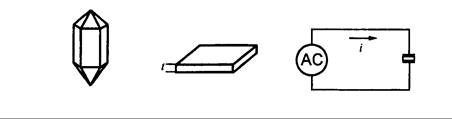
    (a) Estructura cristalina           (b) Placa plana              (c) Circuito a transistores

 

En la Fig. 16.23(a) se muestra la estructura cristalina en forma de pirámide hexagonal del cuarzo. Se corta en placas delgadas de espesor r y forma rectangular, como lo muestra la Fig. 16.23(b). Dependiendo de los diversos ángulos de corte y métodos de corte, tendrá diferentes efectos piezoeléctricos.

Generalmente existen cortes x, XY y AT. Los fabricantes por lo general ofrecen el método de corte que ofrezca el mejor efecto, de acuerdo con el producto. En un circuito electrónico, la placa plana se coloca entre dos placas metálicas, como se muestra en la Fig. 16.23(c), y debido al efecto piezoeléctrico en el circuito, el cuarzo produce una vibración mecánica. Si la frecuencia AC es igual a la frecuencia de resonancia del cristal, se induce una resonancia muy grande.

 

El tipo de corte de la superficie y el tipo de empaque harán que el cristal tenga el mejor efecto en la frecuencia de resonancia, la cual se le llama frecuencia fundamental o frecuencia mínima. En frecuencias de resonancia más altas, se le llama frecuencia armónica, que es el tiempo integral de la frecuencia fundamental. La ecuación es:

 

            

Donde k es una constante que depende del método de corte y de otros aspectos, y t es el espesor del cristal. La frecuencia fundamental es inversamente proporcional al espesor. Por ello, la alta frecuencia máxima tiene sus limitaciones, pues entre más delgado sea el cristal, será más débil y frágil, y se puede quebrar con la vibración. La frecuencia fundamental de un cristal normal puede llegar hasta los 10 MHz. En frecuencias más altas se usa la frecuencia harmónica para llegar hasta los 100 MHz, o se usa turmalina, que como sabemos, es más dura pero de precio más alto.

                          

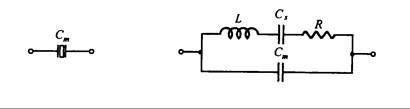
    (a) Montaje de capacitor              (b) Circuito equivalente de oscilación

Cuando el cristal no se encuentra en estado de resonancia, se asemeja a un capacitor Cm, como lo muestra la Fig. 16.24(a), que se compone de dos placas de metal como montaje para la capacitancia. Cuando el cristal vibra a la frecuencia fundamental, su circuito equivalente es tal como se muestra en la Fig. 16.24(b). El valor típico de L es solamente de unos pocos Henrios, y Cs es menos de 1 pF, mientras que R es de varios cientos de ohmios, y Cm de unos pocos pF. Estos valores se ven afectados por el método de corte, el espesor y el tipo de empaque. Los siguientes valores son típicos de parámetros para cristales: L = 3H; Cs = 0.05 pF; R = 2 kW; Cm = 10 pF.
En vista de que el cristal tiene un circuito equivalente con un alto valor de L, se tendrá un valor muy alto de Q en el bucle de resonancia. Este valor puede fácilmente llegar a 10,000. Para el oscilador, ofrece una frecuencia estable de resonancia.
El cristal tiene dos frecuencias de resonancia, una es la frecuencia de resonancia en serie. fs es la frecuencia resonante en el circuito L, Cs y R de la Fig. 16.24(b). Como L y Cs están en resonancia, la impedancia es mínima, y su frecuencia resonante es:

            

La otra es la frecuencia resonante paralela fp, que es inducida por el circuito resonante de L, Cs, R y Cm. Ver Fig. 16.24(b). Su capacitancia de bucle equivalente Cloop es Cs y Cm es la capacitancia serie.

La frecuencia resonante paralela es:

            
Cloop es la capacitancia equivalente de S y Cm en serie, cuyo valor será menor que cualquier capacitancia. Por ello, Cloop es menor que Cs y fp será más alta que fs.

Cuando el cristal se conecta al circuito resonante, como se muestra en la Fig. 16.25, Cm se verá afectada por los otros capacitores en paralelo, lo que resulta en que fp se hará más pequeño y hará que el valor de fs se haga más cercano al de fp. En resonancia serie, el cristal tiene una impedancia equivalente mínima y puede recibir la amplificación muy alta (rc equivalente es el máximo). En resonancia paralela, el cristal tiene la máxima impedancia equivalente y no tiene amplificación (rc equivalente es muy pequeño).

 

                        

Fig. 16.25 – Efecto del transistor y del capacitor dispersivo

La frecuencia de oscilación del cristal es muy estable, pero se verá afectada por la temperatura, la vida útil y otros factores. Generalmente se nota un cambio de menos de 1/106 cada día, por lo tanto es adecuado para usarlos en relojes electrónicos. Si el cristal se coloca en su empaque de temperatura controlada, se puede lograr una variación de menos de 1/1010, lo que significa un error de 1 segundo cada 300 años.

En el circuito oscilador Colpitts a transistores de la Fig. 16.26, el capacitor del divisor de tensión producirá tensión de realimentación a la base del transistor. El cristal actúa como C1 y C2 en resonancia, y la frecuencia de resonancia está entre la frecuencia resonante serie y paralelo.

 

 

 

 

• Oscilador No Senoidal

En esta sección  veremos los osciladores no senoidales. Discutiremos primero los multivibradores. En la Sección 16.3.1 se incluyen los multivibradores astables, en la Sección 16.3.2 los monoestables y el la Sección 16.3.3 los multivibradores biestables. Luego se discutirán los tipos particulares de circuito, y en la Sección 16.3.4, el disparador Schmitt. Por último veremos el oscilador bloqueador en la Sección 16.3.5, para terminar en la Sección 16.3.6 con el generador de ondas en diente de sierra y triangulares.

 

 

16.3.1    Multivibradores Astables

Colóquense dos dispositivos activos de amplificación en la región no lineal y haga que el circuito funcione alternativamente entre las regiones de corte y de saturación. Esta acción inducirá en la salida distorsiones muy serias, y como se tienen ondas multi – armónicas, excepción hecha de las ondas senoidales básicas, en la onda de salida, el dispositivo recibe el nombre de multivibrador.
Un multivibrador astable también se le conoce como multivibrador de funcionamiento libre, ya que no necesita disparar  ninguna señal para proporcionar una serie de salidas pulsantes. La Fig. 16.27 muestra un tipo de circuito multivibrador astable con conexión al colector. Se utilizan dos transistores Q1 y Q2 en el circuito, y cuando Q1 conduce, Q2 está desconectado; cuando Q2 conduce, Q1 está desconectado, cambiando alternativamente sin poder permanecer estables. Por lo tanto, se forma una serie de salidas de forma cuadrada en la salida del colector.

                        

Fig. 16.27 - Multivibrador astable

En la Fig. 16.27, Q1, Q2 y los dispositivos anexos tienen características similares. Cuando se aplica una tensión, Q1 y Q2 conducen y adquieren polarización de R1 y R2. C1 y C2 se cargan con RC1 y RC2. Los terminales cerca de los colectores tienen polaridades positivas. Sin embargo, las características de estos dos transistores no se pueden igualar por completo por lo que uno de ellos conducirá más rápido que el otro. Asumiendo que Q1 conduce más pronto que Q2, la tensión en RC1 aumentará e inducirá a que VC1 de Q1 decaiga. C1 descargará a través de R1, y el terminal más bajo de R1 tiene tensión negativa, por lo cual la base de Q2 obtiene polarización inversa en el momento de corte, como lo  muestra la Fig. 16.28(a). En este momento, VC2 » VCC, el terminal izquierdo de C2 está conectado a la tensión baja (VB1 » 0.7) de la base de Q1. Por lo tanto, C2 comienza a cargar rápidamente con VCC, como lo muestra la Fig. 16.28(b). Luego que C1 ha descargado por un tiempo, la corriente llega a ser muy baja, y la tensión negativa en el terminal inferior de R1 disminuye (VB2 disminuye). Cuando VB2 = 0.5 V, Q2 conduce e IC2 aumenta. La caída de tensión en RC2 aumenta, y VC2 disminuye (VC2 » 0.2V). Por lo tanto, C2 descarga por R2, y el terminal de abajo de R2 adquiere alta tensión negativa, y deja a Q1 en corte, Fig. 16.28(c). Q1 está en corte y VC1 » VCC. C1 se carga rápidamente con VCC, como lo muestra la Fig. 16.28(d).  Las acciones

 

anteriores se repiten en forma periódica. Los colectores proporcionan de manera periódica ondas cuadradas, como lo muestra la Fig. 16.29.

 

 

   

 

Fig. 16.28 – Caminos por donde descargan / cargan los capacitores C1 y C2

 

   

Fig. 16.29 – Forma de la onda del colector y base de Q1 y Q2

Cuando Q1 conduce, VB1 » 0.7, VR2 = VCC – VB1 = VCC – 0.7V » VCC. Cuando Q1 está en corte, el VB1 instantáneo decae a –VCC (VB1 = -VCC). La caída de tensión en R2 es 2VCC (VR2 = 2VCC). Si el tiempo de corte de Q1 es T1, ese será el tiempo requerido para VR2 desde 2VCC hasta VCC. Varía según una curva exponencial, cuyo periodo es:

                  

 

 

Cuando R1C1 no son iguales a R2C2, la salida no tiene forma de onda cuadrada simétrica. En la Fig. 16.29 se tienen ángulos redondeados en la salida de VC1 y de VC2. La razón es que, VCC cambia a C1 y C2 a través de RC1 y RC2. Para mejorar este fenómeno es necesario mejorar el bucle de carga / descarga de C1 y C2. La Fig. 16.30 muestra el circuito ya mejorado.

                          
Fig. 16.30 – Circuito multivibrador astable mejorado

 

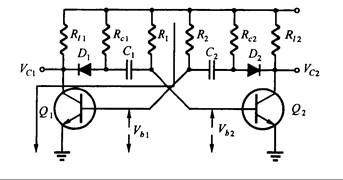
En la Fig. 16.30, cuando C2 está cargando, la corriente no puede fluir a través de RL2 debido a que en el diodo D2 la corriente de carga fluye a través de RC2. Por lo tanto, VC2 puede levantar desde 0 hasta VCC y ya no existiría ninguna esquina redondeada en la onda. La misma razón se puede aplicar a C1 cuando el camino de carga es de D1 y RC1. Para la descarga, el diodo está bajo polarización directa y se tiene solamente una pequeña impedancia. Por ello casi no hay efecto para la constante de tiempo de descarga, y se puede ignorar.

En la Fig. 16.30, para garantizar que el circuito está en resonancia, los transistores en el multivibrador astable deben estar en saturación cuando están bajo conducción. Cuando Q1 está conduciendo, IB1 está siendo alimentado por VCC a través de R2. Para que IB1 empuje a Q1 a la condición de saturación, el análisis es el siguiente:

              

 

---Ver Libro de Texto---

La ganancia del transistor Q2 es:

---Ver Libro de Texto---

Ejemplo 16.8. En el multivibrador astable de la Fig. 16.27, determine el periodo de la señal de salida, la frecuencia y la ganancia mínima del transistor.

Respuesta:

---Ver Libro de Texto---

La ganancia mínima del Q1 y Q2 es:

---Ver Libro de Texto---

 

 

 

 

 

 

•     Multivibradores Monoestables

 

Se llama multivibrador monoestable al multivibrador de un disparo. Está compuesto de un multivibrador estable y de otro transciente. La Fig. 16.31(a) muestra a dos transistores que están conectados en forma de multivibrador monoestable. Cuando se aplica tensión, Q1 adquiere de R polarización de base y conduce. Cuando Q1 está en estado de saturación, VC1  0V no puede obtener la polarización  normal del divisor de tensión R1R2 en el colector VC1 de Q1. Por lo tanto, Q2 está en estado de corte. Cuando VC2 = VCC, el terminal izquierdo del capacitor C es positivo, y el derecho es negativo. Comienza a cargar hasta que VC = VCC – VBE1 = VCC – 0.7V. Cuando el exterior produce una señal de disparo, después del circuito diferencial (CT y RT) combinados, y el diodo corta la onda, se suministra una señal aguda de onda. Esta súbita tensión negativa en la base de Q1 hará que el transistor quede en corte. En este momento, VC1 levanta desde 0 hasta VCC (VC1 = VCC). Una vez que las tensiones de R1 y R2 se han dividido, se obtiene polarización directa en la base de Q2. Esto induce a Q2 al estado de saturación, y la tensión VC2 cae desde VCC hasta 0V (VC2   0V).

 

Como resultado, el capacitor C descargará a través de R y de Q2 CE. El terminal de abajo de R se mantiene con tensión negativa y la base de Q1 con polarización inversa. Por lo tanto, Q1 todavía estará en condición de corte. En este momento, aún cuando  la señal de disparo desaparece, Q1 todavía está en condición de corte. Después de que C ha descargado por un tiempo, la corriente decae y la tensión negativa en el terminal de abajo de R disminuirá, aumentando la tensión negativa en el terminal de abajo de R.  Cuando la tensión negativa se eleva a VB1, Q1 adquiere estado de saturación y Q2 está en corte. Q1 mantiene la saturación y Q2 estará en corte si no se perciben más señales de disparo en la entrada. La Fig. 16.31(b) muestra la forma de la onda para diferentes nodos.
En la Fig. 16.31(a), se tiene un capacitor de 10 pF conectado en paralelo con R1 de 10 kW. Este capacitor es para aumentar la velocidad de aumento y disminución de la salida de la onda de VC1. Con ello también se evita que se formen ángulos redondeados. VC2 induce este tipo de ángulos debido a la carga desde R hasta C.
El tiempo del ciclo T de VC1 es el tiempo de descarga del capacitor C, que fluye a través de Q2, VCC y R. El ancho del cuadrado de la salida es aproximadamente:

T = 0.7 RC                                                                                       (16.22)

Ejemplo 16.9. En el circuito de la Fig. 16.31(a), después de que ha disparado, si deseamos recibir de VC1 una salida con un ancho de 200 mS, ¿Cuál es el valor de R si el capacitor C = 0.1 mF?

Respuesta:  Mediante la Ecuación (16.22),

---Ver Libro de Texto---

 

                                          

(b)  Ondas de nodo de multivibradores monoestables

Fig. 16.31 – Circuitos de multivibradores monoestables y ondas de nodo

 

 

16.3.3    Multivibradores Biestables

Al multivibrador biestable también se le llama “flip-flop”. Tiene dos estados estables. Permanece en estado estable cuando no recibe la señal de disparo, y cambia al otro estado después de recibir la otra señal de disparo. Por ello se le llama biestable, puesto que se puede mantener estable bajo cualquier estado. Solamente cambia de estado después de haber sido disparado. La forma de la onda es cuadrada. En circuitos digitales se usa como memoria o como generador de ondas cuadradas.

 

              

 

Fig. 16.32 – Multivibrador biestable y forma de la onda.

 

La Fig. 16.32(a) muestra los dos transistores conectados en forma de multivibrador biestable. Cuando se aplica la fuente de tensión, uno de los transistores conduce y el otro está en reposo debido a que ambos no tienen características idénticas. Asumiendo que Q1 está en reposo (off) y que VC1 = VCC es la tensión dividida por R2 y R3, entonces la base de Q2 está conectada. Q2 conduce y entra en la región de saturación debido a ganancia de polarización directa. Ahora VC2  0V, VC2 se ve dividido por R1 y R4, y luego se conecta a la base de Q1. Q1 no tienen suficiente polarización, por lo que todavía permanece en estado de corte, y permanece en tal estado, y Q2 en estado de saturación hasta que haya un pulso positivo en la base de Q1. Este pulso positivo hará que Q1 adquiera polarización directa y conduzca. Por lo tanto, VC1  0V, VC1 se divide entre R2 y R3 y luego conectada a la base de Q1, permitiendo que Q2 corte por falta de suficiente polarización. Por lo tanto, ahora se tiene saturación en  Q1 y Q2 está en estado de corte. Q1 y Q2 no cambian de estado hasta que haya un pulso positivo en la base de Q2.

 

En la Fig. 16.32(a) se tienen dos capacitores de 10 pF conectados por separado con R1 y R2 en paralelo. Estos capacitores se usan para aligerar el tiempo de transferencia de los dos transistores. Generalmente, se conectan dos impulsos de disparo en paralelo y se conecta la señal externa de disparo después de haber pasado por el circuito RC diferencial en serie. Q1 y Q2 cambian de estado cuando no hay entrada de señal de disparo. Habrá cambio de estado para cada disparo, por lo tanto el periodo de salida es dos veces el periodo de la señal de disparo, como se muestra en la Fig. 16.32(b).

Ejemplo 16.10. En un multivibrador biestable, si el pulso de disparo continuo tiene un periodo de 100 ms, ¿cuál es el periodo de salida?

Respuesta:  El periodo de salida es dos veces el periodo de disparo de entrada, por lo tanto,

Periodo de salida es: 100 ms x 2 = 200 ms.

 

 

•     Disparador Schmitt

 

El circuito disparador Schmitt también se conoce como “circuito rectificador de onda”. Puede convertir las diversas formas de onda en ondas cuadradas puras, pero no puede generar ondas de oscilación. Sin embargo, se deriva del circuito multivibrador biestable, por lo tanto, la salida es una onda cuadrada pura.
La Fig. 16.33(a) muestra el circuito de un disparador Schmitt, compuesto por dos transistores, con dos diferentes niveles de disparo. Uno se llama nivel alto de disparo  y el otro nivel bajo de disparo (UTL, LTL, respectivamente, en Inglés). Se utilizan para diferentes tipos de funciones. Cuando la fuente de tensión se aplica en Q1, éste estará en corte debido a que no tiene la polarización adecuada. Q2 obtiene la polarización directa de RC1, R y RB2, por lo cual está en conducción. En este momento, IE2 fluye a través de RE e induce una caída de tensión VE2 (VE2 = IE2 x RE). La tensión de salida es Vout = VC2 = VCC – IC2 x RC2, que es Vout = Vce(sat) + IE2 x RE. Cuando la tensión de entrada Vin comienza a elevarse, una vez que adquiere UTL, Vin recibe la tensión del conmutador VB1. Esto es VUTL = VB1 = VBE1 + VE » 0.7V + IE2 x RE, lo que hace que Q1 adquiera la polarización directa y conduzca. Por ello, IC1 aumenta y VC1 decae, siendo VC1 dividido por la tensión en R3 y RB, y luego se induce una caída VB2. Q2 conducirá menos e IE2 decae, igual que VE. La polarización directa de Q1 se aumenta y Q1 conduce más. VC1 decae aún más y Q2 se acerca al estado de corte. Repitiendo esta realimentación positiva, Q1 alcanzará el estado de saturación y Q2 se aproxima al corte. Estos estados permanecen. En este momento, Vout = VC2 =  VCC, y VE = IE1 x RE. Generalmente, el circuito disparador Schmitt se diseña con RC1 > RC2, e induce IC1 < IC2. Por lo tanto IE1 x RE < IE1 x RE. Esto asegura que Q2 pueda ser transferido como estado de corte cuando está en estado de saturación y Vin se

 

aproxima a VUTL. La salida aumenta hasta VCC. Si Vin es más alta que VUTL, y permite que Q2 cambie de estado. Esto hace que comience a declinar, y debe caer hasta menos de VUTL, donde VUTL = VB1 = IE1 x RE. Q1 cambiará a estado de corte, y Q2 recibirá polarización directa de RC1, R y RB2, luego será conducido y regresa a estado de saturación. La tensión de salida se convierte en Vout = VC2 = VCE(sat) + IE2 x RE. La Fig. 16.33(b) muestra la forma de las ondas de entrada / salida.

 

   

(b) Forma de onda del circuito Schmitt

Fig. 16.33 – Circuito disparador Schmitt y forma de las ondas

 

 

 

En diseño general, RC1 > RC2, y por lo tanto IC1 < IC2, IE1 < IE2 , y :

   
Fig. 16.34 – Circuito disparador Schmitt y onda rectificada

 

Si una señal irregular entra al circuito disparador Schmitt, la salida se rectifica con igual amplitud en forma de cuadrados, como se muestra en la Fig. 16.34.

 

•     Osciladores de Bloqueo

Los osciladores de bloqueo constituyen otro tipo de oscilador no senoidal, perteneciendo al grupo de los osciladores libres.  Utiliza el acople de un transformador y se combina con un amplificador a transistores, como lo muestra la Fig. 16.35. El transformador debe tener un coeficiente de acoplamiento de aproximadamente 1, y por lo tanto su núcleo de hierro es de aleación de alto flujo magnético. Debe haber un acoplamiento muy fuerte, y pocas fugas, así como una capacitancia distribuida entre la bobina primaria y secundaria. La bobina secundaria deberá tener más vueltas que la primaria (generalmente NP / NS = 1/3). Como la realimentación positiva es más del 100%, el amplificador está bajo estados periódicos de saturación / conducción y corte. El tiempo de conducción es más corto que el de corte, y el transistor bloquea la conducción. Esta es la razón por la cual se le llama “oscilador de bloqueo”.

 

En la Fig. 16.35, cuando  se aplica tensión al circuito, el transistor Q1 será conducido debido a que recibe polarización directa de R1. IC cambia de bajo a alto. IC inducirá un campo magnético variable cuando pasa por la bobina primaria LP. El campo magnético variable se acoplará a la bobina secundaria LS e inducirá una tensión muy grande de realimentación positiva. El transistor estará súbitamente en estado de saturación e IC ya no se cargará más. El capacitor C1 se carga con la tensión inducida (cerca de 3 veces la tensión de la bobina primaria) de LS. Cuando el IC cesa de cambiar debido a saturación, LP ya no experimentará más cambio en el campo magnético, e IS no tendrá fuerza electromotriz inducida. El capacitor C se descarga a través de R1, LS y VCC. El terminal de abajo de R1 inducirá tensión negativa y dejará que el transistor entre en estado de corte. R1, C1, la constante de tiempo, la polarización del transistor y VCC,  todos determinan el tiempo necesario. Cuando el C1 descarga hasta que la base del transistor gane polarización directa (VBE + VEE), el transistor volverá a conducir de nuevo. Estos procedimientos se repiten una y otra vez.

 

                                    

Fig. 16.35 – Circuito oscilador bloqueador

La Fig. 16.36 muestra la forma de la onda del oscilador bloqueador. En la Fig. 16.36, a y b son los tiempos de conducción durante la oscilación y la tensión inducida en la bobina secundaria LS. En este circuito de realimentación LC, el transformador produce la oscilación libre. El inductor efectivo Le de la bobina secundaria y el capacitor de distribución Co determinan la frecuencia, que es
f = 1 / [2p Ö(LeCo)] . En realidad, el tiempo de conducción es aproximadamente el medio periodo positivo de la señal de oscilación libre, por lo tanto:

            

 

El oscilador de bloqueo se puede usar para un disparador de señal sincrónica, lámparas fluorescentes DC y en el circuito de barrido vertical de TV.

 

                              

Fig. 16.37 – Circuito de lámpara fluorescente

La Fig. 16.37 muestra la aplicación del circuito en una lámpara fluorescente. El transistor tiene cambios alternos ON / OFF debido al capacitor Cb, que carga y descarga. N1 tendrá cambio en la corriente. De acuerdo con el teorema de los transformadores, afectará a N3. Como la relación entre N3 y N1 es de unas 600/20 = 30, la tensión aplicada en la lámpara fluorescente es unas treinta veces la de VCC. La tensión hace que la lámpara brille, y la resistencia variable de 10 kW puede ajustar la intensidad de la luz.

 

 

 

•     Generador de ondas en diente de sierra

 

La Fig. 16.38 muestra una onda típica con forma de diente de sierra. La amplitud comienza con el valor inicial, y aumenta linealmente hasta el valor pico. Luego, regresa a su valor inicial. El tiempo entre el valor inicial y el valor pico se llama tiempo de barrido, denotándose por Ts. El tiempo desde el valor pico al valor inicial se llama tiempo de retorno, y se denota con Tr.

Generalmente la onda de retorno es independiente del tiempo, y en algunas aplicaciones, el tiempo de retorno Tr se requerirá que sea mucho menor que el tiempo de barrido Ts. Cuando Tr »  0, se le considera como una onda ideal en diente de sierra. Se aplican en TV de radares y en probadores.

 

                                    
Fig. 16.38 – Onda de diente de sierra

 

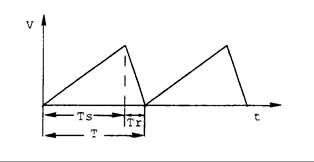
Existen muchos métodos para generar ondas de diente de sierra. Básicamente, se usa el teorema de carga / descarga de un capacitor para producir la onda, como lo muestra la Fig. 16.39(a). Aquí, la resistencia y el capacitor se conectan en serie entre sí, y se deja que el capacitor se cargue lentamente y se descargue rápidamente. Cuando el interruptor S1 se cierra y S2 se abre, la fuente de tensión Vs carga de C a R. Después de 5 veces la constante de tiempo (5T = 5RC), el capacitor estará cargado con un valor cercano a Vs.

Cuando luego  se abre S1 y se cierra S2, el capacitor se descarga súbitamente; la tensión en el capacitor decae hasta 0, y como el capacitor sube su valor en forma exponencial durante el proceso de carga, no se obtiene una elevación lineal, tal como lo muestra la Fig. 16.38(b). Por lo tanto, S2 se cierra en un tiempo de 0.1 RC. La curva tendrá una forma muy cercana a la línea recta (error de menos de un 5%).

 

  

     

Fig. 16.39 – Circuito generador de onda en diente de sierra y forma de la onda mediante capacitor.

Al reemplazar el interruptor por un transistor, como en la Fig. 16.40(a), si no hay señal de entrada el transistor estará en estado de corte. La fuente de tensión Vs carga el capacitor desde RC. Cuando  la señal de entrada es un pulso positivo, el transistor está en estado de saturación. El capacitor se descargará por el transistor hasta llegar a la tensión de saturación del colector VCES. Para lograr la forma de onda de salida lineal, el periodo de la señal de entrada debe ser menor de 0.1 RC, como se ve en la Fig. 16.40(b).

            

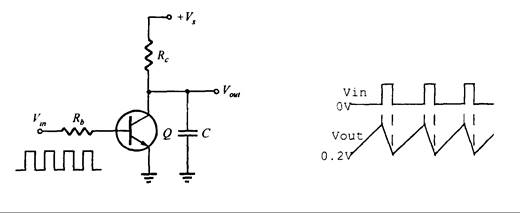
    (a) Circuito                                                   (b) Onda en funcionamiento

 

Fig. 16.40 - Circuito generador de onda en diente de sierra y forma de la onda mediante transistor

En aplicaciones prácticas, se puede usar un multivibrador astable o un oscilador bloqueador para generar la señal de entrada, como se muestra en la Fig. 16.40(a). En la Fig. 16.41, en el circuito hay un multivibrador astable y un generador de diente de sierra.

 
Fig. 16.41 – Generador de ondas de diente de sierra.

 

 

•     Generadores de ondas triangulares

En la Fig. 16.42 se muestra una onda triangular. En esta forma de onda se encuentran ondas de pendiente superior y ondas de pendiente inferior. Básicamente, si se controla el circuito de carga / descarga, se puede obtener una corriente igual de carga / descarga para lograr un generador estándar de ondas triangulares.

 

                        

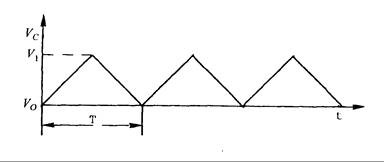
Fig. 16.42 – Ondas triangulares

La Fig. 16.43 es un circuito capacitor típico que genera ondas triangulares. Se tienen dos fuentes constantes de corriente, i1 e i2, también i1 = i2. Cuando S1 se cierra y S2 se abre, C se carga por la corriente constante y VC = V1 después de un tiempo t1. Luego, se abre S1 y se cierra S2, y C se descarga por la corriente constante y VC = V0 después de un tiempo t2. Luego S1 se cierra y S2 se abre, repitiéndose este proceso y produciéndose una salida de ondas triangulares simétricas.

 

         

• Resumen

 

      1. Realimentación significa separar parte o toda la señal de entrada del circuito de amplificación para el terminal de entrada del circuito, y usarla luego como señal de control de salida.

2.  La ganancia de tensión para un circuito de amplificación con circuito de realimentación es Af = A / (1 - bA), A es la ganancia de tensión antes de la realimentación, y b es la realimentación.

1. En un circuito de realimentación, cuando bA es negativo, se llama realimentación negativa. Hará que Af < A, y disminuye la ganancia total del circuito.

 

2. En un circuito realimentado, cuando bA es positivo, se le llama realimentación positiva. Si 1-bA es menor que 1, entonces la ganancia del circuito amplificador se aumenta.

3. Cuando bA = 1, la ganancia del amplificador se hace infinita. Por lo tanto, no importa el tipo de fuente, se amplifica y se induce la oscilación.

 

4. Para inducir la oscilación, bA debe ser igual a 1, y a esto se le llama criterio de Barkhausen.

5. Hay dos criterios para el diseño de osciladores: (1) realimentación positiva, (2) satisfacer el criterio de Barkhausen, de bA = 1.

 

6. Un oscilador senoidal de baja frecuencia generalmente usa una resistencia (R) – capacitor (C) para inducir la oscilación. El oscilador senoidal de alta frecuencia usa un inductor (L) – capacitor (C) para lograr una realimentación positiva.

7. El oscilador de cambio de fase usa una red capacitor – resistencia para producir la variación de fase y lograr realimentación positiva.

 

8. Una red de cambio de fase con resistencia – capacitor tiene dos variantes, una es de adelanto y la otra de retraso.

9. Una red RC de cambio de fase de tres etapas puede producir un cambio de 60º en cada etapa. La ganancia de amplificación debe ser mayor de 29.

 

10. La frecuencia de un oscilador de cambio de fase de tres etapas es f0 = 1/ (2pRC Ö6).

11. El oscilador puente Wien usa un circuito puente  de adelanto – retraso como realimentación.

 

12. La frecuencia de oscilación del oscilador puente Wien es f0 = 1/ (2pRC ).
13. El oscilador doble T usa filtros de doble T como red de realimentación

14. La frecuencia de  oscilación del oscilador doble T es f0 = 1/ (2pRC ).

 

15. El oscilador Colpitts usa un oscilador LC, y el capacitor divisor de tensión funciona como circuito de realimentación, donde b = C1/C2.
16. La frecuencia de oscilación de Colpitts es f0 = 1/ (2pÖRC).
17. La ganancia mínima de tensión AV del circuito de amplificación  con oscilador Colpitts debe ser mayor o igual a C2 / C1.
18. El oscilador Hartley es un oscilador LC de alta frecuencia, y el inductor del divisor de tensión es el circuito de realimentación, donde b = L2 / L1.
19. La frecuencia de oscilación del oscilador Hartley es f0 = 1/ (2pÖLC).
20. La ganancia mínima de tensión AV del circuito de amplificación  con oscilador Hartley debe ser mayor o igual a L1 / L2.
21. Un oscilador Clapp se mejora con un oscilador Hartley. Para evitar el efecto dispersivo del capacitor en el capacitor de resonancia, hay un pequeño capacitor (CS) conectado en serie con el inductor.
22. La frecuencia de oscilación de un oscilador Clapp es f0 = 1/ (2pÖLCS).
23. El oscilador de cristal tiene una frecuencia de operación de alta estabilidad, la variación de frecuencia es menor a 10-6 cada día. Es muy adecuado como referencia de tiempo.
24. Para diferentes ángulos de corte y diferentes métodos, se obtienen diferentes características piezoeléctricas. El espesor del cristal determina la frecuencia fundamental de oscilación.
25. Para un cristal se tienen dos frecuencias de resonancia: frecuencia resonante serie, y frecuencia resonante paralela.
26. Las salidas de un multivibrador no solamente tienen ondas senoidales básicas, sino que también frecuencias multi – resonantes. Se combinan las dos en forma de ondas cuadradas.
27. A un multivibrador astable también se le llama multivibrador de corrida libre. Ofrece una serie de salidas de pulsos pero no requiere una señal externa de disparo. Su periodo de salida es T » 0.7 R2C2 + R1C1) » 1.4 RC.
28. A un multivibrador monoestable también se le llama multivibrador de un solo disparo. Se compone de un multivibrador estable y de otro transciente. El disparo de entrada produce una salida de onda cuadrada, cuyo periodo es aproximadamente T = 0.7 RC.
29. Al multivibrador biestable se le llama también flip-flop. Tiene dos estados estables, por lo que en todo momento está en estado estable. Solamente cambiará a otro estado cuando hay una entrada de señal de disparo. El multivibrador  biestable se puede usar en memorias o como generador de ondas cuadradas.
30. Al disparador Schmitt también se le llama circuito rectificador de onda. Puede convertir las diferentes ondas irregulares en ondas cuadradas puras.
31. Un oscilador de bloqueo es un oscilador libre. Se compone de un acople de transformador y de un amplificador con transistor sencillo. Su realimentación es mayor del 100%. El periodo del amplificador  se compone de los estados de saturación / conducción y de corte. El tiempo de conducción es más corto, y el de corte es más largo. El transistor es conductivo temporalmente.
32. El generador de ondas en diente de sierra usa el teorema de carga / descarga de un capacitor. Generalmente usa un circuito serie de resistencia – capacitor. El capacitor se carga lentamente y se descarga en forma rápida. Para mejorar la característica lineal, el tiempo de cambio es de solamente 0.1 RC.
33. El generador de ondas triangulares usa el mismo teorema que el generador de ondas de diente de sierra. Su principal característica es controlar la corriente constante de carga / descarga.

 

• Preguntas

1. La principal aplicación de la realimentación positiva es ______, que puede producir una salida con frecuencia constante aún cuando no haya señal de entrada.
2. La condición necesaria para completar la oscilación se llama ______.
3. En ciertas frecuencias, el cambio de fase del bucle es de 0º. Si la ganancia de bucle bA es mayor que 1, entonces puede comenzar a oscilar. Cuando la señal de salida ha alcanzado el nivel deseado de amplitud, la ganancia de bucle debe ser igual a ______, y luego la señal de oscilación será estable.
4. Para un oscilador variador de fase, la variación de fase del amplificador es de 180º. En cierta frecuencia, una red de tres etapas puede producir una variación de fase de 180º, también. Como resultado, la variación de fase del bucle es igual a ______º. El circuito de realimentación del oscilador variador de fase puede usar también las tres etapas de la red ______.
5. Si se usa un circuito RC para producir la variación de fase de 180º, se necesitan por lo menos ______ circuitos RC.
6. En un oscilador variador de fase de tres etapas, la frecuencia de oscilación fo = ______. La ganancia necesaria AV requiere al menos ______.
7. El oscilador puente Wien usa la estructura de equilibrio del puente para lograr la frecuencia de equilibrio de la realimentación positiva / negativa como frecuencia de oscilación fo. Si en el puente, la resistencia es R y la capacitancia C, entonces f0 = ______. La ganancia de tensión del circuito amplificador en el oscilador Wien es de aproximadamente ______.
8. El oscilador puente Wien usa ______ como red de realimentación.
9. El oscilador de puente Wien es el oscilador más popular. Su frecuencia de oscilación es de 5 Hz a 1 MHz. El puente Wien tiene una red de adelanto y otra de atraso. A ciertas frecuencias, la variación de fase de la red es igual a 0º. Esta frecuencia es la frecuencia ______ de la red de compensación de adelanto / atraso.
10. El oscilador común en un generador de señales de baja frecuencia es ______.
11. ______, ______ y ______ usan osciladores RC senoidales.
12. La frecuencia de oscilación del circuito oscilador LC es de ______. (si Q > 10), la capacitancia equivalente del oscilador Colpitts es ______.
13. En un oscilador Colpitts, se usa ______ como realimentación positiva.
14. Generalmente, el circuito de realimentación en el oscilador Hartley está compuesto de ______.
15. El punto de tierra de un oscilador Hartley se encuentra entre los dos inductores. En el oscilador Colpitts, se encuentra entre los dos ______. La frecuencia de oscilación del oscilador Clapp es más ______ que la del Colpitts. Sin embargo, el oscilador de cristal tiene todavía una mejor estabilidad de frecuencia de oscilación.
16. Generalmente existen ______, ______, y ______ para el oscilador RF.
17. Cuando el cristal vibra por señales eléctricas, se asemeja a un circuito de modulación. El cristal tiene un circuito equivalente con mejor modulación que el circuito LC resonante normal. La principal característica es ______,  que puede ser tan alta como 10,000.
18. Para mantener la frecuencia de oscilación estable, es preferible usar ___.
19. Los multivibradores se pueden dividir en tres tipos: ______, ______, y ______ .
20. Un multivibrador usa dos transistores como amplificador de emisor común. Cuando se usan capacitores como dispositivo de realimentación, generalmente es un multivibrador ______ . Si se usa una resistencia como dispositivo de realimentación, generalmente se trata de un multivibrador ______. Si hay una resistencia y un capacitor como dispositivo de realimentación, es un multivibrador ______.
21. Generalmente, en un multivibrador se tiene un capacitor de 10 pF en paralelo con la resistencia. A esto se le llama ______. El propósito es mejorar el cambio de estatus.
22. Un multivibrador astable no requiere una señal externa de disparo. Puede producir la oscilación por sí mismo. La salida es ______. Por ello se le llama multivibrador libre.
23. Cuando R1 = R2 = R, C1 = C2 = C, el periodo T del pulso de salida de un multivibrador astable es de ______, y la frecuencia es ______.
24. La oscilación y el ancho de pulso de un oscilador astable se puede cambiar por una realimentación positiva producida por una resistencia y ______.
25. Un multivibrador ______ ofrece una serie de salidas de pulsos, pero no requiere una señal externa de disparo.
26. Un multivibrador monoestable puede generar una salida de pulso por cada disparo. El circuito tiene un ______, y un ______, por lo que se le llama multivibrador de un disparo.
27. El multivibrador monoestable generalmente se usa como circuito ______, ______, y ______.
28. Un multivibrador biestable tiene dos estados estables, y su principal función es como circuito ______. En circuitos digitales lógicos, es el circuito básico ______.
29. La suma de una onda senoidal básica y una onda harmónica impar es ______.
30. El disparador ______ se usa para producir la salida de un circuito digital.
31. Los dos transistores de un circuito disparador Schmitt usan una resistencia ______, que puede usarse para determinar la intensidad de la señal de entrada.
32. Un circuito Schmitt tiene ______ aplicaciones. Si se tiene una entrada senoidal, la salida es siempre una onda ______ en el nivel de disparo entre alto y bajo.
33. El circuito disparador Schmitt es un circuito ______. Puede convertir lentamente la señal AC en una salida de pulsos agudos altos y bajos.
34. Un oscilador de bloqueo usa ______ para generar realimentación positiva.
35.Un oscilador bloqueador generalmente se usa en ______.

34. Una lámpara fluorescente  generalmente usa un oscilador ______.
35.  El generador de ondas de diente de sierra tiene solamente una _____  (descendiente), y cuando la pendiente se levanta (o cae) hasta cierto punto, ______ a su punto más bajo.
36. En la onda triangular hay dos partes principales: ______, y ______.
37. Los osciladores no senoidales incluyen ______, ______, y ______.

 

• Problemas

1. ¿Qué es realimentación?
2. ¿Qué es el criterio de Barkhausen?
3. Describa la definición de un oscilador.
4. ¿Cuáles son las condiciones necesarias para generar y conservar una oscilación?
5. En un amplificador, su realimentación positiva b = 0.02. ¿Cuál es AV para la oscilación?

6. ¿Cuáles son en la práctica los dos tipos de oscilador senoidal positiva ¿

7. En su red de adelanto de tres etapas, un oscilador variador de una fase R y C son 500 kW y 50 pF. ¿Cuál es la frecuencia de oscilación?

8. En un circuito resonante, se conecta en serie un inductor de 30 mH con capacitores en paralelo de 200 y 300 pF. ¿Cuál es la frecuencia resonante?

9. El capacitor en un oscilador Hartley se puede ajustar entre 100 y 400 pF, y la bobina de oscilación tiene L = 900 mH. ¿Cuál es el rango de frecuencia de oscilación?

10. ¿Qué es el efecto piezoeléctrico?

11. En un cristal de cuarzo,  su frecuencia fundamental de resonancia   paralela es de 5 MHz. ¿Cuál es la primera frecuencia alta de resonancia? ¿La segunda?, ¿La tercera?

12. En un cristal de cuarzo, la resistencia AC equivalente es como sigue: L = 1 H, CS = 0.01 pF, R = 1000W, y Cm = 20 pF.

• ¿cuál es la frecuencia resonante serie?
• ¿Cuál es la frecuencia resonante paralela?

 
13. En una lámina delgada de cristal, k = 112.6 kHz/pulgada. Si t = 0.1 pulgada, ¿cuál es la frecuencia resonante? ¿cuál es la frecuencia resonante si t = 0.005 pulgada?

14. Dibuje y describa el teorema de operación de un multivibrador astable y la forma de la onda de cada colector y basa.

15. En el multivibrador astable de la Fig. 16.27, si el circuito es totalmente simétrico, Q1 = Q2, C1 = C2 = 0.1 mf, R1 = R2 = 100 kW, RC1 = RC2 = 5 kW, ¿cuál es la frecuencia de oscilación?

16. Dibuje y describa el teorema de operación de un multivibrador monoestable.

17. Compare el circuito y las diferencias en funcionamiento de los tres multivibradores.

18.Dibuje y describa el teorema de operación de un disparador Schmitt.

19. Dibuje y describa el teorema de operación de un oscilador de bloqueo

20. ¿Cuál es la diferencia entre un generador de ondas triangulares y uno de ondas en diente  de sierra?

21. Describa las características del circuito de un oscilador de bloqueo.

22. ¿Qué es un capacitor acelerador? ¿Cuál es su función?