Los resúmenes, toma nota de los textos que figuran en nuestra página web se ponen a disposición de forma gratuita con fines didácticos de la ilustración, científica, social, civil y cultural a todos los posibles interesados de acuerdo con el concepto de uso justo, y con el 'objetivo de cumplimiento de la Directiva Europea 2001/29 / CE y del «arte. 70 de la ley 633/1941 sobre derechos de autor
La información médica y de la salud en este sitio es de carácter general y para propósitos informativos solamente y por lo tanto no puede en ningún caso sustituir el consejo de un médico (o un autorizado legalmente a la profesión).
En el presente capítulo discutiremos el circuito resonante. De manera especial se presentarán las combinaciones y características del mismo, por lo cual, en la Sección 10.1 se ve el circuito resonante combinado con dispositivos L-C básicos y sus características. En la Sección 10.2, Circuitos Resonantes RLC en Serie, y en la Sección 10.3 Circuitos Resonantes RLC en paralelo, le suministran a los estudiantes las características del circuito resonante RLC.
Finalmente, en la Sección 10.4, se discute la utilidad del circuito resonante, y en la Sección 10.5, se presentan las aplicaciones de los mismos. Es de esperar que el estudiante aprenda los principios del circuito resonante, la relación entre los parámetros, y los campos de aplicación práctica.
En esta sección presentamos el circuito resonante L-C, y se divide en dos partes: 10.1.1, Circuitos Resonantes LC en Serie y 10.1.2, Circuitos Resonantes es Paralelo.
Para comenzar, revisemos las características de los capacitores e inductores, vistos en los primeros capítulos y podemos clasificar las relaciones entre dispositivos con impedancia y frecuencia como:
La Fig. 10.1 muestra las relaciones entre reactancia inductiva, reactancia capacitiva y frecuencia. Se pueden dividir como tres condiciones que:
La Fig. 10.1(a) muestra las relaciones entre reactancia inductiva y frecuencia. XL = 2p f L, donde 2 pL es constante, por lo que la reactancia inductiva es proporcional a f, con una relación lineal.
La Fig. 10.1(b) muestra la relación entre reactancia capacitiva y frecuencia. XC = 1/ (2 p f C), donde 2pC es constante, por lo tanto la reactancia capacitiva es inversamente proporcional a f con una relación curva.
(a) Reactancia Inductiva vs Reactancia capacitiva vs
frecuencia frecuencia
Fig. 10.1 Relaciones

Cuando se conecta un inductor L y un capacitor C en serie, como se muestra en la Fig. 10.2(a), se tiene:
Reactancia inductiva, así como también,
que es la reactancia capacitiva y la impedancia total. Al aplicar una fuente de frecuencia ajustable en el circuito en serie, se obtiene la curva de impedancia como se muestra en la Fig. 10.2(b). El eje real es la frecuencia, y el eje imaginario es la impedancia..
Eje imaginario
Frecuencia
f variable
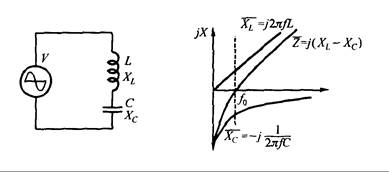
Fig. 10.2 – Circuito LC en serie y curva de impedancia.
En la Fig. 10.2(b), se pueden ver las relaciones entre la impedancia total Z del circuito LC en serie y la frecuencia f :
De lo anterior es posible obtener la curva de respuesta de la corriente vs frecuencia, como se muestra en la Fig. 10.3. En este diagrama, cuando la frecuencia fuente = f0, la corriente es muy alta. Se le llama resonancia LC en serie. Esto sucede cuando XC = XL, es decir:
Fig. 10.3 – Curva de respuesta para corriente vs. frecuencia en
un circuito LC en serie
Inductivo
Capacitivo

f0 es la frecuencia resonante, que también se expresa como fr. Cuando la frecuencia externa es igual a f0, hará que la impedancia del circuito = 0. Este circuito se llama “circuito resonante” y la frecuencia externa se llama “frecuencia resonante”. En la Fig. 10.3, cuando la frecuencia externa f es menor que f0, XL < | XC|, el circuito es capacitivo, y la corriente va adelantada 90º con respecto al potencial. Cuando la frecuencia externa f es mayor que f0, entonces XL > | XC|, el circuito es inductivo, y la corriente va atrasada 90º con respecto al potencial.
Ejemplo10.1. L = 0.4 H, C =100mf en serie. Determinar la frecuencia resonante.
Respuesta: De acuerdo con la Ecuación (10.1),
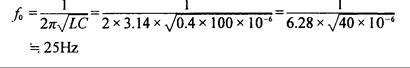
Al conectar un capacitor y un inductor en paralelo, como se muestra en la Fig. 10.4(a), se obtienen respectivamente la suceptancia del conductor, la admitancia total y la suceptancia del inductor con las siguientes fórmulas:
(a) circuito L-C paralelo (b) Curva de respuesta BL, BC, e Y
vs. frecuencia

Fig. 10.4 – Circuito paralelo L-C y curva de respuesta
De la Fig. 10.4(b) obtenemos la relación entre frecuencia y admitancia total del circuito LC en paralelo como sigue:
De lo anterior es posible obtener la curva de respuesta de la corriente vs frecuencia, como se muestra en la Fig. 10.5. En este diagrama, cuando la frecuencia fuente = f0, la corriente es cero. Se le llama resonancia LC en paralelo. Esto sucede cuando BC = BL, es decir:
siendo la frecuencia de resonancia

Cuando está en resonancia:
Fig. 10.5 – Curva de respuesta de la Corriente vs. Frecuencia en un circuito LC en paralelo
Ejemplo 10.2: L = 1 H, C =100mf en paralelo, con una fuente de tensión de 100 V con frecuencia variable. Determinar (1) la corriente resonante, y (2) la corriente a través del inductor con esa resonancia.
Respuesta: (1) cuando su resonancia Y = 0, la fuente de corriente I = V x Y = V x 0 = 0A. (2) De acuerdo con la Ecuación (10.2), la frecuencia resonante es:
Ind.
Cap.
En aplicaciones prácticas, no existe un circuito con “inductor puro”, y debe haber una pequeña porción de resistencia interna en el inductor. Por lo tanto, en análisis de circuitos, debemos usar como norma el circuito resonante RLC. En esta sección, presentaremos las combinaciones y características de los circuitos RLC resonantes en serie. En la sección 10.2.1 discutiremos primero la impedancia y el ángulo de fase de los circuitos RLC resonantes en serie. En la sección 10.2.2 se hablará de la potencia y del ancho de banda del los circuitos RLC resonantes en serie, y finalmente en la sección 10.2.3 se discutirá el factor de calidad Q y la selectividad.
La Fig. 10.6 muestra un circuito normal RLC en serie, que se puede considerar como la suma de las resistencias en toda la red en serie, incluyendo la resistencia interna de la fuente de tensión, la resistencia interna del inductor, la resistencia de los alambres o de la resistencia. El capacitor y el inductor se pueden simplificar como dispositivos ideales (con solamente reactancia inductiva y capacitiva, sin ningún otro componente de resistencia).
Finalmente, obtenemos la frecuencia de resonancia del circuito en serie f0 como:
(a) Circuito (b) Diagrama de Impedancia vs.
Frecuencia
Fig. 10.6 – circuito R-L-C en serie
De la Fig. 10.6 sabemos que la impedancia total del circuito es ZT = R+jXL-jXC = R + j(XL-XC). Para producir resonancia en el circuito, la parte imaginaria de la impedancia = 0: XL – XC = 0, o sea XL = XC
Impedancia total ZT
Impedancia
f varia-ble
De la Ecuación (10.3), para el circuito resonante R-L-C en serie, tanto f como L y C deben satisfacer la Ecuación, independientemente del valor de R.
En el circuito de la Fig. 10.6(a), la impedancia total del circuito en serie R-L-C es una curva como se muestra en la Fig. 10.6(b),
---Ver Libro de Texto---
La magnitud y ángulo de la impedancia ZT es:
---Ver Libro de Texto--- (10.4)
---Ver Libro de Texto--- (10.5)
Con resonancia XL = XC, la impedancia de resonancia Z0 = R y q = tan-1 0 = 0º; cuando la frecuencia externa se cambia, el resultado se muestra en la Fig. 10.7:
---Ver Libro de Texto---
---Ver Libro de Texto---
---Ver Libro de Texto---
Fig. 10.7 – Diagramas de impedancia
Si en el circuito no hay resistencia, cuando f > f0 el circuito es inductivo, y el ángulo de fase de la impedancia es +90º. Cuando f < f0, entonces el circuito es capacitivo y el ángulo de fase es –90º. Cuando el circuito es resonante, varía entre inductivo y capacitivo y el ángulo de fase varía entre +90º y –90º. La Fig. 10.8(a) muestra el diagrama de frecuencia y del ángulo de fase de la impedancia. Si consideramos el efecto de la resistencia, el ángulo de fase de la impedancia depende de la resistencia y de la reactancia.
llega a ser muy grande, el ángulo de fase tenderá a +90º o
Cuando
a – 90º, y cuando está en resonancia, el ángulo de fase del circuito es todavía igual a 0º, como se ve en la Fig. 10.8(b).
Angulo de fase q
Angulo de fase q
(a) Sin resistencia (b) con resistencia
Fig. 10.8 – Angulo de fase vs. frecuencia
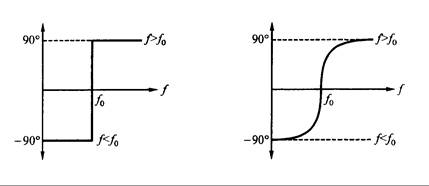
Con una misma frecuencia, cuando R llega a ser más grande, menor será q y viceversa, cuando R se hace más pequeña, q se hará más grande. En el punto de resonancia, el ángulo de fase es todavía de 0 grados. La Fig. 10.9 muestra el diagrama relativo del ángulo de fase y la frecuencia, para diferentes valores de R.
R pequeño R mediano R grande
Angulo de fase q

Fig. 10.9 – Diagrama de ángulo de fase de impedancia vs. Frecuencia para diferentes valores de R.
Ejemplo 10.3. En la Fig. 10.6, R = 10 W, L = 2 mH, C = 2 mF. Determine (1) la frecuencia resonante f0, (2) la impedancia en el punto de resonancia, (3) la impedancia a 60 Hz, la impedancia a 100 Hz.
Respuesta:
(4)
(3)
(2)

De acuerdo con la Ley de Ohm, sabemos que la corriente en un circuito es I = V/Z. En la Fig. 10.6(b), se obtiene la impedancia mínima y la corriente máxima cuando f = f0. Cuando f < f0 o cuando f > f0, la impedancia aumentará cuando la frecuencia se aleja lo suficiente de f0. Cuando f = 0, el capacitor actúa como un circuito abierto, por lo tanto la corriente es cero. Cuando f ® ¥ , el inductor actúa como un circuito abierto, y la corriente se aproxima a cero. Por lo tanto, la curva de respuesta es como la que se muestra en la Fig. 10.10.
La corriente tiene su máxima resonancia. De igual manera, la potencia es máxima en esa resonancia, y por lo tanto, la potencia máxima P0 para el circuito resonante en serie es:
Fig. 10.10 – Curva de frecuencia vs. Corriente
La potencia total inducida por la corriente en cualquier frecuencia es:
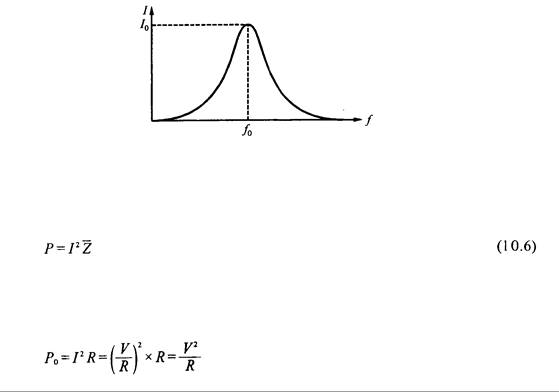
La Fig. 10.11 muestra la curva de frecuencia vs. potencia. En el punto en el que f = f0, es donde habrá la mayor potencia. Cuando f < f0 o cuando f > f0, la potencia se disminuye conforme la frecuencia se aleja de f0.
En la práctica, es difícil que un circuito permanezca en estado de resonancia. Por lo tanto, en general lo que se define es un rango razonable de frecuencia, donde la respuesta de frecuencia es aceptable. Esta respuesta pierde su calidad una vez fuera del rango. A este rango se le llama “Ancho de Banda”.
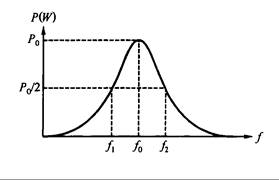
Por lo general, el ancho de banda (BW, por sus siglas en Inglés) se define como el rango entre f2 – f1 de la Fig. 10.11.
BW = Df = f2 – f1 (10.7)
Ambas frecuencias son las cuales la potencia está afectada por un factor de ½ de su máximo, por lo que las frecuencias f2 y f1 se llaman frecuencias de media potencia o frecuencias de corte, dado que la potencia es la mitad de la potencia de resonancia. La razón por la cual se les llama frecuencias de corte es por la respuesta que llega a ser muy pobre cuando f < f1 o cuando f > f2. para lograr una buena respuesta, la frecuencia debe estar entre f2 y f1, es decir, f1 < f< f2. Cuando f = f0, la respuesta de la resonancia es la óptima.
A la mitad de la potencia de la frecuencia , la potencia PHP es:
Cuando la corriente va desde alta hacia baja, la Ley de Ohm nos dice que la impedancia será de baja hacia alta, por lo tanto, la impedancia Z a la mitad de la potencia es:
De la Ecuación (10.8) sabemos que:
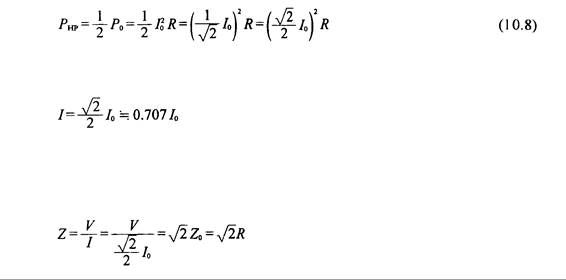
La Fig. 10.12(a) muestra la curva de corriente vs. frecuencia. La Fig. 10.12(b) muestra la curva de impedancia vs. frecuencia.
frecuencia frecuencia
Fig. 10.12 – Curvas de corriente e impedancia para media potencia.
Ejemplo 10.4. Se tiene un circuito resonante en serie con V = 10Ð0º, R = 10 W, L = 1 mH y C = 20 pF. Determine: (1) frecuencia de resonancia, (2) corriente para la resonancia, y (3) la corriente en la frecuencia de corte.
Respuesta:

El factor de calidad Q se define como: la relación entre la potencia de reactancia y la potencia real del inductor o del capacitor, cuando el circuito está en resonancia. Es decir,
En el circuito resonante en serie, las corrientes a través de cada dispositivo son las mismas. Por lo tanto, la disipación de potencia en cada uno será:

---Ver Libro de Texto---
Donde I0 es la corriente en el punto de resonancia, por lo tanto:
---Ver Libro de Texto---
Multiplicando estas dos ecuaciones se obtiene:
---Ver Libro de Texto--- (10.10)
De la Ecuación (10.10) sabemos que entre menos resistencia haya, el valor de Q será más alto. Por lo tanto, para obtener un Q alto, la resistencia se debe mantener a un mínimo. Podemos también elevar la relación entre la inductancia y la capacitancia y obtener un Q más alto.
En el punto de resonancia, I0 = V/R, y el potencial en el inductor VLO y en el capacitor VCO son como sigue:
---Ver Libro de Texto---
---Ver Libro de Texto---
De las dos ecuaciones anteriores sabemos que el potencial en el inductor y en el capacitor tienen la misma magnitud pero un fasor opuesto. Ambos son Q veces el valor de la tensión de la fuente. Por lo tanto es necesario ponerle atención a la tolerancia al potencial del inductor y del capacitor cuando se diseña un circuito resonante en serie con un valor Q alto.
Las potencias a diferentes frecuencias son como sigue:
P = I2 Z, cuando está en frecuencia de resonancia, P0 es máximo y Z=R
---Ver Libro de Texto---
En la potencia media, PHP :
---Ver Libro de Texto---
Las frecuencias son f1 o f2, y la ecuación para la impedancia (10.4) es:
---Ver Libro de Texto---
Por lo tanto, la potencia media es:
---Ver Libro de Texto---
Cuando f1 es la frecuencia de media potencia y f1<f0, w2LC debe tener un valor negativo. Al resolver la siguiente ecuación:
---Ver Libro de Texto---
o sea, ---Ver Libro de Texto---
Usando la misma ecuación para probar que cuando f2 es la frecuencia de media potencia y f2> f0, w2LC debe asumir un valor positivo. Se obtiene que:
---Ver Libro de Texto---
El ancho de banda es:
Fig. 10.13 – Relación entre Q y el Ancho de Banda.
De la Ecuación (10.11) sabemos que el BW es inversamente proporcional a Q. Si la frecuencia de resonancia permanece constante, Q1 > Q2 implica que BW1 es más angosto que BW2, como lo muestra la Fig. 10.13.
De la ecuación anterior sabemos que:

Entre más ancho sea el ancho de banda, peor será la selectividad. Si el ancho de banda es más angosto, se mejora la selectividad. Por lo tanto, la curva en la Fig. 10.13 se llama curva de selectividad. La calidad de la selectividad afectará el efecto de la frecuencia de amplificación. Para una mejor selectividad, el ancho de banda es más angosto, pero se empeora la sensitividad. Por ello, el q más alto producirá un ancho de banda más angosto y hace que la frecuencia no se quede dentro del ancho de banda.
L y C constantes R constante
Fig. 10.14 – Relación entre dispositivo y selectividad

Q se verá afectado por el RLC. Cuando L y C permanecen constantes, entre mayor sea R, se tendrá un Q más bajo. Por lo tanto, el ancho de banda será más amplio, como lo muestra la Fig. 10.14(a). Cuando R3 > R2 > R1, entonces también Q1 > Q2 > Q3. Cuando R se mantiene constante, la relación L / C se hace más alta, el Q se hace más pequeño y el ancho de banda será más amplio, como lo muestra la Fig. 10.14(b).
Ejemplo 10.5. Se tiene un circuito RLC en serie, donde R = 10 W, L = 2 mH, C = 20 mF. Determine: (1) la frecuencia f0 de resonancia, (2) el valor de Q, y (3) el ancho de banda.
Respuesta:

En esta sección se presentarán las combinaciones y características del circuito RLC resonante en paralelo. Primero, discutiremos la impedancia y el ángulo de fase de un circuito RLC resonante en paralelo en la sección 10.3.1. Luego, en la sección 10.3.2 veremos la potencia y el ancho de banda de un circuito RLC resonante en paralelo, y finalmente veremos el factor de calidad Q y la selectividad en la Sección 10.3.3
10.3.1 Impedancia y Angulo de Fase de Circuito RLC Resonante en Paralelo
La Fig. 10.15(a) muestra un circuito normal RLC en paralelo. Para una mayor conveniencia al analizar sus parámetros, se usa la admitancia del circuito. La admitancia total para el circuito es Y = G + j (BC – BL), donde G = 1/R, BC = 1 / XC, BL = 1 / XL. La Fig. 10.15(b) muestra la relación entre admitancia y frecuencia.
(a) Circuito R-L-C en paralelo (b) Curva admitancia vs. frecuencia
Fig. 10.15 – Circuito R-L-C paralelo
La condición para resonancia en el circuito es que la parte imaginaria de la admitancia total sea igual a 0, o sea, BC – BL = 0, lo cual implica que:

Cuando se cambia la frecuencia externa, el diagrama de admitancia es tal como se muestra en la Fig. 10.16:
1. Si f > f0, BL < BC, el circuito es capacitivo. La admitancia aumenta gradualmente y el ángulo de fase de la admitancia será mayor de 0º, como se muestra en la Fig. 10.16(a), es decir,
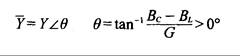

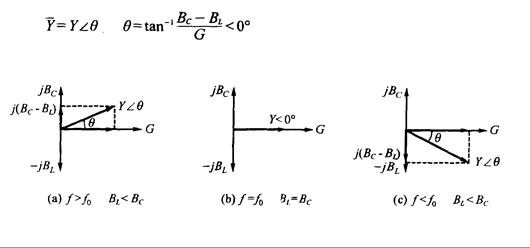
Fig. 10.16 – Diagrama de admitancia para circuito resonante en paralelo.
Si en el circuito no hay resistencia, cuando f > f0 el circuito es capacitivo, y el ángulo de fase de la impedancia es + 90º. Cuando f < f0, entonces el circuito es inductivo y el ángulo de fase es –90º. Cuando el circuito es resonante, varía entre inductivo y capacitivo y el ángulo de fase varía entre +90º y –90º. La Fig. 10.17(a) muestra el diagrama de frecuencia y del ángulo de fase de la admitancia. Si consideramos el efecto de la resistencia, el ángulo de fase de la admitancia depende de la resistencia y de la reactancia.
se hace muy grande, el ángulo de fase se aproxima a + 90º o a – 90º. Cuando entra en resonancia, el ángulo de fase del circuito es todavía igual a 0º, como se muestra en la Fig. 10.17(b).
Cuando el valor
Bajo una misma frecuencia, cuando G se hace más grande, la frecuencia de admitancia q se hará más pequeña, y viceversa, cuando G disminuye, q se hará más grande. En el punto de resonancia, el ángulo de fase es siempre 0 grados, como lo muestra la Fig. 10.18.
Angulo de Admitancia q Angulo de admitancia q
Fig. 10.18 – Relación entre R y la Frecuencia
(a) Sin resistencia (b) con resistencia
Fig. 10.17 – Diagrama de frecuencia vs. ángulo de admitancia
Angulo de admitancia
Ejemplo 10.6. En la Fig. 10.15 se tiene un circuito RLC paralelo, donde R = 10 kW, L = 1 mH, C = 400 pF. Determine: (1) la frecuencia f0 de resonancia, (2) la impedancia en el punto de resonancia, (3) la impedancia a la frecuencia de la fuente de 100 kHz, (4) la impedancia a la frecuencia de la fuente de 400 kHz.
Respuesta: (1) ---Ver Libro de Texto---
---Ver Libro de Texto---
---Ver Libro de Texto---
---Ver Libro de Texto---
De acuerdo con la Ley de Ohm, sabemos que la corriente en un circuito es I = V/Z, y sustituyéndola en Y = I / Z obtenemos que I = VY. En la Fig. 10.15(b), se obtiene la admitancia mínima y la corriente máxima cuando f = f0. Cuando f < f0 o cuando f > f0, la admitancia aumentará cuando la frecuencia se aleja lo suficiente de f0. Cuando f = 0, el capacitor actúa como un circuito abierto, por lo tanto la corriente es cero. Cuando f ® ¥ , el inductor actúa como un circuito abierto, y la corriente se aproxima a infinito. Por lo tanto, la curva de respuesta de la corriente es como la que se muestra en la Fig. 10.19.
Fig. 10.19. Curva de frecuencia vs. corriente en circuito R-L-C paralelo
De la Ecuación (10.6), la corriente total inducida por la corriente a cualquier frecuencia es P + I2Z, y sustituyendo Y = I/Z:

La V es una constante, ya que R-L-C se conecta en paralelo con una fuente de tensión AC. De la Fig. 10.15(b), en el punto cuando f = f0 se obtiene la admitancia mínima. Cuando f < f0 o cuando f > f0, la admitancia aumentará cuando la frecuencia se aleja lo suficiente de f0. De aquí podemos obtener el diagrama de potencia vs. frecuencia, como se muestra en la Fig. 10.20.
De las Fig. 10.20 y 10.15(a), encontramos que:
1. Cuando f < f0 o cuando f > f0, el circuito es capacitivo o inductivo. La reactancia inductiva no es igual a la reactancia capacitiva. Por lo tanto, la parte imaginaria de la admitancia se hará más grande, y la admitancia se hará más grande, también. De la Ecuación (10.15) sabemos que la potencia aumentará, también. Esto significa que las señales de salida de la fuente de tensión V tienen mayor potencia disipada en el circuito R-L-C paralelo.
Fig. 10.20 – Diagrama de potencia vs. frecuencia en circuito RLC paralelo
2. Cuando f = f0, el circuito es resistivo puro. La admitancia es mínima. De la ecuación (10.15) sabemos que la potencia es mínima en este momento. Esto significa que hay una disipación mínima de potencia en el circuito RLC.
Del análisis anterior sabemos que el significado de la curva de potencia en la Fig. 10.20 es que la fuente de tensión V disipa la potencia en el circuito RLC. Por lo tanto, hay una disipación mínima de potencia en el circuito RLC paralelo en el punto f0, y la mayoría de la potencia puede entregarse. Cuando f < f0 o cuando f > f0, y la frecuencia se aleja lo suficiente de f0, la potencia disipada en el circuito RLC paralelo se aumentará gradualmente. Esto significa que la salida de potencia se disminuirá gradualmente. La impedancia de resonancia y la respuesta corriente vs. frecuencia en el circuito R-L-C paralela son opuestos a los resultados del circuito R-L-C en serie. Por lo tanto, se le llama también como antiresonante.
Fig. 10.21 – diagrama de ancho de banda.
En la Fig. 10.21 correspondiente al diagrama del ancho de banda de la corriente, ésta tiene un mínimo I0 en el punto de resonancia. En el punto de ¸ veces la corriente existen dos frecuencias, f1 y f2, siendo la primera, la frecuencia de corte bajo , y f2 la frecuencia de corte alto. El ancho de banda BW es:
(a) Potencia vs. frecuencia (b) Admitancia vs. frecuencia
Fig. 10.22 – Corriente y admitancia en el ancho de banda.
Ejemplo 10.7. Se tiene un circuito paralelo resonante con V = 10Ð0º, R = 1 kW, L = 1 mH y C = 20 mF. Determine: (1) la frecuencia de resonancia, (2) la corriente en el punto de resonancia, (3) la corriente en la frecuencia de corte
Respuesta:

De la Ecuación (10.19) sabemos que Q = PL / PR o que Q = PC / PR. Por lo tanto, también sabemos que:
O que:
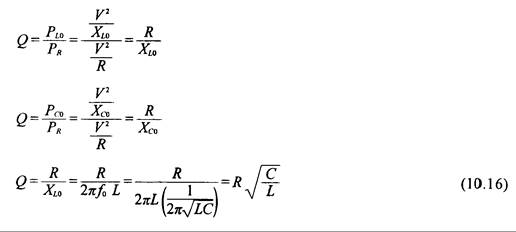
De la Ecuación (10.16) sabemos que Q es proporcional a la resistencia. Para obtener una Q alta, entonces es necesario que la resistencia se mantenga alta en el circuito paralelo. Se puede también elevar la relación de capacitancia a inductancia para obtener un Q más alto. En el punto de resonancia, V = I0R, las corrientes en el inductor y capacitor son respectivamente:

Sabemos que el propósito del circuito resonante es dejar salir del circuito solamente frecuencias particulares. Si el ancho de banda es muy amplio, entonces cualquier frecuencia puede pasar por el circuito, y la selectividad es pobre. No obstante, con un ancho de banda más angosto, se mejora la selectividad, como se muestra en la Fig. 10.23.
De las ecuaciones anteriores: Q = f0 / BW, o sea BW = f0 / Q podemos obtener ciertas conclusiones sobre el factor de calidad, ancho de banda, amplitud de la onda de corriente y selectividad como sigue:
1. Si Q es relativamente grande, el ancho de banda será relativamente angosto, la curva de la corriente se tornará más aguda y se mejora la selectividad, como se muestra en la Fig. 10.23 (BW1).
2. Si Q es relativamente pequeña, el ancho de banda será relativamente más ancho, la curva de la corriente se tornará más suave y se desmejora la selectividad, como se muestra en la Fig. 10.23 (BW2).
Fig. 10.23. Comparación de la selectividad
Ejemplo 10.8. En la Fig. 10.15(a), cuando V = 200Ð0º, R = 50 kW, L = 4 mH y C = 100 nF, determine: (1) factor de calidad, (2) corriente en el punto de resonancia, (3) el flujo de corriente a través del capacitor e inductor, (4) frecuencia de resonancia, y (5) ancho de banda.
Respuesta:
bajo
alto
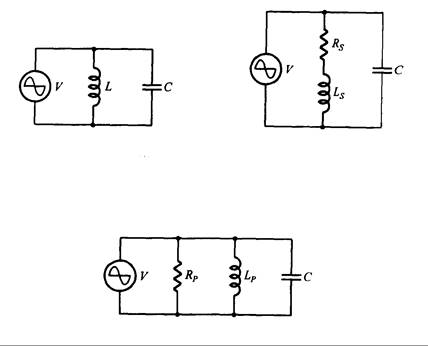
La utilidad de un circuito LC resonante en paralelo se muestra en la Fig. 10.24(a). El inductor se hace arrollando un alambre alrededor de una bobina, por lo tanto, el inductor no solamente tiene inductancia sino también resistencia, como se puede ver en la Fig. 10.24(b). Esta resistencia es mucho más pequeña que la impedancia del circuito. No obstante, cuando el circuito es resonante, la resistencia sí es muy importante. Por lo tanto, no se puede ignorar la resistencia durante el análisis del circuito. De igual forma para el capacitor, ya que el alambre y las placas tienen resistencia, pero debido a su valor bajo, la resistencia se puede ignorar.
Para analizar el circuito de la Fig. 10.24(b), lo convertiremos en un circuito R-L-C en paralelo, como se ve en la Fig. 10.25. Usamos la frecuencia resonante como base debido a que el valor de R es el que tiene una influencia más importante en este momento.
Fig. 10.25 – Circuito R-L-C equivalente en paralelo
(a) Resonancia de Inductor-capacitor (b) Resonancia real de Inductor -
en paralelo capacitor
Fig. 10.24 – Circuito útil en paralelo
Para convertir el circuito en serie resistencia – reactancia como se ve en la Fig. 10.26(a) a un circuito en paralelo resistencia – reactancia como en 10.26(b), la impedancia equivalente en los dos terminales debe ser igual. La impedancia de la resistencia – reactancia en serie es Z = RS ± j XS, y la impedancia de la resistencia – reactancia en paralelo es Y = GP ± jBp, donde Y = 1/Z.
(a) Circuito en Serie (b) Circuito en Paralelo
Fig. 10.26. Conversión de circuito resistencia – reactancia
de serie a paralelo
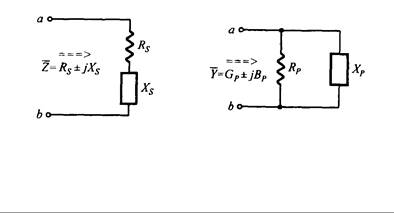
Cuando:
(a) Circuito paralelo (b) Circuito en serie
Fig. 10.27. Conversión de circuito resistencia – reactancia
de paralelo a serie
Si la reactancia en el circuito resistencia – reactancia en serie es capacitivo, entonces, de la Ecuación (10.17) y (10.18) sabemos que la reactancia equivalente en el circuito es:
En la Fig. 10.27(a) tenemos un circuito resistencia – reactancia en paralelo, que se convierte en otro circuito resistencia – reactancia en serie como se muestra en la Fig. 10.27(b). El método es el siguiente:
Como Y = Gp +/- jBp, entonces la parte real de la ecuación anterior es Gp y la parte imaginaria es Bp. Se puede obtener Rp y Xp
---Ver Libro de Texto---
(10.22)
Cuando el circuito en la Fig. 10.25 funciona a la frecuencia de resonancia, entonces:
---Ver Libro de Texto---
Por lo tanto, ---Ver Libro de Texto---
Reacomodando de tal forma que: ---Ver Libro de Texto---
Sustituyendo en la Ecuación (10.21):
---Ver Libro de Texto--- (10.23)
En el punto de resonancia XLS = XC,
---Ver Libro de Texto---
De la Ecuación (10.23):
---Ver Libro de Texto---
---Ver Libro de Texto--- (10.24)
En aplicaciones prácticas, cuando el factor de calidad es más alto de 10, entonces L es mucho más alta que C. Esto convierte a R2C/L en un valor pequeño, que se puede ignorar. Por lo tanto, cuando Q < 10 podemos usar la Ecuación (10.24) para calcular la frecuencia de resonancia. Cuando Q > 10 se puede ignorar R2C/L , y usar f0= ½ p Ö(LC).
El factor de calidad Q debe tener el mismo valor en circuitos R-L en serie y en el circuito R-L paralelo equivalente. Esto se comprueba de la siguiente forma:
---Ver Libro de Texto--- (10.25)
Ejemplo 10.9. Se conectan un capacitor con C = 100mF, L = 0.03 H y R = 2 W en paralelo con una fuente de tensión de v = 100Ð0º Voltios. Determine: (1) la frecuencia de resonancia f0, y (2) el factor de calidad.
Respuesta: ---Ver Libro de Texto---
Básicamente, los circuitos resonantes se diseñan para obtener buenos efectos en algunas frecuencias particulares. Otras frecuencias son rechazadas o su señal se atenúa. Por lo tanto, estos circuitos se llaman “filtros”. Estos filtros generalmente se usan en circuitos modernos de comunicación, y de los cuales existen cuatro tipos:
1. Filtros pasa - banda
2. Filtros parada – banda
3. Filtros pasa - bajos
4. Filtros pasa - altos
10.5.1 Filtros Pasa - Banda
En realidad, el filtro pasa – banda es un circuito RLC resonante en serie.
La entrada proviene de una fuente de tensión con diferentes frecuencias, y la salida se obtiene en el terminal de potencial de la resistencia, como se muestra en la Fig. 10.28. La respuesta de la corriente vs. frecuencia ya se discutió anteriormente, y la curva se muestra en la Fig. 10.29. En la frecuencia de resonancia f0, se tiene la corriente máxima.
Fig. 10.28 – Filtro pasa – banda Fig. 10.29. Curva de respuesta
Voltaje de salida V0
ajustable
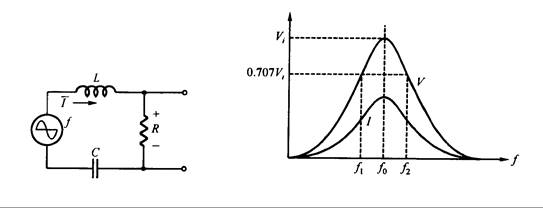
La tensión de salida entre los terminales de la resistencia se puede obtener mediante la Ley de Ohm, V0 = IR. De esta ley, vemos que la tensión es proporcional a la corriente, y la curva toma la forma que se muestra en la Fig. 10.29. En el punto de resonancia, la tensión de salida es un máximo y es igual a la tensión de entrada. Como se mencionó antes, se puede obtener hasta 0.707 veces la tensión máxima de salida en la frecuencia de corte f1 y f2, donde f2 – f1 es el ancho de banda BW. En frecuencias que se encuentren entre f1 y f2, la tensión de salida es bastante alta. Para señales con frecuencias menores de f1 o mayores de f2, las tensiones de salida son muy pequeñas. Esto significa que aquellas señales con frecuencias entre f1 y f2 son más fáciles de hacer pasar a través del circuito hacia la carga. Por lo tanto, a este circuito lo llamamos “filtro pasa – banda”.
El efecto de este filtro es opuesto al filtro pasa – banda. Es también un circuito RLC en serie pero la salida se obtiene de los terminales del inductor y el capacitor, como se ve en la Fig. 10.30.
![]()
en la frecuencia de
![]()
La tensión de
salida es igual a la tensión de entrada.
![]()
La tensión de
Salida de tensión V0
Fig. 10.30 – Filtro parada - banda
Fig. 10.31 – Curva de respuesta para filtro parada - banda
En la Fig. 10.32(a) y (b), la reactancia inductiva XL = 2 p fL es proporcional a la frecuencia y la reactancia capacitiva Xc = ½ p fC es inversamente proporcional a la frecuencia. Cuando la frecuencia de entrada es cero, XL = 0, Xc = ¥, y el circuito se considera como en cortocircuito, con una salida de tensión de cero.
De lo anterior, se puede dibujar la respuesta de la frecuencia de la tensión de salida como se muestra en la Fig. 10.33. Por lo tanto, cuando la frecuencia es menor de f2, la señal es más fácil de pasar por el circuito. Por esto se le llama “filtro pasa bajo”.
Fig. 10.33 – Respuesta de la frecuencia para filtro pasa - bajo
Fig. 10.32 – Filtro pasa - bajo
En la Fig. 10.34(a) y (b), cuando la frecuencia de entrada es cero, XL = 0, Xc = ¥, y la señal no puede pasar hacia la salida. Por lo tanto la tensión de salida es igual a cero. Ciando la frecuencia es infinita, Xc = o y el circuito se considera como en cortocircuito, siendo fácil de pasar la señal hacia la salida. Por lo tanto la tensión de salida es igual a la de entrada. La respuesta de la frecuencia de la tensión de salida como se muestra en la Fig. 10.35. Por lo tanto, cuando la frecuencia es mayor de f1, la señal es más fácil de pasar por el circuito. Por esto se le llama “filtro pasa alto”.
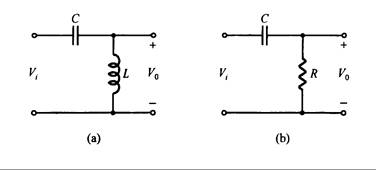
Fig. 10.34 – Filtro pasa - alto
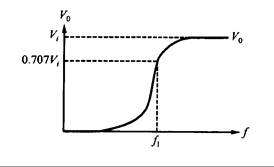
Fig. 10.35 – Respuesta de la frecuencia para un filtro pasa – alto
Estos filtros se pueden usar en diferentes aplicaciones, tal como separar las señales de audio y video en un aparato de televisión. La modulación de la onda portadora es como se muestra en la Fig. 10.36. Por lo general, cada canal de televisión tiene un ancho de banda de 6 MHz, donde unos 4 MHz son para la modulación de la señal de video, y se tiene un canal de modulación de audio en los 4.5 MHz. Por lo tanto, se requieren dos filtros para separar estas dos señales. Se pueden usar un circuito resonante paralelo L1C1 para obtener la separación del audio en 4.5 MHz, y usar un circuito resonante en serie L2C2 para lograr la separación de la salida de video en 4.5 MHz. La respuesta de la frecuencia es tal como se muestra en la Fig. 10.37.
Amplificador de audio y video
Salida de audio
(a) Banda de modulación (b) Circuito
Salida de video
Entrada de audio y video (A/V)
Señal de Señal de
Video audio
Fig. 10.36 – separación de audio y video en TV
(a) Respuesta L1C1 de señal de audio Señal L2C2 de video
Fig. 10.37 – Curvas de respuesta de audio y video
Señal de audio
Señal de video
Señal de audio
Señal de
video
I. Características de la resonancia R-L-C en serie
(1) Condición: XL = XC
(2) Impedancia de resonancia: Z = R (mínimo)
(4)Corriente de resonancia: I0 = V / Z0 = V / R (máximo
(5) Para f > f0, el circuito es inductivo.
(6) Para f < f0, el circuito es capacitivo
(7) Para f = f0, el circuito es resistivo
(10) Ancho de banda BW : ![]()
(11) Si Q es relativamente alto, la forma de la onda es más aguda, y se mejora la selectividad.
II. Características del circuito R-L-C resonante paralelo
(1) Condición : BL = BC, que es lo mismo que XL = XC
(2) Frecuencia de resonancia f0 = 1/ 2 pÖ(LC)
(3) Impedancia de resonancia Z = R (máximo), admitancia Y = G (mínimo)
(4) Corriente de resonancia I0 = V/Z = VY = V/R = VG = IR (mínimo)
(5) Para f > f0, el circuito es capacitivo.
(6) Para f < f0 el circuito es inductivo
(7) Para f = f0, el circuito es resistivo.
(8) Corrientes: IR = V/R = I0 , IC = V / XLO = v / XCO = QI0
(9) Factor de calidad : Q = BLO / G = BCO / G = RÖ(C/L)
(10) Ancho de banda BW : f2 – f1 = f0 / Q
(11) Si Q es relativamente alto, la forma de la onda es más aguda, y se mejora la selectividad.
III. El circuito equivalente de un inductor real es una resistencia interna R y un inductor puro L en serie.
IV. En un circuito LC resonante en paralelo real, si Q < 10 la frecuencia de resonancia fo = 1 / (2pÖ(LC) ) Ö(1-R2 C/L). Si Q > 10, la frecuencia de resonancia fo = 1 / (2pÖ(LC). El factor de calidad es: Q = XLO / R = 2 p fo L/R.
V. Los filtros pasa – banda y parada – banda son circuitos R-L-C en serie resonantes. Si la salida se obtiene de los terminales de la resistencia es un filtro pasa – bajo. Si la salida se obtiene de los terminales del inductor y capacitor en serie, se trata de un filtro parada – banda.
VI. Filtro pasa – bajo: deja pasar las señales de baja frecuencia y rechaza o atenúa al circuito con señales de alta frecuencia.
VII. Filtro pasa – alto: deja pasar las señales de alta frecuencia y rechaza o atenúa al circuito con señales de baja frecuencia.
1. Cuando una corriente AC en un circuito RLC en serie está en resonancia, la relación del fasor entre el potencial de terminal y la corriente es: _________
2. En un circuito L-C en serie, si está en resonancia, la impedancia del circuito es de ______W.
3. En un circuito L-C en paralelo, si está en resonancia, la impedancia del circuito es de ______W.
4. En un circuito RLC en serie, la frecuencia de resonancia es de _______ Hz.
5. En un circuito RLC en serie, la corriente de resonancia es de _______ Hz.
6. En un circuito RLC en serie, si la frecuencia es mayor que la frecuencia de resonancia, el circuito se comporta como ______.
7. En un circuito RLC en serie, la relación entre VL y VC es: _________.
8. En un circuito RLC en paralelo, si R=1KW, L=0.5H, C=200mF, entonces la frecuencia de resonancia es de ______.
9. Si la frecuencia de resonancia en serie de un circuito RLC es de 1 kHz, el factor de calidad es 20, entonces el ancho de banda es de ______ Hz.
10. En un circuito RLC en serie resonante, entre más pequeño sea R, el factor de calidad será ______.
11. En un circuito RLC en serie, si la frecuencia es menor que la frecuencia de resonancia, el circuito actúa como ______.
12. Anti-resonancia es : ______.
13. En un circuito RLC en paralelo, si la frecuencia es mayor que la frecuencia de resonancia, el circuito actúa como ______.
14. En un circuito RLC en paralelo resonante, entre más pequeño sea R, el factor de calidad será ______.
15. En un circuito RLC resonante, un factor de calidad alto significa: ______.
16. En un circuito RLC en serie, si R=5W, L=0.1H, C=50mF y el potencial en la fuente de tensión es de 100 V, entonces la corriente es ____A en el punto de resonancia.
17. Un circuito RLC en serie tiene 10 A en el punto de resonancia, entonces la corriente es de _____A en las frecuencias de corte.
18. El circuito de la Fig. 10.38(a) es : ______.
19. El circuito de la Fig. 10.38(b) es: _______.
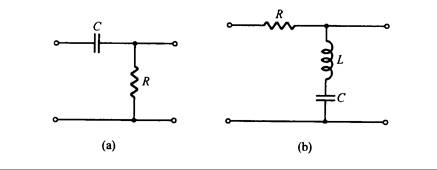
Fig. 10.38
1. Dibuje la curva de respuesta de frecuencia de la corriente del circuito L-C en serie, y explíquelo brevemente.
2. Explique las condiciones que hacen que un circuito L-C en serie o L-C en paralelo sean resonantes.
3. En la Fig. 10.39, determine: (1) frecuencia resonante, (2) impedancia resonante, (3) corriente resonante, (4) corriente en las frecuencias de corte, (5) potencial en cada uno de los dispositivos en resonancia, (6) potencia resonante, (7) factor de calidad, y (8) ancho de banda.
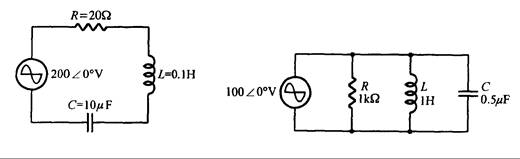
4. En la Fig. 10.40, determine: (1) frecuencia resonante, (2) admitancia resonante, (3) corriente resonante, (4) corriente en las frecuencias de corte, (5) potencial en cada uno de los dispositivos en resonancia, (6) potencia resonante, (7) factor de calidad, y (8) ancho de banda.
5. En la Fig. 10.41, determine: (1) frecuencia resonante, y (2) factor de calidad.
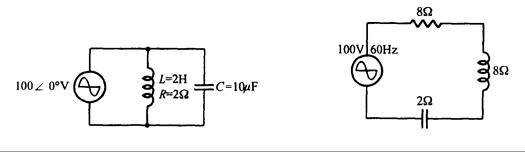
Fig. 10.41 Fig. 10.42
6. ¿Qué es un filtro pasa – banda? Dibújelo y explique.
7. ¿Qué es un filtro pasa – bajo? Dibújelo y explique.
8. ¿Qué es un filtro pasa – alto? Dibújelo y explique.
9. En la Fig. 10.42, determine: (1) frecuencia resonante, (2) impedancia resonante, (3) potencial en cada uno de los dispositivos en resonancia.
10. En un circuito R-L-C en serie se obtiene resonancia a una frecuencia de 60 Hz. Determine la capacitancia si L = 0.4 H.
11. En la Fig. 10.43, ¿cuál debe ser la inductancia para que haya resonancia en f = 2 kHz?

Fig. 10.43
12. Describa la relación entre factor de calidad y selectividad.
Fuente del documento: https://profejuandotcom.files.wordpress.com/2014/03/capc3adtulo-10-circuito-resonante.doc
Sitio para visitar: https://profejuandotcom.files.wordpress.com
Autor del texto: no especificado en el documento de origen o se indique en el texto
Las letras son propiedad de sus respectivos autores y les damos las gracias por la oportunidad que nos brindan para conocer sus textos libres para fines ilustrativos y educativos. Si usted es el autor del texto y que está interesado para solicitar la eliminación del texto o la inserción de otra información envíe un correo electrónico después de que los controles adecuados que va a satisfacer su solicitud tan pronto como sea posible.
Los resúmenes, toma nota de los textos que figuran en nuestra página web se ponen a disposición de forma gratuita con fines didácticos de la ilustración, científica, social, civil y cultural a todos los posibles interesados de acuerdo con el concepto de uso justo, y con el 'objetivo de cumplimiento de la Directiva Europea 2001/29 / CE y del «arte. 70 de la ley 633/1941 sobre derechos de autor
La información médica y de la salud en este sitio es de carácter general y para propósitos informativos solamente y por lo tanto no puede en ningún caso sustituir el consejo de un médico (o un autorizado legalmente a la profesión).