Resistencia eléctrica

 

 

Tensión y corriente eléctrica

Corriente continua y corriente alterna

Resistencia eléctrica

Ley de OHM

 

• Calcular la intensidad que circula por la resistencia de un circuito electrónico de 100Ω, cuando está sometida a una tensión de 4v.

     Solución: I = 40mA

 

 

 

• Determinar la resistencia que posee un circuito eléctrico, sabiendo que está sometido a una tensión de 20v, y que la corriente que circula por él es de 15mA.

     Solución: R = 1.3KΩ

• Se sabe que con la piel húmeda, la resistencia del cuerpo humano es muy pequeña (2500Ω). ¿Qué tensión será suficiente para provocar el paso de una corriente peligrosa de 30mA por el cuerpo humano, en estas condiciones?

     Solución: V = 75v

Potencia eléctrica

 

• Hallar la potencia que consume una resistencia limitadora al conectarla a una tensión de 12V, si su resistencia es de 1KΩ.

Solución: P = 144mW

• La potencia máxima que puede proporcionar un circuito eléctrico es de 25w. ¿Este circuito podrá proporcionar una corriente de 2A al conectarlo a una fuente de 20V?

Resistencias comerciales:

 

• Determinar la corriente que aparece en una lámpara incandescente al conectarla a una fuente de 380v, sabiendo que R.FRIO = 500Ω y que la R.CALIENTE = 900Ω. Calcular esta corriente en dos casos:

• Nada más conectar la lámpara.
• Una vez encendida.

    Soluciones: A) I = 0.76A;  B) I = 0.42A

• La tolerancia de una resistencia, nos indica los valores máximos y mínimos entre los que está comprendida la resistencia.

 

• Cuanto más pequeña sea la tolerancia de una resistencia, más cara es la misma.

 

• Se quiere determinar los valores entre los que puede estar comprendida una resistencia de 100Ω, si el fabricante asegura que esta posee una tolerancia de ±8%

• Hallar los valores entre los que está comprendida una resistencia de 500Ω, si el fabricante nos da una tolerancia de ±5%.

Solución: R = 475-525Ω

• Código de colores:

• El código consiste en una serie de anillos de colores pintados sobre el cuerpo de la resistencia, que nos permite obtener el valor de cada una de ellas.

 

 

 

 

• Los valores más típicos de tolerancia son oro y plata.

 

• Determinar el valor óhmico de las siguientes resistencias que aparecen con los colores:

• R1: rojo, violeta, naranja, plata.

• R2: marrón, rojo, naranja, rojo.

 

• R3: marrón, verde, gris, oro

 

• ¿Qué colores les correspondería a las siguientes resistencias?

• R1 = 24KΩ ± 5%

• R2 = 68MΩ ± 10%

• R3 = 110Ω ± 2%

                          Ejercicios de repaso

1. Calcular la corriente que circula por una resistencia eléctrica, cuyo valor es de 4.7KΩ, sabiendo que está sometida a una tensión de 10V.

Solución: I = 2mA

2. Calcular la resistencia eléctrica de un circuito, si se somete al mismo a una tensión de 12V y la corriente que circula por él es de 12mA.

Solución: R = 1KΩ

3. Calcular la tensión de funcionamiento de un horno eléctrico que posee una resistencia de 22Ω, y que, al ser conectado, se establece por él una intensidad de 5.7A.

Solución: V = 125.4v

4. Se dispone de una linterna que funciona con una pila de 1.5v; la lamparita tiene una resistencia de 50Ω. Calcular la intensidad y la potencia de la misma.

Solución: I = 30mA; P = 45mW

5. ¿Qué resistencia y potencia tiene una plancha eléctrica que consume 2A conectada a 220V?

Solución: R = 110Ω; P = 440W

6. Determinar el valor óhmico y la tolerancia de una resistencia que aparece con los colores:  rojo – azul – naranja - plata .

7. ¿Cuál es la cualidad por la que se diferencian los buenos conductores de los malos?

• Intensidad óhmica.
• Resistencia eléctrica.
• Tensión resistiva

8. ¿En qué momento será más alta la corriente eléctrica por una lámpara? JUSTIFICA LA RESPUESTA.

• Una vez encendida, ya que es cuando más consume.
• Justo al cerrar el interruptor.
• La corriente eléctrica es la misma en todo momento.

 

 

 

9. La unidad de medida de la tensión eléctrica es:

• El voltio
• El amperio.
• El watio

• Una plancha eléctrica tiene una potencia de 1000W y una tensión de 220V. Calcular el valor de su resistencia interna.

          Solución:  R = 48.35Ω

• Al conectar una lámpara a una toma de corriente de 100V se miden por el circuito 750mA. Determinar la potencia de la lámpara y su resistencia.

                   Solución: P = 75W;   R = 133Ω

• Se dispone de una lámpara de la que se conoce su potencia de trabajo (100W), y su resistencia interna (1.5Ω). ¿A qué tensión se podrá conectar la lámpara para que funcione correctamente?

           Solución: V = 12.2V

• ¿A qué tensión habrá que conectar una estufa de 750W si su resistencia interna es de 75Ω? ¿Cuál será la corriente que circula por la misma?

                Solución: V = 237v;  I = 3.16A

• Un calentador de agua presenta en su placa de características los siguientes datos: 3KW; 220V. Determinar:

• Intensidad de la corriente y resistencia interna

• La potencia que consume, si se conecta ahora a 125V, considerando que la resistencia permanece constante.

Soluciones:

• I = 13.6A;  R = 16.2Ω
• P = 968W

Cuestión 1:

¿Por qué no podemos transportar la energía eléctrica que sale directamente de los generadores?

 

 

Cuestión 2:

¿Por qué no podemos consumir la energía eléctrica que viene directamente de las líneas de transporte?

 

 

 

• Sistemas de Protección: Fusibles

 

• Es un elemento que se emplea para la protección contra cortocircuitos y sobrecargas de la red eléctrica.

 

• Estas sobrecargas se caracterizan por un gran aumento de la corriente, lo que puede dar lugar a la destrucción de los aparatos conectados a la misma, por exceso de calor.

• Un fusible está compuesto por un hilo conductor que tiene un grosor muy pequeño:

 

 

 

• Este pequeño grosor hace que posea una resistencia muy elevada. Al pasar una gran cantidad de corriente por esta resistencia tan elevada, se produce mucho calor, lo que hace que el fusible se funda.
• Al fundirse el fusible, la corriente queda cortada porque el circuito se ha abierto, evitando así que la corriente dañina estropee los componentes valiosos del circuito.

• Los fusibles se distinguen unos de otros por la cantidad de corriente que pueden soportar sin fundirse. Esta cantidad de corriente viene inscrita en el cuerpo del fusible:

 

 

 

 

Ejercicio:

La potencia máxima que proporciona un amplificador es de 400W. Determinar la intensidad del fusible necesario para la protección del mismo, si la tensión de la red es de 220V.

                                      Solución: I = 1.82A

 

 

 

ACTIVITATS
1.- Un cable de coure té una longitud de 5 km i una secció de 10 mm2. Calcula la resistència que ofereix al pas de la corrent elèctrica. Dada: ρcoure = 0,017 Ω·mm2/m
2.- Al cable anterior es vol tenir una resistència màxima de 5 Ω. De quina secció haurà de ser el cable?.
3.- Ompli els espais en blanc de la següent taula, segons corresponga:

Negre	0	RESISTÈNCIA	BANDA 1	BANDA 2	BANDA 3
Marró	1	10 Ω	Marró		Negre
Roig	2	22 Ω			Negre
Taronja	3		Marró	Negre	Marró
Groc	4		Roig	Roig	Taronja
Verd	5	470 Ω
Blau	6	560 Ω
Morat	7		Groc	Marró	Marró
Gris	8		Verd	Blau	Negre
Blanc	9		Marró	Negre	Negre

4.- Munta els següents circuits:

a) Mesura amb el polímetre la resistència entre els punts A i B i entre els punts C i D i anota els resultats.
b) Calcula aplicant les fórmules d’associació de resistències sèrie i paral·lel, la resistència entre els punts A i B i entre els punts C i D.
c) Compara i comenta els resultats obtinguts als dos apartats anteriors.
5.- Munta l’associació de bombetes en sèrie següent:

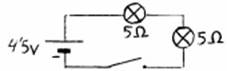
a) Mesura amb el polímetre la intensitat i anota el resultat.
b) Calcula la intensitat de la corrent elèctrica que circula per les bombetes utilitzant la llei d’Ohm.
c) Compara i comenta els resultats obtinguts als dos apartats anteriors.

6.- Munta l’associació de bombetes en paral·lel següent:

a) Mesura amb el polímetre la intensitat i anota el resultat.
b) Calcula la intensitat de la corrent elèctrica que circula per les bombetes utilitzant la llei d’Ohm.
c) Compara i comenta els resultats obtinguts als dos apartats anteriors.

7.- Munta l’associació de bombetes en sèrie següent:

a) Mesura amb el polímetre la intensitat i anota el resultat.
b) Calcula la intensitat de la corrent elèctrica que circula per les bombetes utilitzant la llei d’Ohm.
c) Compara i comenta els resultats obtinguts als dos apartats anteriors.

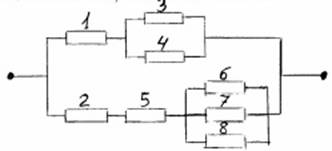
8.- A l’associació de resistències mixta de la figura, calcula la resistència total, tenint en compte els següents valors de les resistències:
    R1 = taronja, blanc, taronja  ,  R2 = groc, morat, taronja  ,  R3 = R4 = roig, roig, taronja  ,  R5 = marró, negre, roig  ,  R6 = R7 = marró, roig, marró  ,  R8 = groc, morat, marró.

9.- Què és un semiconductor?
10.- Què significa enllaç covalent?
11.- Què és un semiconductor intrínsec?
12.- Com s’obté un semiconductor extrínsec?
13.- Què diferències existeixen entre semiconductors tip N i tip P?
14.- A què diguem barrera de potencial a la unió P-N
15.- Explica el funcionament del díode. Dibuixa el seu símbol.
16.- Què aplicacions coneixes del díode?
17.- Realitza el muntatge següent i contesta:

a) Quin dels 2 LED s’encén? Perquè?
b) Què passaria si invertirem els polos de la pila?
c) Hauràs observat que al circuit hi ha connectada una resistència en sèrie a cada LED. Quina és la seua funció?. Què passaria si la lleva-se’m?. I si la resistència fora d’un valor molt més elevat?.

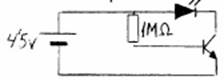
18.- Realitza el muntatge següent i contesta:

a) Per què el LED no s’encén?. Explica-ho aplicant la llei d’Ohm
b) Tracta de mesurar la corrent qui li aplega al LED amb el polímetre i anota-ho.

19.- Al circuit anterior, introdueix-li un element amplificador de corrent com és el transistor.

a) Per què el LED ara sí s’encén?. Explica-ho aplicant la llei d’Ohm i la fórmula del guany del transistor.
b) Mesura la corrent qui li aplega al LED amb el polímetre i anota-ho.

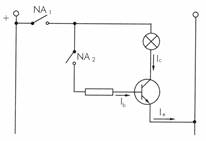
20.- Al circuit de la figura, explica (utilitzant la teoria del funcionament del transistor) el seu comportament quan es tanca NA1, i quan es tanca NA2.

21.- El guany d’un transistor és hfe = 1000 i la corrent que circula per la base és Ib = 2 mA. Calcula les corrents de col·lector Ic i d’emissor Ie.
22.- Calcula el guany d’un transistor sabent que la corrent d’emissor es Ie = 903 mA i la de col·lector Ic = 900 mA
23.- Quan es vol molta amplificació de corrent amb transistors, a què mètode es recorre?. Dibuixa l’esquema.
24.- Realitza el següent muntatge i explica què ha passat.

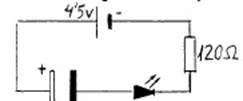
A continuació, lleva la pila i col·loca el LED al revés. Què ha passat ara al LED?. Explica-ho utilitzant la teoria de funcionament del condensador.
25.-Una part d’un circuit està formada per una associació de condensadors en paral·lel, els quals tenen els següents valors: C1 = 470 μF, C2 = C3 = 22 μF. Dibuixa l’associació i calcula la seua capacitat total.
26.- Si associem els condensadors de l’exercici anterior en sèrie. Quina serà la capacitat total?
27.- Calcula el temps que tardarà en descarregar-se un condensador de 470 μF mitjançant una resistència de 47 K.
28.- Al circuit de la figura, calcula la capacitat total de l’associació de condensadors mixta, i la constant de temps.

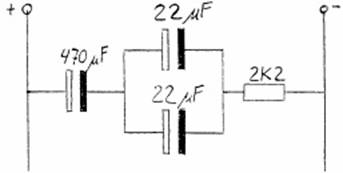
29.- Construeix un circuit temporitzador amb condensadors de 470 μF y 22 μF i una resistència de 22 K. El temps de retard que es vol aconseguir es de 11 s.