XI.  TURBOMACHINERY

This chapter considers the theory and performance characteristics of the mechanical devices associated with the fluid circulation.

General Classification:

Turbomachine -  A device which adds or extracts energy from a fluid.

Adds energy:                  Pump
Extracts energy:              Turbine

In this context, a pump is a generic classification that includes any device that adds energy to a fluid, e.g. fans, blowers, compressors.

We can classify pumps by operating concept:

1.  Positive displacement
2.  Dynamic (momentum change)

General Performance Characteristics

Positive Displacement Pumps
1.  Delivers pulsating or periodic flow (cavity opens, fluid enters, cavity closes, decreasing volume forces fluid out exit opening).
2.  Not sensitive to wide viscosity changes.
3.  Delivers a moderate flow rate.
4.  Produces a high pressure rise.
5.  Small range of flow rate operation (fixed pump speed).
Dynamic Pumps
1.  Typically higher flow rates than PDs.
2.  Comparatively steady discharge.
3.  Moderate to low pressure rise.
4.  Large range of flow rate operation.
5.  Very sensitive to fluid viscosity.
Typical Performance Curves (at fixed impeller speed)

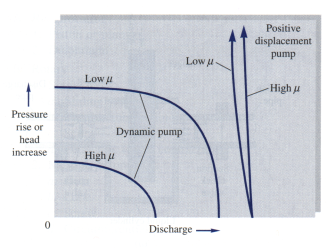
Fig. 11.2  Performance curves for dynamic and positive displacement pumps

Centrifugal Pumps
This is the most common turbomachine used in industry.  It includes the general categories of (a) liquid pumps, (b) fans, (c) blowers, etc.

They are momentum change devices and thus fall within the dynamic classification.

Typical schematic shown as

 

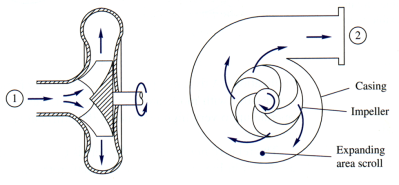
Fig. 11.3  Cutaway schematic of a typical centrifugal pump

Writing the energy equation across the device and solving for hp – hf ,we have

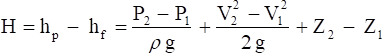
where  H is the net useful head delivered to the fluid, the head that results in pressure, velocity, and static elevation change.

Since for most pumps (not all),  V1 = V2  and  DZ  is small, we can write

Since friction losses have already been subtracted, this is the ideal head delivered to the fluid.  Note that velocity head has been neglected and can be significant at large flow rates where pressure head is small.

The ideal power to the fluid is given by

Pw = r Q g H

 

The pump efficiency is given by

where   BHP = shaft power necessary to drive the pump
w  =  angular speed of shaft
T = torque delivered to pump shaft

Note that from the efficiency equation, pump efficiency is zero at zero flow
rate Q and at zero pump head, H.

Basic Pump Theory

Development of basic pump theory begins with application of the integral conservation equation for moment-of-momentum previously presented in Ch. III.

Applying this equation to a centrifugal pump with one inlet, one exit, and uniform properties at each inlet and exit, we obtain

where              is the shaft torque needed to drive the pump
  are the absolute velocities at the inlet and exit of the pump

Thus, the applied torque is equal to the change of angular momentum across the device.

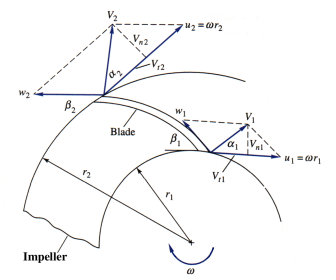
Fig. 11.4  Inlet and exit velocity diagrams for an idealized
pump impeller

Since the velocity diagram is key to the analysis of the device,  we will discuss the elements of the diagram in detail.
1.  At the inner radius r1 we have two velocity components:

a.  the circumferential velocity due to the impeller rotation    blade tip speed at inner radius b.  relative flow velocity tangent to the blade       tangent to the blade angle   These combine to yield the absolute inlet velocity  V1  at angle  a1

The absolute velocity can be resolved into two absolute velocity components:

1.  Normal ( radial ) component:

Note that for ideal pump design,

2.  Absolute tangential velocity:

again, ideally

It is also important to note that    is used to determine the inlet flow rate, i.e.,

where   b1   is the inlet blade width.

Likewise for the outer radius r2  we have the following:

a.  the circumferential velocity due to the impeller rotation   blade tip speed at outer radius b.  relative flow velocity tangent to the blade tangent to the blade angle   These again combine to yield the absolute outlet velocity  V2  at angle  a2

The exit absolute velocity can also be resolved into two absolute velocity components:

1.  Normal ( radial ) component:

Note that Q is the same as for the inlet flow rate

2.  Absolute tangential velocity:

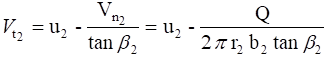
where        

Again,  each of the above expressions follows easily from the velocity diagram, and the student should draw and use the diagram with each pump theory problem.

We can now apply the moment - of – momentum equation.

    (again  Vt1 is zero for the ideal design)

For a sign convention, we have assumed that Vt1  and Vt2  are positive in the direction of impeller rotation.

The “ ideal” power supplied to the fluid is given by

or

Since these are ideal values, the shaft power required to drive a non-ideal pump is given by

The head delivered to the fluid is

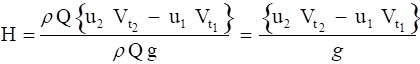
For the special case of purely radial inlet flow

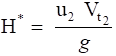
From the exit velocity diagram, substituting for Vt2 we can show that

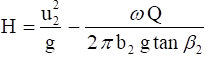      has the form         C1  -  C2 Q

where: C1  =

C1=shutoff head, the head produced at zero flow, Q = 0

Example  11.1:
A centrifugal water pump operates at the following conditions:
speed = 1440 rpm,  r1 = 4 in, r2 = 7 in,  b1 = 30o, b2 = 20o, b1 = b2 = 1.75 in
Assuming the inlet flow enters normal to the impeller (zero absolute tangential velocity):
find:  (a) Q, (b)  T, (c) Wp, (d) hp, (e) DP

Calculate blade tip velocities:

Since the design is ideal, at the inlet a1 = 90o,    Vt1 = 0 Vn1 = U1 tan 300 = 50.3 tan 30o = 29.04 ft/s

This is the flow rate for ideal design or Vt1 = 0 and a1 = 90˚.
Repeat for the outlet:

 

We are now able to determine the pump performance parameters.  Since for the centrifugal pump, the moment arm  r1  at the inlet is zero, the momentum equation becomes

This is the ideal torque delivered to the fluid.

Ideal power delivered to the fluid:
 
Note that for a real (non-ideal) pump the input power (motor size) required would be greater proportional to the efficiency of the pump. 
Head produced by the pump (ideal):

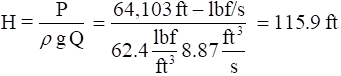
Pressure increase produced by the pump: