I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Quando un liquido viene riscaldato fino a raggiungere la temperatura di saturazione relativa alla pressione a cui il liquido stesso si trova, si manifesta il fenomeno dell’ebollizione; viene considerata una forma di scambio termico convettivo a causa della presenza di moto all’interno del fluido. L’ebollizione differisce dalle altre forme di scambio termico convettivo per la dipendenza sia dal calore latente di vaporizzazione del fluido che dalla tensione superficiale all’interfaccia liquido-vapore in aggiunta alle proprietà del fluido in ciascuna fase.
Si noti che, in condizioni di equilibrio (a pressione costante), durante l’ebollizione è possibile trasferire un’elevata quantità di calore senza che la temperatura si modifichi durante il passaggio di fase (trasformazione isoterma). Nella pratica, è necessario mantenere una certa differenza tra la temperatura di parete Tp e la temperatura di saturazione del liquido Tsat perché si abbia un consistente scambio termico.
Nel pool boiling il fluido è fermo ed ogni suo movimento è dovuto a moti convettivi naturali, mentre il moto delle bolle di vapore avviene a causa del galleggiamento. Consideriamo il contenitore d’acqua in figura 1.1 riscaldato su un fornello a gas e ne valutiamo gli effetti quando la temperatura di parete Tp è maggiore della temperatura di saturazione dell’acqua Tsat. Chiameremo ΔTe la differenza di temperatura (Tp-Tsat). Possiamo quindi scrivere la solita legge di raffreddamento di Newton:
Nella pratica industriale il fenomeno del pool boiling è sfruttato nell’ autoclave fig. 1.1 e nella caldaia Cornovaglia fig. 1.2.
|
|
Figura 1.1: Contenitore d’acqua riscaldato |
Figura 1.2: Caldaia Cornovaglia |
In figura 1.3 è mostrato un grafico che mette in relazione ΔTe con il flusso di calore q.
Figura 1.3: curva di ebollizione, dove è stata posta Tw=Tp.
ATTENZIONE: ogni esperimento ha la sua curva, quindi non si può utilizzare questa curva per ricavare ΔTe a partire da qs e viceversa. Per farlo bisogna utilizzare le espressioni analitiche indicate più avanti.
Possiamo distinguere in questo diagramma diversi regimi di ebollizione all’aumentare di ΔTe:
Zona 1-A: ebollizione in convezione naturale. |
|
In questa zona si ha un tratto lineare (h costante) caratterizzato da un basso scambio di calore. L’ebollizione anche se sta avvenendo non produce nessun particolare effetto fluidodinamico. |
Zona A-B: ebollizione nucleata. |
|
Si ha formazione di bolle che tendono rapidamente a far aumentare lo scambio termico. Le bolle salendo trascinano con se il fluido producendo dei moti convettivi, facendo aumentare lo scambio termico. In questa zona ho un brusco incremento della pendenza della curva che descrive un significativo aumento di h fino ad arrivare al suo valore massimo in B. |
Zona B-P: ebollizione nucleata. |
|
Le bolle salgono in colonne e grappoli e lo scambio termico continua ad aumentare in modo ancora più rapido. Ho ancora delle bolle distinte. |
Zona P-C: ebollizione a getti. |
|
Le bolle diventano talmente numerose e vicine tra loro da ostacolare lo scambio termico. Si formano dei getti di vapore stabili. Si parla di ebollizione a getti e non più nucleata. L’effetto trascinante tra bolle e fluido cala. Si nota infatti un calo della pendenza della curva di scambio termico. In P abbiamo un cambiamento di curvatura, questo comporta che, con un aumento di ΔTe abbiamo una diminuzione del coefficiente di convezione h. Questo fenomeno è causato dal contatto diretto tra il vapore e la superficie riscaldante (scambio termico in parete asciutta) a macchie di leopardo: il vapore, infatti, avendo una conducibilità termica molto minore del liquido, ostacola lo scambio termico. Le porzioni di parete asciutte tendono quindi a surriscaldarsi causando un effetto di stress termico/meccanico. |
Zona C-D: regime di transizione di ebollizione. |
|
Dal punto C (punto critico) dove si ha il massimo valore di flusso, ogni incremento di ΔTe non è sufficiente a compensare il decremento del coefficiente di convezione h; quindi la curva ha pendenza negativa e lo scambio termico diminuisce. La porzione di superficie asciutta aumenta bruscamente fino ad arrivare nel punto D (punto di Leidenfrost) dove ho la formazione di un film di vapore che presenta un’elevata resistenza termica. |
Zona oltre D: ebollizione a film. |
|
Superato il punto D (dove si ha il minimo flusso), questo comincia ad aumentare nuovamente perché lo scambio alla parete avviene attraverso uno strato di vapore per irraggiamento (l’irraggiamento diventa importante dopo il punto C) |
Consideriamo adesso la seguente figura:
Figura 1.4: percorsi di ebollizione a controllo di temperatura o di flusso
Da questa figura possiamo notare due andamenti diversi in funzione del tipo di controllo:
Allo stesso modo si ha lo shock termico quando si abbassa il flusso di calore al di sotto del punto D di minimo flusso, anche se in questo caso lo shock risulta essere molto meno pericoloso perché avviene a temperature minori (il salto è infatti circa da 200°C a 10°C).
A causa di questa isteresi, la caldaia viene progettata per lavorare sotto il punto B: si lavora cioè sempre in ebollizione nucleata, garantendo che la parete riscaldante resti sempre bagnata e che quindi lo scambio termico sia convettivo.
L’unico caso in cui viene applicato questo tipo di controllo è nelle caldaie per alimentare le turbine a vapore nelle navi militari, dove se devo avere molta potenza in poco tempo (ad esempio per scappare dalla nave nemica) supero il punto C: il rischio di essere abbattuti dai nemici rende infatti superfluo il rischio di esplosione della caldaia!
Per la zona A-P (ebollizione nucleata), al fine di ricavare il flusso di calore si utilizza la formula di Rohsenow, che vale alla temperatura di saturazione Tsat:
[W/m2]
Dove:
= viscosità dinamica del liquido [Pa*s]
= densità del liquido [kg/m3]
= densità del vapore [kg/m3]
= tensione superficiale del fluido [N/m2]
La tensione superficiale tende a far restare le bolle attaccate alla superficie. Una minor tensione superficiale quindi tende a far staccare le bolle dalla superficie, cosicché la superficie rimane bagnata e lo scambio termico rimane alto.
A seguire sono proposte delle tabelle dove si riscontrano i valori di Csf per varie combinazioni di fluido/materiale e della tensione superficiale 
dell’acqua a varie temperature.
Al punto C (massimo flusso) si può usare la seguente formula:
[W/m2]
Al punto D (minimo flusso) si può usare la seguente formula:
[W/m2]
I valori di 
e di 
vengono utilizzati per la progettazione del bruciatore come parametri di sicurezza.
Per la zona C-D (ramo di discesa) abbiamo invece a disposizione una relazione per ricavare il numero di Nusselt (questa formula vale quindi per la convezione)
Dove D [m] è il diametro del filo di Nichel o Platino, in quanto i film di vapore non riusciamo a ottenerli stabilmente sul fondo del recipiente ma solo riscaldando fili di Nichel o Platino per via elettrica.
Inoltre:
= viscosità cinematica del vapore [m2/s]
= conducibilità termica del vapore [J/(s*m*K)]
E r’ è il calore latente di vaporizzazione corretto, e si calcola come segue:
[J/kg]
La formula è calcolata con le proprietà termofisiche alla temperatura media del film Tmf, definita come segue:
[K]
Dati:
Sia data una pentola in acciaio riempita con 5l di acqua (figura 1.1) la quale viene portata ad ebollizione tramite l’utilizzo di un fornello elettrico. Le caratteristiche del contenitore e dell’acqua alla temperatura di saturazione (100 °C) sono le seguenti:
= 958,4 kg/m3
= 0,5975 kg/m3
= 58,9*10-3 N/m
= 281*10-6 Pa*s
Si vuole determinare:
Svolgimento:
Innanzitutto dobbiamo calcolare ΔTe, ovvero la differenza di temperatura Tp-Tsat:
Poiché con un tale valore di ΔTe dal figura 1.3 vediamo che siamo circa nella zona A-P, dobbiamo usare la (1) però valutare il flusso di calore scambiato:
[W/m2]
La potenza termica scambiata risulta pari a:
Tale Potenza è molto alta, in Italia fuori range operativo: in Italia, infatti, la massima potenza elettrica ad uso civile è pari a 6 kW.
Calcoliamo ora il coefficiente di convezione:
La portata in massa di vapore risulta pari a :
Considerando che 5 litri di acqua pesano circa 5 kg (quindi M=5 kg), il tempo di ebollizione si calcola come segue:
Utilizzando le relazioni (2), (3) e sostituendo al loro interno i valori numerici si possono ottenere i valori di flusso massimo e flusso minimo:
Come si può notare dal diagramma di figura 1.2, il valore di flusso a cui stiamo operando risulta essere troppo elevato, data la sua vicinanza al punto critico, quindi per allontanarci da esso ed operare in condizioni di sicurezza bisogna diminuire il valore di ΔTe. Ad esempio se operiamo con:
ΔTe = 9°C
Si ottiene:
Quindi la potenza termica è molto inferiore rispetto al caso precedente: 7 kW è un valore tipico di un fornello elettrico ad induzione, che però si può utilizzare solo nei paesi nordici, dove le abitazioni hanno una fornitura elettrica di 10-15 kW, mentre in Italia la maggior parte delle abitazioni ha circa 3 kW di potenza massima, e solo grazie ad un contratto maggiormente oneroso si possono avere 6 kW, che sono comunque insufficienti al funzionamento dei fornelli elettrici.
La portata in massa di vapore risulta pari a:
Il tempo di completa ebollizione:
Dati:
Sia dato un filo di metallo (esempio nichel o platino) il quale viene riscaldato elettricamente tenendolo immerso in acqua satura ad una temperatura di 100°C. Le caratteristiche del filo e dell’acqua alla temperatura di saturazione (100°C) sono le seguenti:
= 0,0331 W/(m*K)
= 957,4 kg/m3
= 4,81 kg/m3
= 58,9*10-3 N/m
= 279*10-6 Pa*s 
= 5,67*10-8
Si vuole determinare Q, ovvero la potenza termica che deve fornire la resistenza elettrica.
Svolgimento:
Innanzitutto dobbiamo calcolare ΔTe, ovvero la differenza di temperatura Tp-Tsat :
Dal diagramma di figura 1.3 si nota che per un valore di ΔTe> 100 °C (in prossimità del punto di flusso minimo) il flusso di calore scambiato avviene anche per irraggiamento. La relazione generale che tiene conto dello scambio radiante è la seguente (formula empirica):
Questa equazione non è risolvibile analiticamente (infatti htot è diverso da hconv+hirr), quindi si ricorre a relazioni ancor più approssimate. La seguente formula vale nel caso in cui hirr< hconv (condizione che come vedremo rispecchia il caso in cui ci troviamo):
Utilizzando la relazione (4) e sostituendo al suo interno i valori numerici si ottiene un valor medio del coefficiente di convezione (hconv):
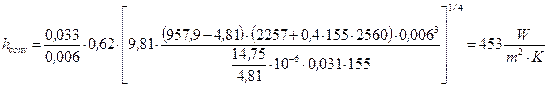
Il coefficiente di scambio termico per irraggiamento vale (vedi anche lezione del 8/3/2013):
Si nota come hirr<hconv quindi è possibile utilizzare la formula approssimata vista precedentemente ottenendo:
La potenza termica totale scambiata dalla superficie risulta pari a:
Fonte: http://pcfarina.eng.unipr.it/Public/Termofluidodinamica/Dispense-2013/13_Mosna_244183_Aldrighetti_243945.doc
Sito web da visitare: http://pcfarina.eng.unipr.it
Autore del testo: Bertorelli
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve
