I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Il processo di ossidazione di una specie chimica corrisponde alla perdita di elettroni da parte di quest’ultima.
Esempio:
Zn(s)® Zn2+ + 2e
Il processo di riduzione di una specie chimica corrisponde all’acquisto di elettroni da parte di quest’ultima.
Esempio:
Cl2(g) + 2e ® 2Cl-
In generale in un qualunque processo ossido-riduttivo (redox) vengono coinvolte almeno due specie di ossido-riduzione (coppie redox).
Per cui è sempre possibile, per ciascuna coppia di ossido-riduzione, scrivere la seguente reazione:
Ox + ne = Red (semireazione di ossido-riduzione)
Come convenzione si usa sempre scrivere la reazione di ossido-riduzione nel senso della riduzione.
E’ da notare la forte analogia tra le reazioni di ossido-riduzione e le reazioni acido-base, relativamente al concetto di coppia e, soprattutto, nel non ammettere la presenza di specie cariche libere in soluzione.
Perché si abbia trasferimento di elettroni da una specie all’altra occorre che il numero degli elettroni ceduti da una coppia di ossido-riduzione sia uguale al numero degli elettroni acquistati dalla seconda coppia di ossido-riduzione.
E’, quindi, possibile scrivere le due semireazioni di ossido-riduzione:
Ox1 + n1e = Red1 (semireazione di riduzione)
Red2 = Ox2 + n2e (semireazione di ossidazione)
Il processo globale sarà, dunque, la reazione di ossido-riduzione globale:
n2Ox1 + n1Red2 = n1Ox2 + n2Red1
Tenendo in considerazione che elettroni liberi in soluzione non sono ammessi.
La realizzazione di una reazione di ossido-riduzione, cioè il trasferimento di elettroni, può avvenire o per via chimica (mescolamento diretto delle due soluzioni), oppure per via elettrochimica (mediante la realizzazione di una pila).
Esempio:
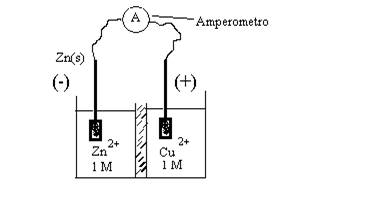
Scrivere le semireazioni di ossido-riduzione che sono alla base del funzionamento della pila Daniell.
Il processo di ossido-riduzione globale relativo al funzionamento della pila Daniell è:
Zn(s) + Cu2+ = Zn2+ + Cu(s)
Polo(+) = “arrivo” (consumo o sottrazione) di elettroni = semireazione catodica = semireazione di riduzione
Cu2+ + 2e = Cu(s)
Polo(-) = “partenza” (produzione) di elettroni = semireazione anodica = semireazione di ossidazione
Zn(s) = Zn2+ + 2e
Esempio:
Scrivere le semireazioni di ossido-riduzione che sono alla base del funzionamento della pila a secco (Leclanchè).
Il processo di ossido-riduzione globale relativo al funzionamento della pila Leclanchè è:
2MnO2(s) + Zn(s) + 2H3O+ = 2MnOOH(s) + Zn2+ + 2H2O
Polo(+) = “arrivo” (consumo o sottrazione) di elettroni = semireazione catodica = semireazione di riduzione
2MnO2(s) + 2H3O+ + 2e = 2MnOOH(s) + 2H2O
Polo(-) = “partenza” (produzione) di elettroni = semireazione anodica = semireazione di ossidazione
Zn(s) = Zn2+ + 2e
La pila è così schematizzata:
(-) Zn / NH4Cl, 10% (amido) / MnO2 / C (+)
Analogamente agli equilibri acido-base, dove una sostanza ha la tendenza a cedere o ad acquistare protoni, certe considerazioni possono essere fatte anche per gli equilibri di ossido-riduzione.
Ogni sostanza, infatti, ha la tendenza a cedere o ad acquistare elettroni.
Poiché per gli equilibri acido-base non esistono protoni liberi in soluzione, anche per gli equilibri di ossido-riduzione, non esistono elettroni liberi in soluzione.
La tendenza di una sostanza ad acquistare elettroni (potere ossidante) si misura facendo riferimento alla costante relativa alla reazione:
Nello studio degli equilibri di ossido-riduzione, si ipotizzerà che le attività coincidono con le concentrazioni (soluzioni diluite o presenza di un mezzo ionico costante).
ELETTRODI E POTENZIALI ELETTRODICI
Una lamina di un metallo immersa in una soluzione dei suoi ioni, assume un potenziale che dipende dalla natura del metallo e dalla concentrazione degli ioni presenti nella soluzione. Il potere ossidante di una sostanza si può misurare attraverso tale potenziale elettrico.
Così una lamina di zinco immersa in una soluzione contenente ioni Zn2+, ad esempio di Zn(NO3)2, assume una polarità negativa rispetto alla soluzione, in quanto avviene la semireazione:
Zn(s) → Zn2+ + 2e
Per il rame, invece, nel caso della pila Daniell, accade il contrario.
MISURA DEL POTENZIALE DI UN ELETTRODO
Non è possibile misurare il potenziale assoluto di un singolo elettrodo in quanto elettroni liberi in soluzione non esistono. E’ possibile misurare solo differenze di potenziali. Per fare ciò si realizza un’opportuna cella di cui una delle due semicelle, semicella di riferimento, è costituita da un elettrodo di metallo inerte (Pt) immerso in una soluzione acida e sul quale si fa gorgogliare H2. La semicella, così realizzata, è quella ad idrogeno che si basa sulla semireazione di ossido-riduzione:
H+ + e = (1/2)H2(g)
In accordo a quanto detto in precedenza, il potenziale di un elettrodo dipende dalla concentrazione degli ioni in soluzione, quindi occorre definire tale concentrazione. La condizione sperimentale nella quale tutte le specie ioniche si trovano a concentrazioni unitarie e le pressioni parziali di tutte le specie gassose sono anch’esse unitarie si chiama stato standard.
Il potenziale di conseguenza assunto da un elettrodo in tali condizioni sperimentali si chiama potenziale standard e si indica con il simbolo e°.
Nel caso della semicella ad idrogeno si attribuisce, arbitrariamente, potenziale di elettrodo zero quando [H+] = 1M e p(H2) = 1Atm.
Volendo misurare il potenziale di un elettrodo di zinco immerso in una soluzione dei suoi ioni in concentrazione 1M, occorre realizzare la pila:
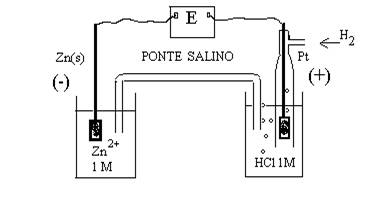
Si osserva, sperimentalmente, che l’elettrodo di Zn assume un potenziale negativo, in quanto col passare della corrente nel circuito la soluzione di zinco si concentra di ioni Zn2+. Quando si raggiunge l’equilibrio della reazione, che corrisponde alla condizione per cui non c’è più passaggio di corrente attraverso il filo conduttore esterno, la forza elettromotrice (f.e.m.), E°, vale + 0.763V.
La forza elettromotrice della pila è data da:
E° =e°(+)- e°(-) = e°H – e°Zn
In base alla definizione data in precedenza, si ha che e°H = 0.00V, quindi segue che e°Zn = - E° = - 0.763V.
La pila così realizzata prende il nome di elemento galvanico.
In tal modo si realizza la scala elettrochimica dei semielementi galvanici.
Potenziali di riduzione di alcuni semielementi galvanici
Semireazione |
e°, V |
Au3+ + 3e = Au(s) |
+ 1.50 |
Ag+ + e = Ag(s) |
+ 0.799 |
Cu2+ + 2e = Cu(s) |
+ 0.337 |
H+ + e = (1/2)H2(g) |
0.000 |
Pb2+ + 2e = Pb(s) |
- 0.126 |
Zn2+ + 2e = Zn(s) |
- 0.763 |
Al3+ + 3e = Al(s) |
- 1.50 |
Ca2+ + 2e = Ca(s) |
- 2.87 |
I valori degli e° con i relativi segni danno informazioni, nel momento in cui si realizza un elemento galvanico, sulla semireazione di riduzione e sulla semireazione di ossidazione.
In particolare la semireazione di riduzione ha luogo in corrispondenza del valore di e° più positivo.
DIPENDENZA DEL POTENZIALE ELETTRODICO DALLA CONCENTRAZIONE DELLE SPECIE DI OSSIDO-RIDUZIONE
In generale per un processo di ossido-riduzione, che ha luogo in un semielemento galvanico, del tipo:
alla temperatura T il potenziale del semielemento è ben rappresentato dall’equazione:
e = e° + (RT/nF)ln([Ox]/[Red])
dove R = costante dei gas (8.314JK-1mol-1)
T = temperatura assoluta (298.15K)
n = numero di elettroni scambiati nel processo ossido-riduttivo
F = costante di Faraday (96500C/mol)
Tenendo conto di ciò e, inoltre, sapendo che ln(x) = 2.3026log(x), si ha:
e = e° + (0.05916/n)log([Ox]/[Red])
L’equazione definita rappresenta l’equazione di Nernst relativamente ad un processo ossido-riduttivo che ha luogo per un semielemento galvanico.
In particolare per la semireazione:
Tl3+ + 2e = Tl+
l’equazione di Nernst assume l’espressione:
e = e° + (0.05916/2)log([Tl3+]/[Tl+])
Nel caso di semireazioni in cui compaiano fasi condensate pure, solide oppure liquide, la loro attività è considerata unitaria.
Esempio:
Scrivere l’equazione di Nernst per la reazione di riduzione di Cu2+ a Cu(s), sapendo che e°(Cu2+/Cu) = + 0.337V.
La reazione da considerare è:
Cu2+ + 2e = Cu(s)
L’equazione di Nernst relativamente al semielemento è:
e = e° + (0.05916/2)log([Cu2+]/{Cu}) = e° + (0.05916/2)log[Cu2+]
Per le sostanze gassose si sostituiscono alle concentrazioni le pressioni parziali.
Esempio:
Scrivere l’equazione di Nernst per la reazione di riduzione di Cl2(g) a Cl-, sapendo che e°(Cl2/Cl-) = + 1.36V.
La reazione da considerare è:
Cl2(g) + 2e = 2Cl-
L’equazione di Nernst relativamente al semielemento è:
e = e° + (0.05916/2)log([Cl2]/[Cl-]2) = e° + (0.05916/2)log(p(Cl2)/[Cl-]2)
Nel caso in cui le semireazioni richiedano per il bilanciamento ioni H+ o altre specie, il potenziale dipende anche dalla concentrazione di tali specie.
Esempio:
Scrivere l’equazione di Nernst per la reazione di riduzione di MnO4-, in ambiente acido, a Mn2+ sapendo che e°(MnO4-/Mn2+) = + 1.49V.
La reazione da considerare è:
MnO4- + 8H+ + 5e = Mn2+ + 4H2O
L’equazione di Nernst relativamente al semielemento è:
e = e° + (0.05916/5)log([MnO4-][H+]8/[Mn2+])
Esempio:
Scrivere l’equazione di Nernst per la reazione di riduzione di Cr2O72-, in ambiente acido, a Cr3+ sapendo che e°(Cr2O72-/Cr3+) = + 1.33V.
La reazione da considerare è:
Cr2O72- + 14H+ + 6e = 2Cr3+ + 7H2O
L’equazione di Nernst relativamente al semielemento è:
e = e° + (0.05916/6)log([Cr2O72-][H+]14/[Cr3+]2)
Esempio:
Scrivere l’equazione di Nernst per la reazione di riduzione di BrO3-, in ambiente acido, a Br2(l) sapendo che e°(BrO3-/Br2(l)) = + 1.52V.
La reazione da considerare è:
BrO3- + 6H+ + 5e = (1/2)Br2(l) + 3H2O
L’equazione di Nernst relativamente al semielemento è:
e = e° + (0.05916/5)log([BrO3-][H+]6/{Br2}1/2) =
e° + (0.05916/5)log([BrO3-][H+]6)
CALCOLO DELLA F.E.M. DI UN ELEMENTO GALVANICO
Una cella elettrochimica, o elemento galvanico, si rappresenta scrivendo il polo negativo a sinistra. Le separazioni tra fasi sono indicate da una barra, mentre l’esistenza di un ponte salino, che garantisce il contatto elettrico tra le due soluzioni ma non il loro mescolamento, si rappresenta con due barre.
In accordo alla convenzione definita, la pila Daniell, si rappresenta secondo la forma:
(-) Zn / Zn2+, 1M // Cu2+, 1M / Cu (+)
Per valutare la f.e.m. di una pila, E, in condizioni diverse da quelle standard, occorre calcolare dapprima i potenziali dei singoli semielementi con l’equazione di Nernst e poi applicare l’equazione:
E = e(+)- e(-)
dove e(+)>e(-)
In altri termini si calcola il potenziale di ciascun semielemento in accordo all’equazione di Nernst poi si sottrae al potenziale “più positivo” il potenziale “più negativo”.
Esempio:
Calcolare la f.e.m. della pila Daniell, quando tutte le specie che prendono parte alla reazione si trovano nello stato standard, sapendo che e°(Cu2+/Cu) = + 0.338V e che e°(Zn2+/Zn) = - 0.763V.
La reazione da considerare confrontando i valori di e° è:
Zn(s) + Cu2+ = Zn2+ + Cu(s)
Per cui l’espressione della f.e.m. è:
E = e(+)- e(-) = eCu- eZn = e°Cu- e°Zn = + 0.338V - (- 0.763V) =
+ 1.101V
Esempio:
Calcolare la f.e.m. della pila Daniell, sapendo che [Cu2+] e [Zn2+] valgono rispettivamente 0.01M e 0.05M e inoltre e°(Cu2+/Cu) = + 0.338V e che e°(Zn2+/Zn) = - 0.763V.
Poiché le specie non si trovano nello stato standard, per assegnare la polarità della pila e, quindi, per stabilire quale specie si ossida e quale specie si riduce, bisogna dapprima calcolare per ciascun semielemento l’equazione di Nernst.
Applicando l’equazione di Nernst per la semireazione del rame si ha:
eCu = e°Cu + (0.05916/2)log[Cu2+] =
+ 0.338 + (0.05916/2)log(0.01) = + 0.279V
Analogamente per lo zinco si ha:
eZn = e°Zn + (0.05916/2)log[Zn2+] =
- 0.763 + (0.05916/2)log(0.05) = - 0.801V
Dal confronto dei valori dei potenziali si può ritenere che la reazione che ha luogo è:
Zn(s) + Cu2+ = Zn2+ + Cu(s)
Per cui l’espressione della f.e.m. è:
E = e(+)- e(-) = eCu- eZn
Andando a sostituire i valori numerici si ha:
IMPIEGO DEI POTENZIALI DI OSSIDO-RIDUZIONE
In riferimento ai potenziali di ossido-riduzione delle semicoppie, è possibile stabilire se un processo di ossido-riduzione assegnato è, oppure non, spontaneo.
Esempio:
Verificare se Al e Cu metallici, considerati separatamente, passano in soluzione trattandoli con una soluzione di HCl 1M, sapendo che e°(Al3+/Al) = - 1.50V, e°(Cu2+/Cu) = + 0.337V e che e°(H+/H2) = 0.000V.
Nel caso dell’alluminio, bisogna considerare le due semireazioni che combinate danno informazioni sulla spontaneità della reazione.
Considerando, infatti, le due semireazioni:
Al3+ + 3e = Al(s)
2H+ +2e = H2(g)
Combinandole opportunamente si avrà la reazione complessiva:
2Al(s) + 6H+ = 2Al3+ + 3H2(g)
In accordo ai valori di e°(Al3+/Al) e di e°(H+/H2) segue che:
e°(Al3+/Al)<e°(H+/H2) per cui la f.e.m. della cella è data come:
E = e(+)- e(-) = eH- eAl = 0 - (- 1.5) = + 1.5V
Dal punto di vista termodinamico, quindi, l’alluminio si scioglie in una soluzione di HCl 1M.
Nel caso del rame, bisogna considerare le due semireazioni che combinate danno informazioni sulla spontaneità della reazione.
Considerando, infatti, le due semireazioni:
Cu2+ + 2e = Cu(s)
2H+ +2e = H2(g)
Combinandole opportunamente si avrà la reazione complessiva:
Cu(s) + 2H+ = Cu2+ + H2(g)
In accordo ai valori di e°(Cu2+/Cu) e di e°(H+/H2) segue che:
e°(Cu2+/Cu)>e°(H+/H2) per cui la f.e.m. della cella è data come:
E = e(+)- e(-) = eH- eCu = 0 - (+ 0.337) = - 0.337V
Dal punto di vista termodinamico, quindi, il rame non si scioglie in una soluzione di HCl 1M, infatti la reazione spontanea è rappresentata dal fenomeno di riduzione del rame da una sua soluzione facendo gorgogliare idrogeno gassoso.
EQUILIBRI DI OSSIDO-RIDUZIONE IN ACQUA
RIDUZIONE DELL’ACQUA
Esempio:
Stabilire se l’alluminio metallico in acqua si scioglie sapendo che e°(Al3+/Al) = - 1.50V e che e°(H2O/H2) = - 0.413V.
In questo caso, bisogna considerare le due semireazioni che combinate danno informazioni sulla spontaneità della reazione.
Considerando, infatti, le due semireazioni:
Al3+ + 3e = Al(s)
2H2O +2e = H2(g) + 2OH-
Combinandole opportunamente si avrà la reazione complessiva:
2Al(s) + 6H2O = 2Al3+ + 3H2(g) + 6OH-
In accordo ai valori di e°(Al3+/Al) e di e°(H2O/H2) segue che:
e°(Al3+/Al)<e°(H2O/H2) per cui la f.e.m. della cella è data come:
E = e(+)- e(-) = eH2O- eAl = - 0.413 - (- 1.50) = + 1.09V
Dal punto di vista termodinamico, quindi, l’alluminio metallico si scioglie in H2O.
Sostanze con un potenziale di riduzione inferiore a – 0.413V si sciolgono in acqua provocando sviluppo di H2(g).
OSSIDAZIONE DELL’ACQUA
Per questo processo bisogna considerare la semireazione:
O2(g) + 4H+ + 4e = 2H2O e° = + 1.23V
Con discorsi analoghi a quelli fatti in precedenza segue che sostanze con un potenziale di riduzione superiore a + 1.23V provocano sviluppo di O2(g).
In molti casi, tuttavia, la reazione non avviene in quanto intervengono fattori cinetici, come l’eccessiva lentezza del processo, che richiedono, così, l’uso di un opportuno catalizzatore. Un caso è rappresentato dalle soluzioni di MnO4-.
Esempio:
Stabilire se una soluzione di Co(NO3)3 0.1M è stabile in acqua sapendo che e°(Co3+/Co2+) = + 1.82V e che e°(O2/H2O) = + 1.23V.
In questo caso, bisogna considerare le due semireazioni che combinate danno informazioni sulla spontaneità della reazione.
Considerando, infatti, le due semireazioni:
Co3+ + e = Co2+
O2(g) + 4H+ + 4e = 2H2O
Combinandole opportunamente si avrà la reazione complessiva:
4Co3+ + 2H2O = 4Co2+ + O2(g) + 4H+
In accordo ai valori di e°(Co3+/Co2+) e di e°(O2/H2O) segue che:
e°(Co3+/Co2+)>e°(O2/H2O) per cui la f.e.m. della cella è data come:
E = e(+)- e(-) = eCo- eH2O = + 1.82 - (+ 1.23) = + 0.59V
Dal punto di vista termodinamico, quindi, soluzioni di Co3+ non sono stabili in H2O e ciò è in accordo anche dal punto di vista cinetico. Le soluzioni di Co3+, infatti, “deteriorano” molto rapidamente.
Esempio:
Stabilire se una soluzione di FeSO4 1M è stabile in acqua sapendo che e°(Fe3+/Fe2+) = + 0.77V e che e°(O2/H2O) = + 1.23V.
In questo caso, bisogna considerare le due semireazioni che combinate danno informazioni sulla spontaneità della reazione.
Considerando, infatti, le due semireazioni:
Fe3+ + e = Fe2+
O2(g) + 4H+ + 4e = 2H2O
Combinandole opportunamente si avrà la reazione complessiva:
4Fe2+ + O2(g) + 4H+ = 4Fe3+ + 2H2O
In accordo ai valori di e°(Fe3+/Fe2+) e di e°(O2/H2O) segue che:
e°(Fe3+/Fe2+)<e°(O2/H2O) per cui la f.e.m. della cella è data come:
E = e(+)- e(-) = eH2O- eFe = + 1.23 - (+ 0.77) = + 0.46V
Dal punto di vista termodinamico, quindi, soluzioni di Fe2+ non sono stabili in H2O. Tuttavia in questo caso intervengono questioni cinetiche, che rallentano la reazione in maniera considerevole, rendendola possibile solo in presenza di opportuni catalizzatori.
DISSOLUZIONE DI METALLI CON ACIDI
Utilizzo di soluzioni di HCl:
Per queste soluzioni si fa riferimento alla semireazione:
H+ + e = (1/2)H2(g) e° = 0.00V
Semireazione di riduzione
|
e°,V |
Au3+ + 3e = Au(s) |
+ 1.50 |
Ag+ + e = Ag(s) |
+ 0.799 |
Hg22+ + 2e = Hg(l) |
+ 0.792 |
PtCl42- + 2e = Pt(s) + 4Cl- |
+ 0.73 |
Pd2+ + 2e = Pd(s) |
+ 0.623 |
Cu2+ + 2e = Cu(s) |
+ 0.337 |
BiO+ + 2H+ + 3e = Bi(s) + H2O |
+ 0.32 |
HAsO2 + 3H+ + 3e = As(s) + H2O |
+ 0.247 |
SbO+ + 2H+ + 3e = Sb(s) + H2O |
+ 0.212 |
H2MoO4 + 6H+ + 6e = Mo(s) + 4H2O |
0.00 |
Pb2+ + 2e = Pb(s) |
- 0.126 |
Sn2+ + 2e = Sn(s) |
- 0.14 |
Ni2+ + 2e = Ni(s) |
- 0.24 |
Co2+ + 2e = Co(s) |
- 0.277 |
Cd2+ + 2e = Cd(s) |
- 0.40 |
Fe2+ + 2e = Fe(s) |
- 0.44 |
Cr3+ + 3e = Cr(s) |
- 0.74 |
Zn2+ + 2e = Zn(s) |
- 0.763 |
Mn2+ + 2e = Mn(s) |
- 1.03 |
Al3+ + 3e = Al(s) |
- 1.50 |
Utilizzo di soluzioni di HNO3:
Per queste soluzioni si fa riferimento alla semireazione:
NO3- + 4H+ + 3e = NO(g) + 2H2O e° = + 0.96V
Le soluzioni di acido nitrico, dato il valore positivo di e°, vengono utilizzate come agenti ossidanti.
· Alcuni elementi trattati con soluzioni di acido nitrico formano specie acide.
Esempio:
3As(s) + 5NO3- + 5H+ = 3H3AsO4 + 5NO(g)
· Altri elementi, invece, formano degli ossidi insolubili dopo trattamento con acido nitrico.
Esempio:
3Sn(s) + 4NO3- + 4H+ = 3SnO2(s) + 4NO(g) + 2H2O
DISSOLUZIONE DI COMPOSTI POCO SOLUBILI
Una classe di composti poco solubili, i solfuri, possono essere disciolti se trattati con HNO3.
Esempio:
[Hg2+][S2-] = 10-52M2
[Ag+]2[S2-] = 10-49M3
[Fe2+][S2-] = 10-16M2
[Mn2+][S2-] = 10-12M2
La dissoluzione di questi solfuri può essere ottenuta ossidando, con soluzioni di HNO3 1M, lo ione S2-.
Se si considerano le due semireazioni:
S(s) + 2e = S2- e° = - 0.48V
NO3- + 4H+ + 3e = NO(g) + 2H2O e° = + 0.96V
si osserva, in accordo ai valori dei corrispondenti e°, che è possibile la ossidazione dello ione solfuro a zolfo con conseguente dissoluzione del precipitato.
Se si considera la reazione di ossido-riduzione:
aOx1 + bRed2 = bOx2 + aRed1
che si genera dalle due semireazioni:
Ox1 + n1e = Red1 e°1
Ox2 + n2e = Red2 e°2
si può dimostrare che la costante di equilibrio, a 25°C, si calcola mediante l’espressione:
logKeq = nE°/0.05916
dove n (an1 = bn2) rappresenta la condizione per cui il numero di elettroni ceduti dalla specie che si ossida è uguale al numero di elettroni acquistati dalla specie che si riduce garantendo, così, l’assenza di elettroni liberi in soluzione. La grandezza E° = e°1- e°2è valutata considerando che la prima semicoppia subisce il processo di riduzione mentre la seconda semicoppia subisce il processo di ossidazione in relazione a come viene scritta la reazione indipendentemente dai valori numerici degli e°.
E’ da ricordare, inoltre, che n corrisponde direttamente al prodotto di n1 e n2 solo se n1 e n2 non sono uno multiplo dell’altro. Diversamente n si identifica con il multiplo maggiore.
DIMOSTRAZIONE:
La reazione di ossido-riduzione:
aOx1 + bRed2 = bOx2 + aRed1
si genera dalle due semireazioni:
Ox1 + n1e = Red1
Ox2 + n2e = Red2
Applicando per ciascuna semicoppia l’equazione di Nernst, si ha:
e1 = e°1 + (0.05916/n1)log([Ox1]/[Red1])
e2 = e°2 + (0.05916/n2)log([Ox2]/[Red2])
Sottraendo membro a membro si ha:
e1- e2 = e°1- e°2 +
(0.05916/n1)log([Ox1]/[Red1]) - (0.05916/n2)log([Ox2]/[Red2])
All’equilibrio DG = nFE = 0, che è vero quando E = e1- e2 = 0 segue che e1 = e2, per cui l’equazione scritta in precedenza assume la forma:
0 = e°1- e°2 +
(0.05916/n1)log([Ox1]/[Red1]) - (0.05916/n2)log([Ox2]/[Red2])
Per eseguire la differenza tra i logaritmi è necessario che siano uguali i loro coefficienti; quindi se indichiamo con a e b rispettivamente i valori per cui an1 = bn2 si ha:
0 = e°1- e°2 +
(0.05916/n1)(a/a)log([Ox1]/[Red1]) - (0.05916/n2)(b/b)log([Ox2]/[Red2])
Svolgendo l’espressione si ha:
0 = e°1- e°2 +
(0.05916/n1a)log([Ox1]a/[Red1]a) - (0.05916/n2b)log([Ox2]b/[Red2]b)
A questo punto ponendo an1 = bn2 = n, e considerando il tutto come argomento in un solo logaritmo si ha:
0 = e°1- e°2 +
(0.05916/n)log(([Ox1]a/[Red1]a)/([Ox2]b/[Red2]b))
Portando al I° membro la differenza dei potenziali e avendo ammesso, in accordo all’equazione di equilibrio, che la specie 1 nel passare dai reagenti ai prodotti subisce la riduzione mentre la specie 2 subisce la ossidazione si ha:
e°1- e°2 = (0.05916/n)log(([Ox2]b/[Red2]b)/([Ox1]a/[Red1]a))
La quantità presente nell’argomento del logaritmo rappresenta la costante di equilibrio della reazione considerata, per cui si ottiene:
E° = e°1- e°2 = (0.05916/n)logKeq
Alla fine si ha:
logKeq = nE°/0.05916
Dall’espressione ottenuta si evince che:
· Quanto più l’e° della specie ossidante è differente dall’e° della specie riducente, tanto più il valore della costante di equilibrio è elevato.
· Sul valore numerico della costante influisce anche n, ciò si traduce col dire che quanto più le specie reagenti nel passare ai prodotti cambiano il loro stato di ossidazione tanto più il valore della costante è elevato.
Esempio:
Calcolare la costante di equilibrio per la reazione:
2Ce4+ + Sn2+ = 2Ce3+ + Sn4+
sapendo che e°(Ce4+/Ce3+) = + 1.61V e e°(Sn4+/Sn2+) = + 0.15V.
La reazione considerata prende origine dall’accoppiamento delle due semireazioni:
Ce4+ + e = Ce3+ e°1 = + 1.61V
Sn4+ + 2e = Sn2+ e°2 = + 0.15V
All’equilibrio DG = nFE = 0, che è vero quando E = eCe- eSn = 0 segue che eCe = eSn.
Applicando per ciascun semielemento l’equazione di Nernst, si ha:
e°Ce + (0.05916/1)log([Ce4+]/[Ce3+]) =
e°Sn + (0.05916/2)log([Sn4+]/[Sn2+])
da cui:
e°Ce + (0.05916/1)(2/2)log([Ce4+]/[Ce3+]) =
e°Sn + (0.05916/2)log([Sn4+]/[Sn2+])
e°Ce + (0.05916/2)log([Ce4+]2/[Ce3+]2) =
e°Sn + (0.05916/2)log([Sn4+]/[Sn2+])
Sottraendo membro a membro e semplificando, si ha:
e°Ce- e°Sn = (0.05916/2)log([Ce3+]2[Sn4+]/[Sn2+][Ce4+]2) = logKeq
da cui segue in questo caso particolare:
logKeq = 2(e°Ce- e°Sn)/0.05916
andando a sostituire si ha:
logKeq = 2(1.61 - 0.15)/0.05916 = 49.36
Come si osserva, dal valore numerico della costante, la reazione può essere sfruttata per scopi analitici in quanto la conversione dei reagenti nei prodotti è praticamente quantitativa.
Esempio:
Calcolare la costante di equilibrio per la reazione:
2Al(s) + Cr2O72- + 14H+ = 2Al3+ + 2Cr3+ + 7H2O
sapendo che e°(Cr2O72-/Cr3+) = + 1.33V e e°(Al3+/Al) = - 1.50V.
La reazione considerata prende origine dall’accoppiamento delle due semireazioni:
Cr2O72- + 6e + 14H+ = 2Cr3+ + 7H2O e°1 = + 1.33V
Al3+ + 3e = Al(s) e°2 = - 1.50V
All’equilibrio DG = nFE = 0, che è vero quando E = eCr2O7- eAl = 0 segue che eCr2O7 = eAl.
Applicando per ciascun semielemento l’equazione di Nernst, si ha:
e°Cr2O7 + (0.05916/6)log([Cr2O72-][H+]14/[Cr3+]2) =
e°Al + (0.05916/3)log([Al3+])
da cui:
e°Cr2O7 + (0.05916/6)log([Cr2O72-][H+]14/[Cr3+]2) =
e°Al + (0.05916/3)(2/2)log([Al3+])
e°Cr2O7 + (0.05916/6)log([Cr2O72-][H+]14/[Cr3+]2) =
e°Al + (0.05916/6)log([Al3+]2)
Sottraendo membro a membro e semplificando, si ha:
e°Cr2O7- e°Al = (0.05916/6)log([Cr3+]2[Al3+]2/[Cr2O72-][H+]14) = logKeq
da cui segue in questo caso particolare:
logKeq = 6(e°Cr2O7- e°Al)/0.05916
andando a sostituire si ha:
logKeq = 6(1.33 + 1.50)/0.05916 = 287.01
Come si osserva, dal valore della costante, la reazione può essere sfruttata per scopi analitici in quanto la conversione dei reagenti nei prodotti è praticamente quantitativa.
Esempio:
Calcolare la costante di equilibrio per la reazione:
2MnO4- + 5C2O42- + 16H+ = 2Mn2+ + 10CO2(g) + 8H2O
sapendo che e°(MnO4-/Mn2+) = + 1.49V e e°(CO2/C2O42-) = - 0.50V.
La reazione considerata prende origine dall’accoppiamento delle due semireazioni:
MnO4- + 5e + 8H+ = Mn2+ + 4H2O e°1 = + 1.49V
2CO2(g) + 2e = C2O42- e°2 = - 0.50V
All’equilibrio DG = nFE = 0, che è vero quando E = eMnO4- eCO2 = 0 segue che eMnO4 = eCO2.
Applicando per ciascun semielemento l’equazione di Nernst, si ha:
e°MnO4 + (0.05916/5)log([MnO4-][H+]8/[Mn2+]) =
e°CO2 + (0.05916/2)log(p(CO2)2/[C2O42-])
da cui:
e°MnO4 + (0.05916/5)(2/2)log([MnO4-][H+]8/[Mn2+]) =
e°CO2 + (0.05916/2)(5/5)log(p(CO2)2/[C2O42-])
e°MnO4 + (0.05916/10)log([MnO4-]2[H+]16/[Mn2+]2) =
e°CO2 + (0.05916/10)log(p(CO2)10/[C2O42-]5)
Sottraendo membro a membro e semplificando, si ha:
e°MnO4- e°CO2 = (0.05916/10)log([Mn2+]2p(CO2)10/[MnO4-]2[H+]16[C2O42-]5) = logKeq
da cui segue in questo caso particolare:
logKeq = 10(e°MnO4- e°CO2)/0.05916
andando a sostituire si ha:
logKeq = 10(1.49 + 0.50)/0.05916 = 336.38
Come si osserva, dal valore della costante, la reazione può essere sfruttata per scopi analitici in quanto la conversione dei reagenti nei prodotti è praticamente quantitativa.
In particolare poiché la reazione ha luogo in ambiente acido, per H2SO4, più correttamente la reazione va scritta e bilanciata non considerando la specie C2O42-, che prevale in ambiente “più alcalino” di quello garantito dalla soluzione di acido solforico, bensì la specie H2C2O4 che è quella che prevale nelle condizioni sperimentali.
Quindi in accordo a ciò si ha:
2MnO4- + 5H2C2O4 + 6H+ = 2Mn2+ + 10CO2(g) + 8H2O
Esempio:
Calcolare la costante di equilibrio per la reazione:
Au(s) + NO3- + 4H+ = Au3+ + NO(g) + 2H2O
sapendo che e°(Au3+/Au) = + 1.50V e e°(NO3-/NO) = + 0.96V.
La reazione considerata prende origine dall’accoppiamento delle due semireazioni:
NO3- + 3e + 4H+ = NO(g) + 2H2O e°1 = + 0.96V
Au3+ + 3e = Au(s) e°2 = + 1.50V
All’equilibrio DG = nFE = 0, che è vero quando E = eNO3- eAu = 0 segue che eNO3 = eAu.
Applicando per ciascun semielemento l’equazione di Nernst, si ha:
e°NO3 + (0.05916/3)log([NO3-][H+]4/p(NO)) =
e°Au + (0.05916/3)log([Au3+])
Sottraendo membro a membro e semplificando, si ha:
e°NO3- e°Au = (0.05916/3)log([Au3+]p(NO)/[NO3-][H+]4) = logKeq
da cui segue, in questo caso particolare:
logKeq = 3(e°NO3- e°Au)/0.05916
andando a sostituire si ha:
logKeq = 3(0.96 - 1.50)/0.05916 = - 27.38
Come si osserva, dal valore negativo della costante, la reazione non può essere sfruttata per scopi analitici in quanto la conversione dei reagenti nei prodotti non è quantitativa. Solo una piccola parte si converte, favorendo, così, la reazione inversa.
Alcune reazioni di ossido-riduzione possono essere utilizzate per la determinazione di sostanze incognite presenti in campioni da analizzare.
In genere il titolante è rappresentato da un ossidante energico, in quanto l’impiego di riducenti come titolanti porterebbe come inconveniente la loro esposizione ad O2 atmosferico.
PUNTO EQUIVALENTE
Il punto equivalente in una titolazione di ossido-riduzione si ha quando si raggiunge l’uguaglianza tra gli equivalenti di titolante aggiunti e gli equivalenti del titolando presenti nel campione.
Se la semicoppia 1 è quella rappresentata dal titolante a cui compete la semireazione:
Ox1 + n1e = Red1
mentre la semicoppia 2 è quella rappresentata dal titolando a cui compete la semireazione:
Ox2 + n2e = Red2
e indicando, inoltre, con CT la concentrazione, molare, del titolante, Ox1, e con C la concentrazione, molare, del titolando Red2; al punto equivalente si avrà:
n1CT = n2C
(le concentrazioni si riferiscono al punto finale della titolazione).
Esempio:
Valutare il punto finale della titolazione di Sn2+ con Ce4+, sapendo che e°(Ce4+/Ce3+) = + 1.61V e e°(Sn4+/Sn2+) = + 0.15V.
In accordo ai valori di e° segue che il titolante è rappresentato dalla soluzione di Ce4+ mentre il titolando è rappresentato dalla soluzione di Sn2+.
La reazione da considerare, bilanciata, è:
2Ce4+ + Sn2+ = 2Ce3+ + Sn4+
che prende origine dalle semireazioni:
Ce4+ + e = Ce3+
Sn4+ + 2e = Sn2+
Al p.e. risulta:
CCe = 2CSn
CURVA DI TITOLAZIONE PER REAZIONI DI OSSIDO-RIDUZIONE
Per questo tipo di titolazione, si riporta la variazione di potenziale della soluzione in funzione del volume di titolante aggiunto.
E’ da ricordare che in dipendenza del volume di titolante aggiunto, prima di arrivare al punto equivalente la semicoppia che definisce il potenziale della soluzione è rappresentata dal titolando in quanto in soluzione è presente sia la forma ossidata che la forma ridotta. Dopo il punto equivalente, ovviamente, a definire il potenziale della soluzione sarà la semicoppia del titolante in quanto in soluzione sarà presente sia la forma ossidata che la forma ridotta.
Se in una soluzione è presente solo la forma ossidata o solo la forma ridotta di una semicoppia di ossido-riduzione, l’equazione di Nernst non può essere applicata.
Consideriamo, per esempio, una soluzione di Fe2+ come titolando di volume iniziale V0 e concentrazione iniziale C0, e ad essa si aggiungono volumi crescenti, VT, di titolante a concentrazione iniziale C0T, per esempio, di una soluzione di Ce4+. Tra il titolante aggiunto e il titolando ha luogo la reazione:
Ce4+ + Fe2+= Fe3+ + Ce3+
dove e°T = e°Ce = + 1.61V
e° = e°Fe = + 0.77V
Per un generico punto della titolazione:
CFe = [Fe2+] + [Fe3+] = C0V0/VTOT
CCe = [Ce3+] + [Ce4+] = C0TVT/VTOT
Ponendo, ad esempio, V0 = 50cm3, C0 = 0.1M e C0T = 0.1M, si costruisce la curva di titolazione riportando il potenziale “e” dell’opportuna semicoppia in funzione del volume VT, oppure della frazione titolata
f = CT/C = C0TVT/C0V0 (in generale f = nTCT/nC = nTC0TVT/nC0V0).
Dalla stechiometria della reazione, in un punto generico della titolazione, è sempre vero:
[Ce3+] = [Fe3+]
Prima del p.e.:
CCe = [Ce3+] = C0TVT/VTOT = [Fe3+]
[Fe2+] = CFe- [Fe3+] = (C0V0- C0TVT)/VTOT
Prima del punto equivalente la semicoppia che definisce il valore del potenziale è quella riferita al titolando per cui applicando l’equazione di Nernst si ha:
e = e° + 0.05916log([Fe3+]/[Fe2+]) =
e° + 0.05916log((C0V0- C0TVT)/C0TVT)
Es.: aggiunta di VT = 20cm3 f = 0.4 e = 0.760V
aggiunta di VT = 49cm3 f = 0.98 e = 0.87V
Al p.e. per un processo generico:
OxT + Red = RedT + Ox
il potenziale si calcola mediante l’equazione:
epe = (nTe°T + ne°)/(nT + n)
DIMOSTRAZIONE:
La reazione di ossido-riduzione:
OxT + Red = Ox + RedT
si genera dalle due semireazioni:
OxT + nTe = RedT
Ox + ne = Red
Sfruttando la condizione dell’elettrone secondo cui gli elettroni ceduti dal titolando (titolato) sono uguali a quelli acquistati dal titolante si ha:
Forme redox di partenza: Red, OxT
Cessione di elettroni: Red = Ox + n2e
Acquisto di elettroni: OxT + n1e = RedT
In altri termini la condizione dell’elettrone può essere riassunta nella forma:
n[Red] = nT[OxT]
Poiché al punto equivalente è vero che:
nTCT = nC
andando a sostituire al posto di CT e C rispettivamente la somma della concentrazione della specie ossidata e della specie ridotta, si può ricavare:
n[Ox] = nT[RedT]
Per cui è possibile sempre scrivere:
n[Red] = nT[OxT]
n[Ox] = nT[RedT]
Applicando per ciascuna semicoppia l’equazione di Nernst, si ha:
eT = e°T + (0.05916/nT)log([OxT]/[RedT])
e = e° + (0.05916/n)log([Ox]/[Red])
Moltiplicando entrambi i membri delle due equazioni per il numero degli elettroni si ha:
nTeT = nTe°T + (0.05916)log([OxT]/[RedT])
ne = ne° + (0.05916)log([Ox]/[Red])
Sommando membro a membro si ha:
nTeT + ne = nTe°T + ne° +
(0.05916)log([OxT]/[RedT]) + (0.05916)log([Ox]/[Red])
Al punto equivalente i potenziali delle due semicelle sono uguali in quanto non c’è più passaggio di corrente per cui epe = eT = e, così l’equazione scritta in precedenza assume la forma:
(nT + n)epe = nTe°T + ne° +
(0.05916)log(([OxT]/[RedT])([Ox]/[Red]))
Ricordando dalle relazioni precedenti che:
[OxT]/[Red] = n/nTe [Ox]/[RedT] = nT/n
l’argomento del logaritmo è 1 quindi si perviene al risultato:
epe = (nTe°T + ne°)/(nT + n)
L’equazione ottenuta non è di validità generale, in quanto è applicabile solo per i sistemi le cui semireazioni non contengono né specie polinucleari, né ioni H+ oppure ioni OH-.
Quindi per il sistema Ce-Fe il potenziale al punto equivalente vale:
epe = + 1.19V
Laddove, nel bilanciamento, ci fosse bisogno di specie come H+ oppure OH- l’espressione del potenziale al punto equivalente assume l’espressione:
epe = ((nTe°T + ne°) + (0.05916log[H+]a))/(nT + n)
epe = ((nTe°T + ne°) + (0.05916log[OH-]a))/(nT + n)
Il parametro a è l’esponente numerico relativo alla specie H+ oppure OH- che si ricava dalle due semireazioni.
Se, ad esempio, la specie H+ oppure OH- è coinvolta in entrambe le due semireazioni e, in particolare, compare, per entrambe le semireazioni, dal lato della forma ossidata del titolante e del titolato, i coefficienti si sommano, diversamente se compaiono da lati opposti. Ai fini della somma algebrica, l’esponente è preso col segno positivo se si trova dal lato della forma ossidata e col segno meno se si trova dal lato della forma ridotta.
Dopo il p.e.:
[Ce3+] = [Fe3+] = CFe = C0TVT/VTOT
[Ce4+] = CCe- [Ce3+] = (C0TVT- C0V0)/VTOT
Dopo il punto equivalente la semicoppia che definisce il valore del potenziale è quella riferita al titolante per cui applicando l’equazione di Nernst si ha:
e = e°T + 0.05916log([Ce4+]/[Ce3+]) =
e°T + 0.05916log((C0TVT- C0V0)/C0TVT)
In questa classe di titolazioni, il punto di equivalenza coincide con il punto di massima pendenza della curva (punto di flesso).
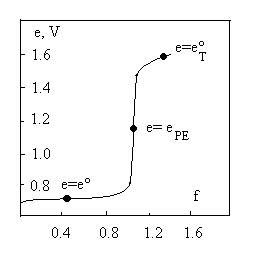
CALCOLO DEL POTENZIALE AL PUNTO EQUIVALENTE
Esempio:
Scrivere l’espressione e valutare il potenziale al p.e. per la titolazione di Sn2+ con Ce4+, sapendo che e°(Ce4+/Ce3+) = + 1.61V e e°(Sn4+/Sn2+) = + 0.15V.
La reazione alla base della titolazione, bilanciata, è:
2Ce4+ + Sn2+ = 2Ce3+ + Sn4+
In base a quanto visto prima si ha:
epe = e°(Ce4+/Ce3+) + 2e°(Sn4+/Sn2+)/(1 + 2) =
(+ 1.61 + 2(+ 0.15))/3 = + 0.64V
Esempio:
Scrivere l’espressione e valutare il potenziale al p.e. per la titolazione del Tl+ con MnO4- in H2SO4 1M sapendo che e°(MnO4-/Mn2+) = + 1.49V e e°(Tl3+/Tl+) = + 1.25V.
La reazione alla base della titolazione, bilanciata, è:
2MnO4- + 5Tl+ + 16H+ = 2Mn2+ + 5Tl3+ + 8H2O
In questo caso per bilanciare la semireazione dello ione permanganato, viene coinvolto anche lo ione H+. L’espressione del potenziale al punto equivalente dipende, quindi, anche dal termine della concentrazione idrogenionica. L’esponente è uguale al coefficiente dello ione H+ richiesto per bilanciare la semireazione dello ione permanganato. Così per questa reazione l’espressione del potenziale al punto equivalente è:
epe = (5e°(MnO4-/Mn2+) + 2e°(Tl3+/Tl+) + 0.05916log([H+])8)/(5 + 2) =
(5(+ 1.49) + 2(+ 1.25))/7 = + 1.42V
INDICATORI DI OSSIDO-RIDUZIONE
E’ un sistema di ossido-riduzione la cui forma ossidata ha una colorazione differente dalla forma ridotta. In analogia agli indicatori acido-base, si definisce un intervallo di potenziale in cui avviene la variazione di colore (intervallo di viraggio).
Si può, quindi, scrivere per l’indicatore il seguente equilibrio di ossido-riduzione:
In(Ox) + ne = In(Red)
a cui si associa l’equazione di Nernst:
e = e°In + (0.05916/n)log([In(Ox)]/[In(Red)])
il colore della forma In(Ox) predomina quando [In(Ox)]/[In(Red)]>10
il colore della forma In(Red) predomina quando [In(Ox)]/[In(Red)]<0.1
quindi l’intervallo di viraggio si ha quando:
e = e°In± 0.05916/n
Una volta calcolato il potenziale al punto equivalente (epe), l’indicatore si sceglie in modo tale che:
epe = e°In± 0.05916/n
Indicatori di ossido-riduzione
Indicatore |
Colore forma ossidata |
Colore forma ridotta |
e°In,V
|
Nitroferroina (1) |
blu tenue |
Rosso |
1.25 |
Ferroina(2) |
blu tenue |
Rosso |
1.06 |
Fe(II) –2,2’-bipiridile |
blu |
Rosso |
1.02 |
5,6-dimetilferroina |
blu tenue |
Rosso |
0.97 |
Acido N-fenilantranilico |
rosso |
Incolore |
0.89 |
4,7-dimetilferroina |
blu tenue |
Rosso |
0.88 |
Acido difenilamminosolfonico |
rosso-viola |
Incolore |
0.85 |
Difenilbenzidina |
violetto |
Incolore |
0.76 |
Difenilammina |
violetto |
Incolore |
0.76 |
3,3’-dimetilnaftidina |
rosso-porpora |
Incolore |
0.71 |
Amido iodurato, KI |
blu |
Incolore |
0.53 |
Blu di metilene |
blu |
Incolore |
0.52 |
Fenosafranina |
rosso |
Incolore |
0.28 |
(1): (Fe(II)-5-nitro-1,10-fenantrolina); (2): (Fe(II)-1,10-fenantrolina)
Gli indicatori di ossido-riduzione più importanti sono la difenilammina e la ferroina. La ferroina è un complesso tra Fe2+ e 3 molecole di 1,10-fenantrolina. Il Fe2+ si ossida a Fe3+ in accordo alla reazione:
[Fe(C12H8N2)3]3+ + e = [Fe(C12H8N2)3]2+ e°In = + 1.06V
In base alla più intensa colorazione, quella della forma ridotta, il viraggio diventa percettibile quando il potenziale è intorno a + 1.12V e non per un valore uguale a e°In.
REAGENTI CHE FUNGONO DA INDICATORI
Alcuni reattivi sono intensamente colorati per cui loro stessi se presenti in eccesso oppure la loro scomparsa comporta una variazione di colore, quindi possono essere sfruttati come punto di arresto della titolazione.
Un esempio è rappresentato dalle soluzioni di KMnO4, reagente molto usato nelle titolazioni che fanno uso di agenti ossidanti. La forma ossidata è intensamente colorata in viola anche se è presente in concentrazioni dell’ordine di 10-5M.
Altro esempio è rappresentato da I2. Lo iodio messo in libertà dalla reazione si può estrarre in CHCl3 oppure in CCl4, impartendo alla fase organica una colorazione viola. Ciò nonostante per questo tipo di reazione si utilizza la salda d’amido come indicatore capace di rilevare anche piccole tracce di I2 in un campione.
Altro esempio è rappresentato dallo ione Fe2+ nelle titolazioni dove viene ossidato a Fe3+. E’ possibile usare come ione indicatore la specie SCN-, che forma con lo ione Fe3+ un complesso intensamente colorato in rosso di formula FeSCN2+.
Si definiscono tali tutti quei metodi di ossido-riduzione dove la sostanza da determinare in un campione viene ossidata a carico di un agente ossidante.
Principali agenti ossidanti utilizzati nelle titolazioni:
(NH4)2Ce(SO4)3 (solfato di cerio(IV) e ammonio)
KMnO4 (permanganato di potassio)
K2Cr2O7 (dicromato di potassio)
Coppia I2/I- (iodio/ioduro)
KIO3 (iodato di potassio)
KBrO3 (bromato di potassio)
Altre sostanze come HNO3, Cl2 e H2O2 non vengono impiegate in quanto o non sono sufficientemente stabili o le relative reazioni non decorrono secondo un unico e definito rapporto stechiometrico.
IMPIEGO DI Ce(IV) (CERIMETRIA)
Questa classe di titolazioni sfrutta la semireazione di ossido-riduzione:
Ce4+ + e = Ce3+ e° = + 1.43V (in H2SO4 1M)
Il reattivo titolante si ottiene a partire da (NH4)2Ce(SO4)3 oppure da (NH4)2Ce(NO3)6(s), sciolto in H2SO4 1M, l’ambiente acido evita la precipitazione dell’idrossido di cerio.
Si possono effettuare titolazioni in presenza di HCl (tranne per le titolazioni che necessitano di far bollire la soluzione, infatti in queste condizioni il cerio ossida Cl- a Cl2).
Un inconveniente dei sali di Ce(IV) è quello che non sono sostanze madri.
Standard primari utilizzati in Cerimetria:
As2O3 (PM = 197.84g/mol);
Na2C2O4 (PM = 134.00g/mol);
Fe (PA = 55.847g/mol);
Esempi di applicazioni della Cerimetria
· Dosaggio di metalli: Fe(II), Sn(II), ecc;
· Dosaggio degli ossalati (C2O42-);
· Dosaggio dei nitriti:
2Ce4+ + NO2- + H2O = 2Ce3+ + NO3- + 2H+
· Dosaggio dell’acqua ossigenata:
2Ce4+ + H2O2 = 2Ce3+ + O2(g) + 2H+
IMPIEGO DI KMnO4 (PERMANGANOMETRIA)
Tra i metodi in ossidazione rappresenta il più diffuso in chimica analitica.
Le reazioni portano a prodotti differenti in base alle condizioni sperimentali utilizzate.
· In ambiente acido, per H2SO4 o HClO4 ma non per HNO3, è un forte ossidante e la semireazione di ossido-riduzione alla base del processo è:
MnO4- + 5e + 8H+ = Mn2+ + 4H2O e0 = + 1.49V
(PE = PM/5)
· In ambiente neutro o leggermente alcalino è ancora più ossidante e la semireazione di ossido-riduzione alla base del processo è:
MnO4- + 3e + 2H2O = MnO2 + 4OH- e° = + 1.695V
(PE = PM/3)
· In ambiente neutro è un blando ossidante e la semireazione di ossido-riduzione alla base del processo è:
MnO4- + e = MnO42- e° = + 0.564V
(PE = PM)
La principale applicazione delle soluzioni di KMnO4 è quella in soluzione acida per H2SO4, in concentrazione 1 - 5M. Si preferisce l’acido solforico in quanto l’anione solfato non mostra né proprietà di complessazione né presenta proprietà di ossido-riduzione.
Si sconsiglia l’uso di HCl in quanto può reagire, in presenza di alcune sostanze come Fe2+. La determinazione di As(III), Sb(III) e H2O2 si può effettuare, invece, in presenza di HCl.
Lo ione MnO4-, è colorato in violetto, mentre il prodotto di riduzione in ambiente acido, Mn2+, è incolore, il titolante, quindi, ha anche la funzione di indicatore.
Un inconveniente di KMnO4 è quello di non essere una sostanza madre.
Standard primari utilizzati in Permanganometria:
As2O3 (PM = 197.84g/mol);
Na2C2O4 (PM = 134.00g/mol);
Fe (PA = 55.847g/mol);
H2C2O4´2H2O (PM = 126.07g/mol);
K2Cr2O7 (PM = 294.19g/mol);
KIO3 (PM = 214.00g/mol);
Esempi di applicazioni della Permanganometria
· Dosaggio dell’acqua ossigenata:
2MnO4- + 5H2O2 + 6H+ = 2Mn2+ + 5O2(g) + 8H2O
· Dosaggio dei nitriti:
2MnO4- + 5NO2- + 6H+ = 2Mn2+ + 5NO3- + 3H2O
· Dosaggio di bromuri e ioduri:
2MnO4- + 10Br- + 16H+ = 2Mn2+ + 5Br2 + 8H2O
2MnO4- + 10I- + 16H+ = 2Mn2+ + 5I2 + 8H2O
· Dosaggio dello ione ossalato:
2MnO4- + 5H2C2O4 + 6H+ = 2Mn2+ + 10CO2(g) + 8H2O
· Dosaggio del calcio:
Precipitato come Ca2C2O4(s) e poi solubilizzato in H2SO4
· Dosaggio del ferro(II):
MnO4- + 5Fe2+ + 8H+ = Mn2+ + 5Fe3+ + 4H2O
IMPIEGO DI K2Cr2O7
Il dicromato di potassio viene utilizzato in ambiente acido per HCl (<2M), H2SO4 o HClO4.
La semireazione di ossido-riduzione alla base del processo è:
Cr2O72- + 6e + 14H+ = 2Cr3+ + 7H2O e0 = + 1.33V
(PE = PM/6)
Il dicromato di potassio è una sostanza madre; questo è un vantaggio che si ha preparando le soluzioni e utilizzandole come sostanze ossidanti.
Esempi di applicazioni con K2Cr2O7
· Dosaggio del ferro(II):
Cr2O72- + 6Fe2+ + 14H+ = 2Cr3+ + 6Fe3+ + 7H2O
· Dosaggio del COD:
Il COD (Chemical Oxigen Demand = richiesta di ossigeno chimico), corrisponde al contenuto di sostanza organica (indicata genericamente come (CH2O)n) presente in un’acqua di scarico, ossidabile chimicamente con K2Cr2O7 a caldo.
Si effettua sulle acque reflue prelevando un volume V0 (es. 50cm3) introducendolo in una beuta ed aggiungendo 1g di HgSO4(s) che favorisce la precipitazione di Cl-. Si aggiunge, con una pipetta tarata, un volume noto VT (es. 10cm3) di una soluzione di K2Cr2O7 di normalità nota NT (es. 0.25N) e il tutto viene completato con un refrigerante a ricadere.
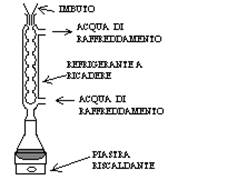
Si versa dall’alto, con un imbuto, circa 30cm3 di una soluzione allo 0.5% di AgNO3 in H2SO4 concentrato che funge da catalizzatore della reazione di ossidazione. Si fa bollire la soluzione per 2 ore.
La reazione alla base del processo è:
(6/n)(CH2O)n + 4Cr2O72- + 32H+ = 6CO2 + 8Cr3+ + 22H2O
Si raffredda la soluzione e si titola l’eccesso di K2Cr2O7, quantità che non ha reagito con la sostanza organica presente nel campione di acqua reflua, con una soluzione di FeSO4 (o di (NH4)2Fe(SO4)2) di normalità nota NFe (es.0.025N), usando come indicatore la ferroina. L’aggiunta della soluzione di Fe2+ si arresta quando l’indicatore vira dal blu tenue al rosso.
La reazione alla base del processo è:
Cr2O72- + 6Fe2+ + 14H+ = 2Cr3+ + 6Fe3+ + 7H2O
Gli equivalenti per litro (eq/l) di sostanza organica, (S.O.) presenti nel campione di acqua si ottengono dall’espressione:
S.O.(eq/l) = ((NTVT- NFeVFe)/V0)´1000
Il contenuto di sostanza organica si può anche esprimere come mg/l di O2 consumati per l’ossidazione, tramite la formula:
S.O.(mg/l O2) = S.O.(eq/l)´8.0´1000
L’espressione precedente si ottiene prendendo come sostanza organica di riferimento il biftalato di potassio (C6H4(COO)2HK) (PM = 204.22g/mol).
Infatti in accordo alla reazione di ossidazione, si ha:
C6H4(COO)2H- + (15/2)O2 + H+ = 8CO2 + 3H2O
Dalla reazione segue che:
moli(O2) = (15/2)moli di biftalato 1g di biftalato = 1.176g di O2
La semireazione di ossido-riduzione alla base di entrambi i metodi è:
(1/2)I2(aq) + e = I- e° = + 0.536V
Poiché il valore di e° è intermedio tra le sostanze ossidanti (alti valori di e°) e le sostanze riducenti (bassi valori di e°), è possibile utilizzare la semireazione sia nel senso dell’ossidazione che nel senso della riduzione.
IODIMETRIA
· Impiego di soluzioni di I2 come agente ossidante
(Iodimetria = metodo diretto):
La soluzione titolante è costituita da una soluzione di iodio.
I2(s) è una sostanza poco solubile in acqua (1.33´10-3M, a 25°C). In presenza di I- la solubilità dello iodio aumenta per la formazione del complesso I3- in accordo alla reazione:
I2(aq) + I- = I3-
E’ possibile preparare una soluzione 0.05M di I3-, sciogliendo 0.12mol di KI e 0.05mol di I2(s) in 1dm3 di acqua. Poiché I2(s) evapora facilmente non è, quindi, una sostanza madre quindi si prepara una soluzione a titolo approssimato e poi si passa a determinare il titolo della soluzione.
Standard primari utilizzati in Iodimetria:
As2O3 (PM = 197.84g/mol);
Na2S2O3´5H2O (PM = 248.18g/mol);
E’ possibile preparare una soluzione a titolo noto di iodio, pesando una quantità nota di KIO3 e di KI in eccesso. Con l’aggiunta di acido, per esempio HCl, ha luogo la reazione:
IO3- + 8I- + 6H+ = 3I3- + 3H2O
Esempi di applicazioni della Iodimetria
2Mn2+ + 4OH- + (1/2)O2(g) = 2MnOOH(s) + H2O
Successivamente si acidifica con HCl e si aggiunge un eccesso di KI formandosi I2 in accordo alla reazione:
2MnOOH(s) + 6H+ + 2I- = 2Mn2+ + I2 + 4H2O
Lo iodio messo in libertà si titola con una soluzione di Na2S2O3 a titolo noto.
· Dosaggio di stagno(II):
Sn2+ + I3- = Sn4+ + 3I-
Consente il dosaggio, in un campione di acqua, delle sostanze di natura organica (grassi, oli, ecc.).
Tale metodo riveste importanza quando non è possibile riscaldare il campione sottoposto all’analisi in quanto la sostanza da determinare, a seguito del riscaldamento, potrebbe decomporsi.
Il reagente, definito di Karl Fischer, è rappresentato da:
I2(s), piridina (C6H5N) e SO2(g) in metanolo nei rapporti 1:10:3.
In presenza di acqua avrà luogo la reazione:
SO2 + I2 + H2O ® SO3 + 2HI
Gli acidi che si formano vengono neutralizzati dalla piridina, con formazione della specie C5H5NH+SO3-.
Procedura: Un volume noto di campione in esame viene titolato con il reagente di Karl Fischer. Fino a quando vi è acqua lo iodio, in accordo alla reazione precedente, viene consumato. Al punto finale rimane un eccesso di I2 che colora la salda d’amido. Per soluzioni incognite colorate, il punto finale viene individuato con metodi strumentali.
· Impiego di soluzioni di I- come agente riducente
(Iodometria = metodo indiretto):
Per questo tipo di reazione, il principale problema è legato alla elevata volatilità di I2 che liberandosi nella reazione potrebbe allontanarsi dall’ambiente falsando così la determinazione. Si ovvia a questo inconveniente lavorando in eccesso di I- che forma con I2 la specie I3- stabile in soluzione. La sostanza da determinare reagisce con I-.
Lo iodio messo in libertà viene titolato con una soluzione di Na2S2O3 in accordo alla reazione:
I3- + 2S2O32- = 3I- + S4O62-
Il tiosolfato di sodio è una sostanza deliquescente e inoltre il contenuto di molecole di acqua presente nel sale è variabile quindi non è uno standard primario. Si prepara, quindi, una soluzione a titolo approssimato dal sale rappresentato da Na2S2O3´5H2O e si determina il titolo impiegando un opportuno standard primario.
Standard primari utilizzati in Iodometria:
As2O3 (PM = 197.84g/mol);
K2Cr2O7 (PM = 294.20g/mol);
KIO3 (PM = 214.00g/mol);
L’impiego di tale sistema è particolarmente diffuso per la disponibilità di un indicatore visuale, la salda d’amido. L’amido, polisaccaride naturale di struttura elicoidale, interagisce con I2 assumendo una colorazione azzurra. La reazione è reversibile ed è particolarmente sensibile anche a tracce di I2.
La presenza di I2 o la sua scomparsa da soluzioni è reso molto sensibile da questo sistema di rivelazione.
Esempi di applicazioni della Iodometria
· Dosaggio del biossido di manganese(IV):
MnO2 + 4H+ + 2Cl- = Mn2+ + Cl2 + 2H2O
Cl2 + 2I- = 2Cl- + I2
· Dosaggio del rame(II):
2Cu2+ + 4I- = 2CuI(s) + I2
· Dosaggio del cloro “attivo” negli ipocloriti:
OCl- + 2I- + 2H+ = Cl- + I2 + H2O
· Dosaggio dell’acqua ossigenata:
H2O2 + 2H+ + 2I- = I2 + 2H2O
· Dosaggio dei nitriti:
NO2- + 7H+ + 6I- = 3I2 + NH3 + 2H2O
Fonte: https://www.docenti.unina.it/downloadPub.do?tipoFile=md&id=130157
Sito web da visitare: https://www.docenti.unina.it
Autore del testo: non indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve