I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Modulazione di portante sinusoidale con segnali analogici
Il significato del termine modulazione nell’ambito delle telecomunicazioni viene usato per indicare la trasposizione dell’informazione presente in un segnale di partenza, detto modulante, in modo che tale informazioni venga associata a un secondo segnale, detto portante, per ottenere un segnale risultante, detto segnale modulato, avente caratteristiche differenti dal segnale di partenza, ma medesimo contenuto informativo.
Le ragioni che giustificano l’uso delle operazioni di modulazione e demoludazione sono molteplici; le più importanti sono le seguenti:
Grazie alla traslazione di banda è possibile ottenere, attraverso la modulazione, l’adattamento del segnale alla banda passante del canale, che ne deve contenere lo spettro (si pensi per esempio alla trasmissione dati su linea telefonica, che richiede dispositivi di modulazione e demoludazione denominati modem). In molti casi inoltre il mezzo trasmissivo presenta attenuazione minima a una specifica frequenza, per cui è desiderabile traslare lo spettro del segnale nelle vicinanze di tale frequenza;
La modulazione consente di trasmettere contemporaneamente attraverso lo stesso supporto fisico (cavo o spazio) segnali che, se trasmessi in banda base,risulterebbero avere spettri sovrapposti, con conseguenti effetti di interferenza reciproca. Mediante la modulazione è possibile allocare la banda occupata da ciascun segnale in un intervallo di frequenze diverso, in modo da poter successivamente separare ciascun segnale da tutti gli altri mediante filtri passa-banda, come avviene per esempio nelle trasmissioni radiofoniche e televisive (multiplazione FDM);
Nel caso di trasmissioni di onde elettromagnetiche si ha la massima emissione di potenza se le dimensioni delle antenne sono dello stesso ordine di grandezza della lunghezza d’onda del segnale da trasmettere. A titolo di esempio, a un segale di frequenza f=5kHz è asociata una lunghezza d’onda landa=c/f=60km; per trasmettere tale segnale efficientemente senza modulazione sarebbe necessaria un’antenna dalle dimensioni proibitive. Se lo spettro del segnale viene traslato a più alte frequenze, si riduce la lunghezza d’onda con conseguente riduzione delle dimensioni ottimali dell’antenna.
Poiché una portante sinusoidale è caratterizzata da tre parametri (ampiezza, frequenza e fase), può essere modulata mediante tre metodi, consistenti nel variare uno di questi tre parametri.
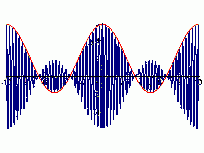
La modulazione di ampiezza, in sigla AM (Amplitude Modulation), consiste nel variare, istante per istante l’ampiezza di una portante sinusoidale in funzione del valore del segnale modulante.
Nella figura sono rappresentati (a) il segnale modulante, (b) il segnale portante e (c) il segnale modulato.
(a)
(b)
(c)
Indicando il segnale portante con 
e il segnale modulante con 
l’onda modulata ha un ampiezza variabile, determinata dal valore costante Vp più un termine pari al segnale modulante 
, preventivamente amplificato o attenuato in modo che abbia un’ampiezza idonea alla modulazione.
L’espressione del segnale modulato è pertanto 
che può essere scritta nella forma 
in cui m è una quantità definita indice o profondità di modulazione.
L’indice di modulazione m è compreso fra zero ed uno; per m>1 l’onda modulata risulta distorta come rappresentato in figura.
L’espressione del segnale modulato 
può essere scritta anche nella seguente forma:
da cui si deduce lo spettro di frequenza dell’onda modulata. Poiché l’espressione è costituita dalla somma di più termini sinusoidali, essa rappresenta lo sviluppo in serie di Fourier del segnale modulato, in cui è possibile individuare tre termini: il primo termine è di frequenza fp (ovvero frequenza della portante); il secondo è di frequenza fp-fm ed è detto riga laterale inferiore; il terzo è di frequenza fp+fm ed è detto riga laterale superiore.
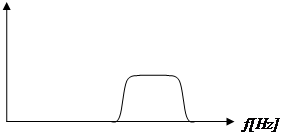
Nel caso di un segnale qualsiasi, avente uno spettro a righe o continuo come quello della figura (a), è possibile pensare la portante modulata da ogni singola componente di Fourier del segnale: ogni componente dà luogo a una riga inferiore e a una superiore per cui lo spettro risultante ha forma riportata in figura (b).
Figura (b)
Figura (a)
f[Hz]
Dallo spettro in figura (b) è possibile determinare la larghezza di banda BAM dal segnale modulato:
BAM = fp+fmax-(fp-fmax) = 2fmax
Se l’occupazione in banda base coincide con fmax, perché la frequenza più bassa è nulla o è trascurabile, l’occupazione di banda del segnale modulato risulta doppia rispetto all’occupazione in banda base.
La demodulazione o rivelazione è un'operazione che consente di estrarre, da un segnale modulato in ampiezza, l'informazione in bassa frequenza. Nell'operazione di demodulazione si realizza una conversione di frequenza che a partire dallo spettro del segnale AM permette di ricostruire il segnale in banda base.
La demodulazione è, normalmente, realizzata utilizzando un dispositivo non lineare, che nella maggior parte dei casi è un diodo, seguito da un filtro passa basso in grado di ricostruire l'inviluppo del segnale AM.
Il rivelatore che trova le maggiore applicazione pratica è il rivelatore d'inviluppo a diodoAl fine di migliorare l’efficienza della modulazione AM in termini di potenza trasferita è possibile non trasmettere la portante. La modulazione che ne deriva è la DSB-SC (Double Side-Band Suppressed Carrier) o più semplicemente DSB,e il relativo spettro è rappresentato in figura.
Spettro del segnale modulante
Spettro del segnale modulato
f
Al fine di ottenere un segnale DSB è sufficiente applicare il segnale modulante e la portante agli ingressi di un moltiplicatore. Consideriamo infatti un segnale modulante sinusoidale
vm(t) = Vm cos(ωmt) e riporto l’espressione del segnale modulato in AM a portante trasmessa
vAM(t) = [Vp+Vm cos(wmt)] cos(wpt) = Vp cos(wpt) + Vm cos(wmt) cos(wpt).
Si può notare come togliendo dall’espressione del segnale modulato in AM a portante trasmessa il termine relativo alla portante si ottiene v(t)= Vm cos(wmt) cos(wpt).
L’inconveniente della DSB consiste nella necessità di ricostruire la portante in ricezione, per permettere la demodulazione, ed è difficile il reinserimento esatto, senza che si abbiano distorsioni. Spesso, in pratica, non si elimina completamente la portante, ma la si trasmette ad un livello ridotto, in modo da facilitare la rigenerazione in ricezione.
I metodi di modulazione esaminati in precedenza danno luogo a un’occupazione in banda doppia rispetto a quella in banda base. Dato che le due bande laterali sono simmetriche rispetto alla frequenza centrale, è possibile eliminare, oltre alla portante, una delle due bande migliorando di un fattore due l’efficienza sia in termini di potenza che di occupazione di banda. Il tipo di modulazione che deriva da questa operazione è denominata SSB (Single Side-Band).
Hm [f]
(a)
(b)
Hm [f]
(c)
H [f]
AV
Un secondo metodo che elimina la necessità di filtri, è detto metodo dello sfasamento. Supponendo di partire da un segnale modulante sinusoidale consideriamo un segnale DSB
e supponendo di voler eliminare la riga laterale inferiore, l’espressone del segnale SSB è 
.
Applicando la formula di addizione cos(α+β)= cosα cosβ – senα senβ tale segnale può essere espresso come
Pertanto il segnale SSB può essere visto come la differenza di due segnali DSB, uno dei quali si ottiene sfasando di π/2 sia la portante che il segnale modulante. Se il segnale modulante ha un andamento qualsiasi, le considerazioni precedenti non cambiano.
L’inconveniente della SSB è lo stesso della DSB: la difficoltà a reinserire la portante, in modo da potere demodulare il segnale trasmesso senza distorsione.
La modulazione di frequenza, in sigla FM (Frequecy Modulation), consiste nel variare, istante per istante, la frequenza di una portante sinusoidale in funzione del valore del segnale modulante.
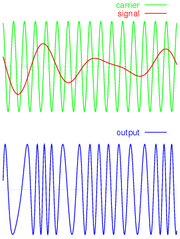
Il valore istantaneo della frequenza f(t) della portante è quindi determinato dal valore a riposo di fp, più un contributo proporzionale al segnale modulante vm(t) (supponendo il segnale modulante sinusoidale):
.
Il parametro ∆f, definto deviazione di frequenza, indica la massima variazione prodotta dalla modulazione sulla frequenza della portante.
Il segnale modulato può essere scritto tramite la seguente espressione: 
avendo indicato con mf la quantità 
definita indice di modulazione.
Come si può notare dalla rappresentazione grafica dello spettro di un segnale FM con modulante sinusoidale è composto da una riga alla frequenza ella portante fp, e da un certo numero di coppie di uguale ampiezza e simmetriche rispetto a fp; tutte le righe inoltre sono distanziate di una quantità pari alla frequenza della modulante.
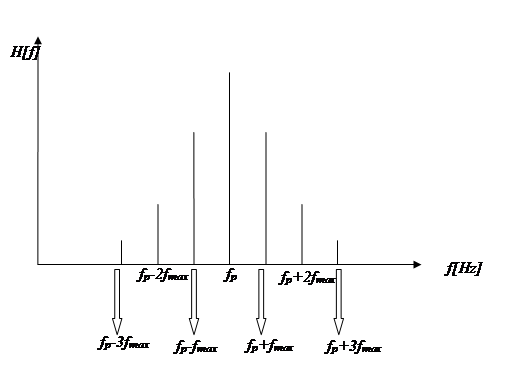
mf
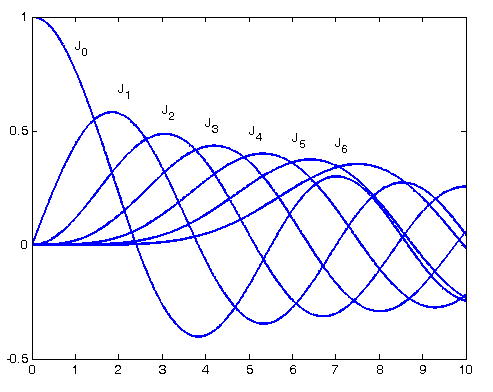
Le ampiezze della portante e delle coppie, nel caso in cui sia Vp=1, sono determinate dai moduli di una famiglia di funzioni J0, J1, J2, ecc., denominate funzioni i Bessel, il cui valore è funzione dell’indice di modulazione mf. Fissato mf, per conoscere il valore delle funzioni di Bessel è possibile dei tabulati o i grafici rappresentati in figura. Se si ha Vp≠1 tutti i valori ricavati devono essere moltiplicati per Vp.
Osservando la figura si può notare che fissato mf, tutte le funzioni di Bessel da un certo indice in poi sono nulle ho hanno valori trascurabili; inoltre il numero delle funzioni non nulle cresce con mf. Risulta quindi che la larghezza di banda FM ha le seguenti caratteristiche:
La determinazione esatta dello spettro FM richiede, per ogni valore di mf, la conoscenza dei valori delle funzioni di Bessel, tuttavia esistono espressioni approssimate che permettono di valutare la larghezza di banda FM, tra le quali la più nota è la formula di Carson
La formula di Carson implica che il numero di copie non nulle è approssimativamente pari a mf+1.
Ricordando che 
la formula di Carson può essere espressa nella forma seguente 
nel caso in cui il segnale modulante abbia un andamento qualsiasi la formula rsta valida, se riferita alla frequenza massima fmax dello spettro del segnale modulante: 
In questo caso ∆f è fissato, e l’indice di modulazione deve essere riferito a fmax: mf= ∆f/ fmax; si osservi tuttavia che ogni componente del segnale modulante modula la portante con un proprio indice di modulazione mf(f)=∆f/f , tanto maggiore quanto più bassa è la frequenza della componente.
Dalla figura delle funzioni di Bessel si può notare che per mf <0,5 sono trascurabili tutte le funzioni da J2 in poi; lo spettro pertanto comprende solo la riga a frequenza della portante e due righe laterali, con occupazione di banda pari a 2fm. per modulazioni con mf>>1 risulta che l’occupazione di banda è determinata principalmente da ∆f, e dipende in piccola misura dall’ampiezza della banda base del segnale modulante.
Fonte: http://www.itiscopernicofe.it/itis/didattic/matdid/5H/Modulazione.doc
Sito web da visitare: http://www.itiscopernicofe.it
Autore del testo: non indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve