I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
DECIBEL E UNITA’ “S”
de IØDBF
DB & DB & Unità “S” (de IØDBF)
GENERALITA’ - Chi si interessa di radioelettronica prima o poi avrà certamente a che fare con i “deciBel”, per certi versi, strani oggetti ben noti in tutti i loro aspetti a quanti sanno ben manipolarli, un po’ meno familiari lo sono invece a quanti ne fanno “prudente” impiego accettandone la presenza con fede ma senza particolare convinzione.Senza stare a riprendere le motivazioni tecnico-fisiologiche che ne determinarono, a suo tempo, l’introduzione, diciamo che non si può parlare di “deciBel” senza parlare di logaritmi. Logaritmi che, fra l’altro, si prestano egregiamente anche in tutti i casi molto frequenti in elettronica in cui si vogliano esprimere numeri piuttosto grandi o particolarmente piccoli.
E’ bene in questa nota introduttiva precisare subito il fatto che una grandezza espressa in deciBel non costituisce mai una misura assoluta bensì è sempre una misura relativa. Assoluta, infatti, può considerarsi la misura di una d.d.p. in corrente continua presente ai capi di un circuito elettrico letta sul voltmetro; questo perché l’elemento di riferimento è il “Volt” che costituisce “invariante” in ogni circostanza.
La stessa cosa non si può dire invece di una misura in “deciBel” nella quale, come si vedrà, il termine di confronto viene scelto di volta in volta in funzione della tipologia d’indagine.
A questo punto prima di continuare a parlare di “deciBel” potrà essere utile un breve richiamo matematico sui logaritmi visto l’importante ruolo che svolgono nei ragionamenti a seguire. Resta ovvio che se l’argomento fosse noto si può saltare direttamente al punto 3.
8 = 
9 = 
= 
10000 = 
Ciò è dire che :
8 si ottiene elevando “la base 2” alla terza potenza e cioè ad “esponente 3”;
9 si ottiene elevando “la base 3” alla seconda potenza e cioè ad “esponente 2”;
100000 si ottiene elevando “la base 10” alla quarta potenza e cioè ad “esponente 4”.
Chiarito questo, il passaggio al “logaritmo” è praticamente immediato. Infatti dagli esempi precedenti deriva direttamente che:
l’esponente 3 del numero 2 è il “logaritmo in base 2” del numero 8;
l’esponente 2 del numero 3 è il “logaritmo in base 3” del numero 9;
l’esponente 4 del numero 10 è il “logaritmo in base 10” del numero 10000.
Pertanto il “logaritmo” di un numero, data una certa “base”, è semplicemente l’esponente a cui bisogna elevare quella “base” per ottenere il numero dato.
Ne discende che, nota la “base” ed il “logaritmo” di un qualsiasi numero, quest’ultimo può essere sempre univocamente determinato (sarà utile nelle trasformazioni inverse per passare, per esempio, da dBw a Watt).
Peculiare proprietà che rende particolarmente interessante l’uso dei logaritmi nelle varie applicazioni consiste nel fatto che al logaritmo di un prodotto può essere sostituita la somma dei logaritmi di ciascun fattore, come pure, al logaritmo di un rapporto può essere sostituita la differenza fra i logaritmi del dividendo e del divisore (il glorioso “regolo calcolatore” che era la “calcolatrice scientifica” degli anni ’60 si basava proprio su questo).
Va da sé come questa proprietà faciliti molto i calcoli in quanto a moltiplicazioni e divisioni è sempre possibile sostituire semplici somme e differenze più immediatamente eseguibili.
Un’ultima nota: nelle considerazioni che verranno esposte di seguito la “base” scelta è “10” ; ciò è dire che qualsiasi numero sarà sempre rappresentato da una potenza di 10 (*).
Corre l’obbligo di rammentare che:
Come fare ad calcolare una potenza ad esponente positivo è cosa nota, basta moltiplicare per se stesso il numero scelto come base tante volte quanto è l’esponente. Ma come si procede se l’esponente è negativo (esponente preceduto dal segno “meno”)?
Beh, è altrettanto semplice: se ne fa prima il reciproco, poi si cambia di segno l’esponente e si eleva a potenza nel modo consueto.
“….e che vor di’ sto reciproco?....” mi par di sentire da parte di qualcuno. Vuol dire semplicemente prendere la potenza, togliere il segno negativo dall’esponente e porla a denominatore di una frazione avente “1” come numeratore.
L’esempio a seguire spiega meglio il tutto.
Sia dato:
questo diventa 
= 
= 
A questo punto con una qualsiasi calcolatrice (**) si calcola quanto fa 1 diviso 1718 e si ottiene 0,00057 che è il risultato di 12 elevato alla -3.
Rinfrescate queste nozioni quale premessa chiarificatrice per gli argomenti a seguire, possiamo finalmente passare ad esplorare il mondo dei “deciBel” .
(*) Da cui la denominazione di logaritmo decimale.
(**) Chi non dispone di una calcolatrice “scientifica” utile per calcolare potenze e logaritmi può vantaggiosamente usare quella inserita in “Windows”. Per fare un po’ di pratica, si provi a scegliere un qualsiasi numero sia positivo che negativo, intero o decimale e se ne determini il logaritmo decimale (generalmente corrispondente al tasto [Log] ). Si elevi quindi il numero 10 a potenza uguale al logaritmo trovato e si vedrà come risultato ricomparire il numero di partenza. Sulle calcolatrici scientifiche l’elevamento al quadrato corrisponde, in genere, al tasto 
mentre l’elevamento a potenza qualsiasi corrisponde al tasto 
. Fare qualche prova per esercizio.
Si vedrà in seguito che mentre, per esempio, ad una potenza di 80 watt corrispondono +19 dBw, al valore doppio di +38 dBw corrisponderà ben altra potenza che non il doppio di 80 W. Infatti a +38 dBw corrisponde la potenza di 6309 W che è ben 79 volte maggiore di 80.
Ed ancor più, quale potenza corrisponde a “0“ dBw ? Probabilmente i meno introdotti nell’argomento potrebbero istintivamente rispondere che a 0 dBw corrisponda una potenza nulla. Sbagliato! Come si vedrà, a 0 dBw corrisponde invece la potenza di 1 Watt, tutt’altra cosa che zero!
A questo punto ce ne dovrebbe essere abbastanza per incuriosire anche i più restii e, pertanto, è giunto il momento di entrare nel tema senza altri indugi.
Si è detto che una misura in deciBel è una misura che scaturisce dal confronto, a mezzo di un rapporto, fra due grandezze omogenee. Volendo confrontare, per esempio, la potenza P1 di un segnale trasmesso con quella P2 dello stesso segnale ricevuto ai capi di una antenna, si effettua per prima cosa il rapporto fra i due valori e successivamente si determina il logaritmo in base 10 di esso.
Il risultato ottenuto, come si vedrà, fornisce una quantità facilmente maneggiabile utile a stabilire un preciso confronto fra le grandezze date.
Per esempio, supponendo che una antenna trasmittente irradi un segnale con la potenza
P1 = 80 W e che ai capi di una antenna ricevente venga misurata una potenza
P2 = 0,000 000 002 W, effettuando un semplice rapporto (non consideriamo al momento il logaritmo) si ottiene:
Fermando il calcolo a questo punto, da quanto ottenuto si deduce che la potenza irradiata è 40 miliardi di volte maggiore di quella ricevuta che, a sua volta, risulta essere 2 miliardesimi di quella trasmessa. Determinazione questa di per sé precisa che, se ci si accontenta, potrebbe esaustivamente fornire il quadro piuttosto esatto della situazione.
Ma si provi ad immaginare una tipica conversazione tecnica fra radioamatori:
“…. Lavoro con una antenna in grado di sviluppare ai morsetti 2 miliardesimi di una potenza trasmessa con intensità 40 miliardi di volte maggiore….. “
Con possibile risposta:
“…. Bene, ma hai provato il megacircuitrone che è capace di fornire 38,5 miliardesimi a fronte di una potenza irradiata solo 26,7 miliardi di volte maggiore?... “ . Certamente potrebbero essere descrizioni esatte ma pochissimo pratiche e, per molti versi, anche un po’ comiche!
E’ qui che l’intervento dei logaritmi serve a riportare tutto a dimensione ragionevolmente più umana e soprattutto pratica.
Infatti il risultato della relazione precedentemente esaminata, calcolandone il logaritmo, diventa:
log
= log
= log 40 000 000 000 = 10,6 (1)
Come si nota, un semplice numero a tre cifre sostituisce quello ad undici cifre determinato in precedenza. A questo punto però sorge il problema di come chiamare detto numero che, per di più, è anche adimensionale risultando dal rapporto di due grandezze omogenee. In altre parole….. 10,6 cosa?? …. Che cosa è questo 10,6 ?
Ebbene, dovendo attribuire un nome a numeri che scaturiscono da ragionamenti di questo genere, si è concordato di adottare il termine “Bel“ in onore dell’illustre inventore d’oltre mare Alexander Graham Bell. Grazie all’introduzione di questa nuova unità di misura, si potrà finalmente affermare molto più praticamente che il trasmettitore in questione irradia una potenza di +10,6 Bel rispetto a quella che appare ai capi dell’antenna ricevente. E’ molto meglio che il numerone di prima, vero?
Essendo però il Bel una quantità piuttosto grande, si è deciso (convenzione internazionale ISO 31 e IEC 27) di adottare il sottomultiplo pari a 1/10 del Bel e cioè il “ deciBel “.
Con questa nuova definizione possiamo finalmente dire…….
“ Signori, il deciBel è servito!”.
Ora è importante notare che proprio perché 1 Bel corrisponde a 10 deciBel, abbreviato 10 dB, (né più e né meno come 10 dm corrispondono ad 1 m), nella espressione generale compare un 10 come fattore moltiplicativo.
Infatti la formula generale riferita a livelli di potenza si presenta così:
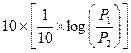[Bel]
da cui segue la nota espressione in decimi di Bel
10 log (
) [dB] (deciBel)
Riprendendo in questa ottica la relazione (1) precedente, si ottiene:
10 x log
=
=
dB
[n.d.r. – il precedente risultato dava +10,6 Bel che concorda perfettamente].
Riprendendo l’esempio precedente, per semplificare ulteriormente il procedimento si sfruttano le proprietà viste per i logaritmi in virtù delle quali al logaritmo del rapporto si può sostituire la differenza dei logaritmi come sotto dettagliato:
10 log (
) =
=
dB
risultato identico a quello precedentemente ma ottenuto con una sottrazione anziché con una divisione …… molto più semplice, vero?
Analogo ragionamento si può fare riferendo il tutto alla potenza trasmessa (P1) anziché a quella ricevuta (P2).
Per fare questo è sufficiente che nella relazione precedente vengano trasposti i valori ponendo P2 al posto di P1 in modo da ottenere:
10 log (
) =
= 10 [(-8,698) – (1,903)] = 10 [-10,6] = - 106 dB
Si nota immediatamente che il numero risultante in valore assoluto è sempre 106, solo che ora è preceduto dal segno meno. Cosa vorrà dire? Vorrà semplicemente dire che il segnale trasmesso con una potenza di 80 W viene ricevuto con una attenuazione di 106 dB.
A questo punto, assunto che sia stata compresa l’essenza di una misura in dB, si rammenta, laddove ce ne fosse ancora bisogno, che dette misure devono in un certo senso essere “adattate” a seconda di cosa si vuole ottenere dalla misura.
Bene, negli esempi precedenti sono stati messi a confronto valori di potenza, sarà la stessa cosa se da confrontare siano invece livelli di tensione? Beh, il procedimento logico è assolutamente identico, varia invece il fattore moltiplicativo che da 10 diventa 20. In forza di ciò, quando si vogliono confrontare due valori di tensione V1 e V2, la relazione diventerà:
20 [ log (V1) – log (V2)] (4.1)
Potremmo, per esempio, avere un quadripolo che ad un livello di segnale in ingresso
Vi= 0,35 Volt restituisce in uscita lo stesso segnale ad un livello Vu = 9,44 Volt.
Senza stare a pensarci su, si tratta certamente di un amplificatore essendo Vu > Vi; ebbene se ne vuole determinare la cosiddetta “funzione di trasferimento”, cioè il guadagno di tensione G e lo si vuole esprimere in decibel.
Sarà allora:
G = 20 [log(Vu) – log(Vi)] = 20 [log(9,44) – log(0,35)] =
= 20 [0,974 – (- 0,455)] = 20 [0,954 + 0,455] = 20 [1,430] = + 28,618 dB
che rappresenta il guadagno in dB dell’amplificatore. Da notare che in questo caso il logaritmo del sottraendo (in grassetto) è negativo perché 0,35 è minore di 1 ed il logaritmo di qualsiasi numero minore di uno è sempre negativo.
Più semplice di così….
Quanti poi volessero sapere da dove diamine salta fuori il fattore moltiplicativo “20” possono proseguire con il prossimo capoverso; coloro che invece riescono ad avere ugualmente sonni tranquilli indipendentemente da ciò, possono passare direttamente al paragrafo 5.
Ebbene, per i più curiosi, riprendiamo la formula relativa al confronto di potenze trattata al para 3:
10 log
è però anche vero che
P = V x I (4.2) ma essendo
I = 
(4.3) sostituendo il valore di I così calcolato nella (4.2) si ottiene
P = V 
da cui compattando sotto forma di potenza si ha
P = 
. (4.4)
Quanto trovato consente di scrivere:
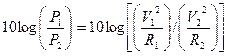
che può essere riscritta
dove R1 ed R2 rappresentano la resistenza (o impedenza) rispettivamente di ingresso e di uscita. Nella casistica generale queste resistenze o impedenze di riferimento sono uguali e cioè R1 = R2 = R (e se non lo fossero si fa in modo che lo diventino con adatte configurazioni circuitali) e pertanto è possibile elidere nell’ultima relazione R1 ed R2 che, essendo uguali, si semplificano ottenendo:
=
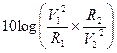Da questa espressione, per la definizione di logaritmo e proprietà ad esso associate, l’esponente “2” del rapporto (V1 / V2) può trasformarsi in fattore moltiplicativo in modo che sia:
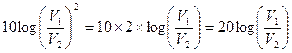
ed anche in questo caso….. “ Signori, il “20” è servito ! “.
5.1 dB e dBw
Cominciamo con i “semplici” dB. Orbene quando ci si trova a dover confrontare, nel senso specificato nei precedenti paragrafi, due generici numeri che esprimono due grandezze elettriche omogenee espresse nella stessa unità di misura, si avrà a che fare con i “dB” senza alcuna ulteriore specificazione.
Negli esempi dati al para 3 e 4 vengono messi a confronto generici numeri relativi a valori di potenza P1 e P2 in Watt come anche valori di tensione V1 e V2 in Volt, in questi casi ed in tutti gli altri analoghi il risultato numerico è caratterizzato da essere sempre espresso in dB. Nella stima in dB del rapporto fra due grandezze, spesso però si preferisce porre il valore unitario come termine di confronto. Infatti, un particolare termine di confronto che si incontra nel quantizzare livelli di potenza è, per esempio, il Watt e, più precisamente,
1 Watt. Ebbene in questo caso si parlerà di di “dBw” che si legge “dBwatt” o “dB su watt”.
Nell’esempio introduttivo al para 3 si è presa in considerazione una potenza di 80 W e si è detto che essa equivale a +19 dBw. Per dimostrare ciò si applica il procedimento che segue che si utilizza ogniqualvolta si vogliano esprimere in decibel valori di potenza rapportati ad 1 Watt.
Applicando la relazione:
vista al para 3, per P1=80 W e P2=1 W, si ottiene:
+19 dBw
Un caso particolare in tal genere di confronto da tener presente è quello in cui la potenza che si vuole “decibelizzare” vale anche essa P1=1 Watt. La relazione appena vista diventa:
dBw
Questo spiega perchè (vedasi para2) 1 Watt di potenza corrisponde a 0 dBw.
Dal punto di vista matematico il procedimento che porta invece da 0 dBw ad 1 W e che vale anche come regola generale è il seguente:
= 1 W (*).
(*) si ricorda che qualsiasi numero elevato a potenza 0 (zero) vale 1.
Da quanto detto dovrebbe essere ovvio che ogni volta si confrontano due valori identici, indipendentemente se Watt, Volt, ecc. , come risultato si otterrà sempre 0 dB. Altrettanto chiaro dovrebbe essere che 0 dB risulta povero di significato se non sono note le grandezze a cui detto termine è riferito.
5.2 dBw e dBm
Talvolta è opportuno, quando le potenze in gioco sono sufficientemente piccole, considerare come livello di confronto 1 mW. Applicando sempre la stessa relazione nell’ipotesi si voglia sapere a quanti dBm (decibel su milliwatt) corrispondono 0,76 W, si ottiene:
+28,8 dBm. (es. 5_1)
>> ricordo che 0,76 Watt corrispondono a 760 mWatt
I più attenti dovrebbero già aver intuito il vantaggio che ne deriva dall’utilizzare il valore unitario come termine di confronto…. Riflettendoci su, balza evidente come in tal caso il valore del logaritmo del termine di confronto è sempre nullo, dato che trattasi del logaritmo dell’unità che vale sempre zero. Pertanto per determinare il valore in dB è sufficiente calcolare il logaritmo della sola grandezza d’interesse e moltiplicarlo per il conveniente fattore moltiplicativo che sarà 10 o 20 a seconda che si stia trattando potenza o tensione.
In quanto poi a dBw, dBv ecc., si dovrebbe ormai aver abbondantemente compreso “il trucco”, in quanto per:
- dBw termine di confronto è 1Watt,
- dBv termine di confronto è 1 Volt,
- dBm termine di confronto è 1 mWatt (
Watt),
- dBµV termine di confronto è 1 µVolt (
Volt) …. e così via.
Ovviamente c’è sempre da ricordare che, qualunque sia il caso, le grandezze coinvolte, oltre che omogenee, devono essere espresse nella stessa unità di misura. Con questo si vuole intendere che nel caso dei dBm tutto deve preventivamente essere espresso in milliwatt, ed, analogamente, nel caso dei dBmV o dBµV tutto deve essere espresso rispettivamente in millivolt o microvolt e così via. Nell’esempio precedente (es. 5_1) infatti, prima di procedere al calcolo, la potenza in gioco è stata convertita da 0,76 Watt a 760 milliWatt per poter essere congrua col termine di confronto di 1 mW.
5.3 dBi e dBd - Procedendo, parlando questa volta di antenne, si incontrano i dBi…. la cosa è un po’ più complicata, ma niente panico..! E’ pur sempre lo stesso “refrain”….. qualcuno ha pensato bene di esprimere il guadagno che una antenna presenta verso una certa direzione, confrontandolo con quello offerto da una antenna campione isotropica (che irradia in ugual maniera in tutte le direzioni) scelta come riferimento (ecco il perché della “i” come pedice aggiunto a suffisso di dB per leggere dBi). Questo genere di misura non è proprio alla portata di tutti in quanto, oltre che per difficoltà di calcolo, difficilmente si dispone di una antenna isotropica campione, degli strumenti necessari nonché dell’ambiente “anecoico”, cioè perfettamente isolato elettromagneticamente dall’esterno e privo di riflessioni, necessari per effettuare detta misura. Niente vieta però che detto confronto possa utilmente essere effettuato fra l’antenna in studio ed una, assunta come campione, di cui però sia noto il guadagno con buona precisione. Comunque, l’applicazione nella pratica sperimentale delle conoscenze sviluppate in questo campo ha permesso di determinare che un dipolo semplice a ½ λ presenta un guadagno di circa +2,15 dBi nei confronti di una antenna isotropica. Partendo da questo dato ed utilizzando ulteriori algoritmi la cui trattazione esula da queste note, sono stati compilati programmi di calcolo applicabili al progetto di antenne (tipicamente Yagi) implementati su pc che forniscono, in base al guadagno desiderato, elementi di progetto per la realizzazione di eccellenti autocostruzioni. Con l’ausilio di tali programmi, dimensionando opportunamente radiatore ed elementi passivi, si riescono a realizzare direttive che possono arrivare a presentare fino a 13
14 dBi di guadagno (vds. programma freeware YO; progetto e costruzione di antenne VHF di I0HJN e IK0BDO).
Ad ogni buon fine, può essere utile tenere a mente le seguenti relazioni di trasformazione:
dBd = dBi - 2,15
dBi = dBd+ 2,15
dove “dBd”, differentemente da dBi, rappresenta il guadagno di una antenna reale riferita ad un dipolo di riferimento altrettanto reale ma impiegato come campione di cui sono noti parametri di funzionamento e guadagno (può essere, come già accennato, una direttiva centrata sulla stessa frequenza di cui sia precisamente noto il guadagno).
Su questi dati occorre porre molta attenzione quando si esaminano i “data sheet” di antenne commerciali! Una non rara abitudine da parte di varie aziende costruttrici è infatti quella di esprimere il guadagno presentato da una antenna in generici dB che, in mancanza di elementi di confronto o ulteriori specificazioni, è assolutamente privo di significato. E’ evidente invece come il guadagno espresso in dBd riesca a caratterizzare un’antenna molto meglio e senza equivoci. Infatti in dBd, come già detto, viene espresso il guadagno che, per esempio, una antenna Yagi presenta rispetto ad un’altra, scelta come campione. Quindi dovrebbe anche essere acquisito che detto valore in dBd, sommato all’incremento isotropico di + 2,15 dBi, fornisce infine il vero guadagno in dBi dell’antenna in questione.
Ad ulteriore chiarimento, note le relazioni su esposte, dovendo scegliere per esempio fra due antenne A e B di cui una presenta un guadagno G1=10 dBi ed un’altra un guadagno G2=9 dBd, sarà da scegliere la seconda perché, a conti fatti, presenta un maggior guadagno in dBi (isotropico) essendo
G2(dBi)= 9dBd+2,15dBi = (9+2,15)dBi = 11,15 dBi (*)
Infatti, come si è detto, il guadagno isotropico G2 presentato dall’antenna B vale il guadagno proprio in dBd sommato a 2,15 dBi che costituisce l’incremento di guadagno rispetto ad una antenna isotropica teorica.
(*) Attenzione: dBd e dBi sono sempre unità di misura omogenee (quindi sommabili) che esprimono esattamente identico genere di grandezza anche se pertinenti a diversa tipologia d’antenna. Dire che una Yagi
ha un guadagno di 9dBd è lo stesso che dire che la stessa ha un guadagno di 11,15 dBi.
6. UNITA’ “S” - Prima di concludere questa escursione nel mondo dei dB, si ritiene opportuno prendere in considerazione l’unità “S” impiegata negli “S-Meter” . Questa unità che tutti usano ma che non tutti sanno cosa esattamente rappresenti, come noto, è stata introdotta per dare una misura facilmente fruibile caratterizzante l’intensità dei segnali ricevuti dai radioricevitori. Se ne chiarirà, pertanto, la sua origine e si esporranno le relazioni che la caratterizzano. In un breve scritto su questo argomento, Angelo Brunero dell’A.I.R. (Associazione Italiana Radioascolto) rammenta che le unità “S” lette sull’ “S-Meter” di un ricevitore sono unità assolutamente “arbitrarie” con la caratteristica di essere strettamente correlate con i dB, data la notevole escursione della potenza con cui i segnali radio possono essere ricevuti (dinamica fino a 108 // 110 dB per i ricevitori altamente professionali, come dire segnali che possono variare in potenza con un rapporto da 1 fino a 66 000 000 000 di volte ! (*) ).
(*) Si provi, per esercizio, a verificare quanto affermato. Con le nozioni di cui alle pagine precedenti si dovrebbe essere in grado di farlo. E’ sufficiente, infatti, trasformare in dB il rapporto appena dato ricordando che, trattandosi di potenza, il fattore moltiplicativo è 10.
Per iniziare precisiamo che per questo genere di segnali, a seguito di convenzione internazionale, è stata a suo tempo stabilita una scala di unità “S” da “1” a “9” ad intervalli unitari seguita, dopo il “9”, da ulteriori tre intervalli di 20 dB equamente spaziati; si tratta, in definitiva, della nota scala:
S 1 2 3 4 5 6 7 8 9 +20 +40 +60dB
Arbitrariamente, infatti, con accordo internazionale si è convenuto far corrispondere l’unità “S 9” al segnale di 100µVolt d’ampiezza visto su una impedenza di 50 Ω (tipicamente impedenza d’ingresso antenna di un RTX) sviluppante su questa una potenza di 0,2 nWatt. Contestualmente, a salire in sequenza a partire da S1, è stato stabilito che ad ogni intervallo unitario dovesse corrispondere il raddoppio del segnale. In altre parole ad “S2”corrisponde un segnale d’ampiezza doppia rispetto a quello corrispondente ad “S1”, ad “S3” un segnale di ampiezza doppia rispetto ad “S2” e così via fino ad “S9”. Per ricavare analiticamente quanti dB sono sottesi in ciascuno di tali intervalli si può partire, per esempio, da un segnale V1=0,1µVolt (tipico di un ricevitore estremamente sensibile), e si applica la nota relazione [4.1§4] sull’intervallo compreso fra detto valore e quello di valore doppio V2=0,2µV. Il procedimento algebrico da seguire, già visto in precedenti applicazioni, è di seguito illustrato.
.
Sono noti i valori V1=0,1µV e V2=0,2 µV che sostituiti nella relazione [4.1 §4] danno:
dB = 20×(logV2 – logV1) = 20×(log 0,2 – log 0,1) = 20×[-0,698 – (-1)] =
= 20×(-0,698+1) = 20×( -0,301) = + 6,02 ≈ + 6 dB
che sono esattamente i dB aspettati in questo caso e che risultano ogniqualvolta si ha un raddoppio di tensione quali che ne siano i valori coinvolti.
E’ facile provare a questo punto che ogni intervallo intercorrente fra “S1” ed “S 9” comprende 6 dB, il che serve a confermare che ogni raddoppio dell’ampiezza del segnale comporta 6 dB di incremento e viceversa (attenzione: si sta parlando di tensione non di potenza! Pertanto nei calcoli il fattore moltiplicativo è 20).
A partire invece da “S 9” (segnali forti e fortissimi) ad ogni ulteriore intervallo sull’ “S-meter” corrisponde un incremento d’ ampiezza di 10 volte a cui, a sua volta, corrisponde l’incremento di 20 dB. Si può verificare ciò applicando la medesima relazione su uno qualunque di questi intervalli.
A titolo di esempio, si possono prendere i valori 100 µV ed 1 mV (1mV= 10volte100 µV) corrispondenti rispettivamente a “S9” ed “S9+20”, procedendo come sopra indicato si otterrà come risultato esattamente 20dB e cioè il “+20” riportato sull’S-Meter (allo scopo si può anche utilizzare il programmino excell compreso nel foglio “dB_tensioni_ver4” che converte in dB il rapporto fra due tensioni) Come noto, dopo il “+20”, la suddivisione della scala prosegue poi con +40 e +60.
Riepilogando, a costo di ripetersi, le unità di scala da S1 ad S9 sono unità arbitrarie a cui corrispondono però precisi livelli di segnale generalmente espressi in µVolt; le letture +20 // +40 // +60 danno invece il valore numerico di quanti dB il livello del segnale supera 100µV (cfr. tabella “Unità“S”<>tensione” in appendice ed anche in excell “dB_tensioni_ver4”).
Per la tranquillità dei più intolleranti alle formule, va detto che la tabella delle corrispondenze “Unità S // Tensione può essere realizzata anche senza nessun calcolo.
Infatti basta sapere che ad S1, sulla la maggior parte degli S-Meter, corrisponde un segnale di 0,4 µV (con più precisione 0,3962 µV) perché, raddoppiandolo in corrispondenza delle unità successive fino ad S9 e decuplicandolo per ogni intervallo compreso fra S9 e +60, sia possibile costruire l’intera tabella delle corrispondenze….
Però, vogliamo veramente fare come il calabrone, pesante insettone che, aerodinamicamente parlando, non potrebbe volare…. eppure vola…. ma non sa perché....
..Anyway… tornando ai nostri argomenti, si potrebbe considerare sufficiente quanto esposto, ma…. la schiera degli “irrecuperabili”, che pur esiste, potrebbe avere ancora l’insana curiosità di voler conoscere quale è la potenza in Watt (ovviamente frazioni molto piccole di Watt) che corrisponde al segnale letto sull’ “S-Meter”. Ebbene, costoro dopo aver preventivamente effettuata la lettura sull’S_Meter, ne determineranno prima il corrispondente valore in Volt (espresso in frazioni di Volt e desumibile dalla tabella unitàS//Volt più volte menzionata) ed applicheranno poi la relazione (4.4 §4), tenendo conto del valore dell’impedenza d’ingresso (supposta sempre di 50 Ω).
[n.d.r. possono anche, con minor soddisfazione ma più rapidamente, ottenere il risultato cercato leggendolo direttamente nella tabella precalcolata “Unità”S”//Potenze” in appendice oppure, entrando nell’apposito riquadro del foglio excell col dato in Volt estratto dalla tabella “Unità “S”//Tensioni” in appendice (foglio excell “dB_potenze_ver3” riquadro “passaggio Volt//Watt)].
A titolo di esempio, si vuole sapere quale potenza elettrica sviluppa su 50 Ω un segnale di S7. Con il calcolo visto in precedenza o dalla tab.”Unità S<>Tensioni” posta in appendice, prima si determina che al segnale di S7 corrispondono 25µV, successivamente, tenendo presente che questi 25µV sono applicati su una impedenza di 50 Ω, si applica la relazione (4.4 §4):
P=
=
=
= 12,5×
Watt oppure 12,5 pWatt.
Anche in questo caso, come accennato in precedente n.d.r., è stato previsto un programmino “passaggio da Volt a Watt” nel foglio excell “dB_potenze_ver3” per eseguire automaticamente questo calcolo (è sufficiente inserire il valore della tensione nel apposito riquadro per ottenere il risultato cercato).
Infine una utile indicazione per la taratura degli “S-Meter”. Laddove questa operazione si possa effettuare e disponendo di un generatore idoneo, occorre porre in ingresso antenna del ricevitore un segnale calibrato di ampiezza pari a 100 µV adattato per l’impedenza di 50 Ω (generalmente tutti i generatori di segnale sono predisposti per questa impedenza di uscita; ovviamente bisogna usare per il collegamento un cavetto di impedenza pari a 50 Ω), quindi occorre agire sull’apposito controllo nel ricevitore in modo da portare l’indice dell’ “S-Meter” su S9.
A seguito di detta regolazione, anche i restanti punti della scala dell’ “S-Meter” dovrebbero coincidere con le corrispondenze previste dalla solita tabella “UnitàS//Tensione” senza altri interventi. Per eccesso di zelo, si potrebbe comunque verificare la corrispondenza aspettata negli altri punti della scala “S” ponendo in ingresso antenna gli appropriati livelli di segnale, e leggerne la corrispondenza sull’”S-Meter”.
7. A questo punto si è certamente compreso come l’applicabilità dei “decibel” possa essere limitata solo dalla fantasia e dal risvolto pratico dell’impiego; un portatore sano di “decibelite” sarebbe portato a trasformare in decibel tutto quanto gli capita sotto mano. Noi per il momento ci fermiamo qui con la ragionevole certezza di aver fornito almeno uno strumento di base su cui poter sviluppare ulteriori applicazioni.
Come appendice, sono sinteticamente riportate formule e tabelle che maggiormente si incontrano nella pratica e che possono costituire interesse per i radioamatori, inoltre alcuni fogli excell sono resi disponibili per le applicazioni esposte e che possono essere anche utilizzati in modalità incrociata a seconda dei casi in studio.
Appendice >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Guadagno riferito a potenze:
G =10 log (
) =
Guadagno riferito a tensione:
G =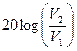 
= 20 [log(V2) – log(V1)]
Passaggio da dB a Watt oppure da dB a Volt
(applicabile solo quando la potenza di riferimento è unitaria)
il valore in dB , come indicato il valore in dB, come indicato
a =
a = 
2) La potenza in Watt vale 2) La tensione in Volt vale
P = 
Watt V = 
Rapporto onde stazionarie SWR, coefficiente di riflessione “ρ “, perdite di ritorno (return loss) “ar”
ρ = 
SWR variabile fra 1 ed infinito;
SWR=
ρ variabile fra 1 (caso di riflessione totale)
e 0 (nessuna riflessione )
perdite di ritorno “ ar ” (return loss)
Questo parametro esprime in decibel l’entità della riflessione in rapporto alla situazione di riflessione totale nel cui caso ρ =1. ed ar = 0 dB.
ar = 20 [log(ρ)-log(1)] in dB
per esempio con SWR=1,002 il coeff di riflessione è ρ = 0,001 e cioè l’uno per mille a cui corrisponde un return loss che si attesta a 60 dB sotto 0 dB.
Applicando le formule date si ricava la tabella a seguire
SWR ρ ar [dB]
dBi = dBd + 2,15
dBd = dBi - 2,15
------------------------------------------------------------------------------------------------------------------
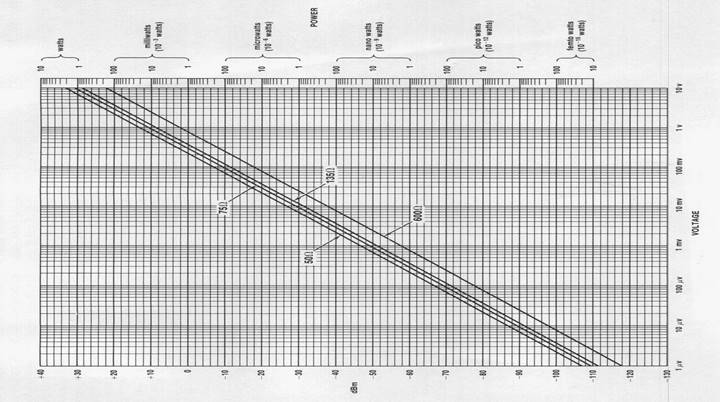
Diagramma di conversione diretta ed inversa da dBm a Watt e frazioni di Watt.
Da dBm a Volt, mVolt e µVolt in funzione dell’impedenza (utilizzare le rette oblique).
Corrispondenze: Unità “S” <> Tensione Unità “S” <> Potenza |
|
|
|||||||
|
|
||||||||
S-Meter // Tensione
Per unità da S1 a S9 i valori di tensione raddoppiano ad ogni intervallo.
Ogni intervallo compreso fra S1 ed S9 è ampio 6 dB.
Per unità da S9 a S9+20 // da S9+20 a S9+40 // da S9+40 a S9+60 i valori
di tensione si decuplicano ad ogni intervallo (ampiezza intervalli 20 dB).
S-Meter //Potenza
La tabella “Unità “S”// Potenza” si costruisce applicando la formula [4.4 §4] (*):
Il valore della tensione “V ” relativa al segnale corrispondente alle unità “S” va estratto
dalla tabella “S_Meter//Tensione”
(*) Vedasi anche foglio excell “db_potenze_ver3” riquadro “passaggio Volt//Watt su 50Ω”-
oooooOO0OOooooo
Tabelle Excel
Tutte le formule sono state quindi applicate in fogli di lavoro Excel, qui appresso riportati, che possono essere immediatamente avviati ed utilizzati mediante un doppio click nelle relative schermate .
Comparirà l’effettiva finestra di lavoro di Excel nella quale sarà possibile cliccare col tasto sinistro del mouse i valori da cambiare: dando “Enter” il risultato relativo al calcolo verrà aggiornato.
Se, durante le prove che si effettuano si notasse che il valore richiesto non varia, basterà cliccare sopra il risultato, sempre col tasto sinistro, per ottenere il dato aggiornato.
Si ricorda, inoltre, che le cifre decimali è obbligatorio separarle con la virgola [“,”].
Data la complessità della pagina occorrerà, per rendere la lettura più agevole, ingrandirla tramite lo zoom, prima del doppio click, almeno al 200 %.
>>> IØDBF se ipse cum magna tribolazione fecit mensis Octobris AD MMIX ad usum Radio-Amatoriorum <<<
Fonte: http://www.calvibit.net/files/DECIBEL%20%20E%20%20UNITA%20S.doc
Sito web da visitare: http://www.calvibit.net/
Autore del testo: non indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve