Fisica energia teoria e formule

ENERGIA – teoria e formule
In altri appunti abbiamo introdotto l’Energia, evidenziandone gli aspetti essenziali e descrivendo i tre modi in cui si manifesta –cinetica , potenziale , Lavoro-. Però, per poter utilizzare utilmente l’energia nelle applicazioni, è necessario saper calcolare l’energia. E’ evidente infatti che per eseguire una qualsiasi attività è necessario produrre/consumare energia: ma se tutto ciò che sono in grado di dire fosse “questo lavoro mi consuma più energia di quest’altro… qui spendo tanta energia, là un po’ di meno… qui produco un po’ di più che di là…” e simili, io non sarei mai in grado di progettare la mia attività.

Come misurare l’energia è un problema che è stato dibattuto fin dal 1.600. L’analisi corretta è stata portata a termine nel 1686 da un grande scienziato e filosofo del passato, Gottfried Leibniz.
Energia potenziale di un corpo sollevato (Energia potenziale della forza-peso)
Leibnitz ebbe l’intuizione di misurare l’energia attraverso l’energia muscolare: in altre parole, tentò di misurare l’energia tenendo conto dello sforzo che un muscolo deve eseguire nel sollevare un peso. Leibnitz arrivò a questa fondamentale proprietà:  “l’Energia per sollevare una massa m di un tratto h è proporzionale al prodotto m×g×h” .  Adesso vedremo come Leibnitz è giunto a questa conclusione.

Supponiamo di voler sollevare una massa m con una carrucola (vedi figura 1). In questo caso io spendo energia ma di tipo muscolare, come posso osservare tenendo conto che nel girare la carrucola io mi stanco: chiamo EM questa energia.

Adesso vediamo da cosa dipende EM. Supponiamo di avere girato la carrucola 5 volte e di avere speso un’energia muscolare EM. Se vogliamo sollevare un secondo peso uguale al primo del medesimo tratto h dobbiamo girare la carrucola per altre 5 volte spendendo una seconda volta la stessa energia EM e così via. In altre parole se fissiamo l’altezza di sollevamento, il numero di giri e conseguentemente l’energia muscolare spesa è direttamente proporzionale alla massa totale sollevata (nel nostro caso, spendiamo un’energia EM per ogni massa m sollevata di un tratto h). Posso scrivere:
EM   a   m                             (1)
Supponiamo adesso di voler sollevare la stessa massa m per un tratto doppio: dovrò girare la manovella per 5x2 volte = 10 volte e spenderò così 2·EM. Dunque, l’energia spesa è direttamente proporzionale all’altezza di sollevamento h. Posso scrivere allora:
EM   a   h                              (2)                             
Infine; supponiamo di andare sulla Luna, dove g è minore: nel sollevare la stessa massa dello stesso tratto h io spenderò una minor energia che sulla Terra, perché la forza-peso sulla Luna è minore. All’opposto, se andassi su di un corpo celeste dove g è il doppio di quello sulla Terra, la solita massa m peserà il doppio ed io dovrei fare il doppio della fatica, cioè spenderei 2×EM. Perciò, al raddoppiare di g raddoppia anche EM e dunque:
EM  a  g                                 (3)
In conclusione, unendo le proporzionalità (1) , (2) , (3) ottengo:
EM   a  m·h×g                       (4a)
Scrivendo la proporzionalità (4a) come uguaglianza scrivo:
EM = c×m×g×h                       (4b)
Il valore della costante c è arbitrario e dipende dalla scelta delle unità di misura. Universalmente, si pone c=1, cosicché possiamo scrivere:
EM = m×g×h                          (4c)
Poiché l’energia muscolare EM è stata spesa per innalzare la massa m del tratto h è evidente che la massa m ha immagazzinato l’energia EM; dunque siamo di fronte ad un’energia potenziale (U) e perciò posso dichiarare che m×g×h è la formula dell’energia potenziale di un corpo sollevato.
Potenziale del peso:  U = m×g×h             (5)

Energia cinetica
Se lascio cadere la massa m dall’altezza h essa arriva al suolo con una certa velocità finale VF. E’ chiaro che quando è giunta al suolo tutta la sua energia potenziale è stata spesa, trasformandosi nella velocità VF o meglio in energia cinetica dovuta alla velocità VF. Troviamo adesso la formula che ci permette di calcolare tale energia cinetica.

Poiché alla fine della caduta tutta l’energia potenziale si è trasformata in energia cinetica (K) scrivo: K = m×g×h. Ora devo trasformare questa equazione in modo da far apparire la velocità V, che è la grandezza da cui dipende K. Si possono fare queste considerazioni:
durante la caduta la massa m è sottoposta all’accelerazione terrestre, cioè aCADUTA = g. Il tratto di caduta h lo spostamento che avviene con moto accelerato e perciò vale la formula:
DP = h = ½×a×Dt2 + Vi×Dt    , con Dt il tempo di caduta. Nel nostro caso Vi=0 (la massa parte da ferma) --->    
          h = ½×g×Dt2                                                             (6)

Ora punto devo tirar fuori V. So che dopo un tempo di caduta Dt la velocità è passata da “0” a ad un valore V secondo la formula: V = a×Dt ---> V = g×Dt ; ricavando Dt ottengo: Dt=V/g ; sostituendo nella (6) ho:
h = ½×g×V2/g2 = ½×V2/g.
Sapendo che K = m×g×h , sostituisco h:   K  = m×g×½×V2/g  ---> 
--->    K = ½×m×V2                                           (7)
L’eq. (7) è la formula che mi permette di calcolare l’energia cinetica di un corpo in movimento.
Lavoro
Adesso dobbiamo trovare l’equazione del Lavoro. Poiché esso è la grandezza che trasferisce energia da una forma all’altra o da un corpo all’altro, è chiaro che esso dipende dalla forza agente: più grande è la forza, maggiore è la spinta e più energia trasferisco.
Inoltre, per poter spingere è necessario che il punto di applicazione della forza sia spostato: in altre parole, non posso spingere un oggetto tenendo il braccio immobile, per quanto forte io sia. Dunque, il Lavoro dipende pure dallo spostamento del punto di applicazione della forza.
Per trovare l’eq. del Lavoro, facciamo una semplice considerazione: supponiamo che una forza F0 spinga una massa m all’inizio immobile per un tratto DP parallelo a se stessa (nota che in questo esempio F0 è parallelo allo spostamento DP e perciò consideriamo il caso in cui F0 e DP sono paralleli), portando la sua velocità da 0 a VF.
E’ chiaro che alla fine la massa m ha acquistato un’energia cinetica K = ½×m×V2, come mostra l’eq. (7): questa energia è stata chiaramente trasferita dalla forza F0 e perciò rappresenta il suo Lavoro: Lavoro = energia cinetica trasferita = ½×m×V2 . Bisogna trasformare quest’equazione in modo da mettere in evidenza il ruolo della forza F0 e dello spostamento DP. Come prima, usiamo le formule del moto accelerato:
V = aDt + Vi = (Vi=0) = aDt   --->   L=½×m×(a×Dt)2 = ½×m×a2×Dt2  ---> (separando i fattori in due termini opportuni)   --->   L = (½×a×Dt2)×(m×a) ;  adesso teniamo conto che in un moto accelerato si ha DP= ½×a×Dt2 e che il II Principio della Dinamica afferma che F=m×a , perciò possiamo scrivere:
L = DP×F0                                     (8)      -caso di una forza parallela allo spostamento-

LAVORO E FORZA OBLIQUA
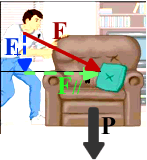Abbiamo detto all’inizio del corso che la forza non è un numero ma un vettore, cioè possiede anche una direzione ed un verso. Come influisce la direzione della forza sul Lavoro? Per comprenderlo, consideriamo il caso in cui F0 e DP non sono paralleli ma formano invece un angolo J.

 Quando spingiamo su un oggetto appoggiato sul pavimento, per esempio una poltrona come in figura 2, l’unica responsabile dello scivolamento orizzontale della poltrona è la componente orizzontale della forza (F//): la componente perpendicolare (F^) o la forza peso della poltrona  (P) non danno alcuna spinta orizzontale e perciò non modificano l’energia cinetica della poltrona. Per cui se lo spostamento avviene in direzione perpendicolare alla forza, essa non compie lavoro.

 Vediamo lo stesso concetto con un secondo esempio. Consideriamo prima di tutto un corpo di massa m lasciato cadere liberamente in aria (vedi figura 3). Su tale corpo agisce la forza-peso P diretta verticalmente dall'alto verso il basso. Pertanto anche il corpo cadrà lungo la verticale dall'alto verso il basso. Lo spostamento indotto dalla forza-peso e la forza-peso hanno in questo caso la stessa direzione e lo stesso verso ed il Lavoro si calcola come L=m×g×h , come già visto.

Nel secondo caso abbiamo un corpo posto su un piano inclinato. La forza-peso agisce ancora lungo la verticale ma, mentre la sua componente perpendicolare al piano si limita a premere sul tavolo, la sua componente parallela al piano (P//) rimane attiva e spinge il corpo m secondo un moto accelerato lungo il piano inclinato, cambiandone la velocità.
Questi esempi illustrano il fatto che il Lavoro di una generica forza F0  durante uno spostamento DP  è dovuto solo alla componente di F parallela a DP (F//). La formula generale del Lavoro diventa:
L = DP×F//                                            (9)   -   formula generale del Lavoro
      (formula fisica)

Altre formule del Lavoro
Vedremo subito che è possibile esprimere il Lavoro con altre due formule. Sappiamo che F// = F0×cos(J) , e perciò possiamo pure scrivere:  L = DP×F0×cos(J)     (10)   -  formula generale del Lavoro
(formula matematica)

Infine, possiamo spostare cosJ da F0 a DP, scrivendo:  L = DP×cos(J)×F0.

 

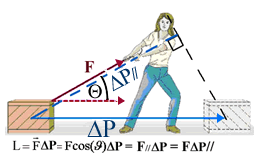
                                      Guarda adesso la figura 4: è evidente che DP×cos(J) è la componente dello spostamento parallela a F0 (DP//): scrivo perciò:

     L = DP//×F    (11)   -   formula generale del  Lavoro
                     (formula geometrica)

 
Segno del lavoro
Se conoscete le proprietà della funzione cos(J) sapete già che cos(J) > 0 per 0≤J≤90° mentre cos(J) <0 per 90°≤J≤180° ---> il Lavoro è positivo nel primo caso, negativo nel secondo (vedi figura 5).

Dal punto di vista geometrico, ciò significa che il Lavoro è positivo quando F// è concorde allo spostamento (F punta dalla parte di DP) mentre è negativo quando F// è discorde (F punta dalla parte opposta a DP). Questo è coerente con ciò che già sappiamo: quando F// è concorde allo spostamento (Lavoro positivo) la forza spinge in avanti il corpo, fornendogli velocità e dunque energia cinetica; all’opposto, quando F// è discorde con DP (Lavoro negativo) essa spinge indietro il corpo, rallentandolo.

Figura 5
LAVORO , POTENZIALE ED ENERGIA CINETICA
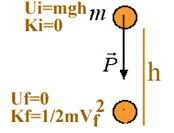Adesso che abbiamo le formule per calcolare il potenziale, l’energia cinetica ed il Lavoro dobbiamo scoprire come queste si connettono fra di loro. Il modo più semplice per scoprire qual è la loro interconnessione è quello di studiare con occhio fisico la caduta della massa m da un’altezza h (vedi figura 6).
All’inizio , tutta l’energia è potenziale: Ui = m×g×h  ;  Ki=0

 Alla fine della caduta, ho tutta energia cinetica: UF=0  ;  KF = ½×m×VF2: la massa m ha guadagnato un’energia cinetica pari a m×g×h !
C’è stato ovviamente un trasferimento di energia da potenziale a cinetica. Il Lavoro, che come detto è la grandezza che descrive questo trasferimento. Calcoliamo il Lavoro eseguito: L=DP×F0 = h×Peso = h×(m×g) = m×g×h. Il Lavoro è proprio uguale al valore guadagnato dall’energia cinetica!
Se invece avessi lanciato la massa m dal suolo verso l’alto con la velocità iniziale VF essa sarebbe arrivata all’altezza h, fermandosi. Dunque: Ui=0 ; Ki= ½ ×m×VF2   ;    UF=m×g×h ; KF=0. In questo caso la massa m perde un’energia cinetica pari a -m×g×h ; il Lavoro in questo caso è: L= h(-m×g) = -m×g×h , che è proprio l’energia cinetica persa!
Possiamo generalizzare l’esempio della caduta a tutte le forze ed affermare che il Lavoro rappresenta l’energia trasferita in energia cinetica; quest’ultima aumenta se il Lavoro è positivo o decresce se esso è negativo. Messo in formule:

L = DK = KF – Ki                                        (12)     -sempre valida-
Tenete conto dell’eq. (12) perché è basilare per comprendere l’energetica di ogni macchina.
Se ho forze conservative, l’energia cinetica aumenta a spese di quella potenziale e viceversa, come già visto. Perciò vale sicuramente la relazione:
DU = - DK                                                    (13)              e di conseguenza:
L = -DU = -(UF – Ui) = Ui – UF            (14)   - se ho solo forze conservative-

 

COME AGISCE IL LAVORO?
Adesso che abbiamo in mano le formule essenziali… applichiamole! Vediamo con qualche semplice esempio come agisce il Lavoro.

Consideriamo una palla di massa 500g con velocità iniziale Vi=5m/s che si sposta per una distanza di 3m, spinta da una forza F0=2N. Voglio calcolare la velocità finale secondo i 5 casi di figura 7.

• F0 parallelo e concorde a DP (J=0)   ;   L = 2N×3m = 6J
•  F0 inclinato di 60° rispetto a DP        ;    L = F0//×3m = F0×cos(60°)×3m = 1N×3m = 3J    
• F0 perpendicolare a DP (J=90°)       ;   L = F0×cos(90°)×3m = 0N×3m = 0 
• F0 inclinato di 120° rispetto a DP      ;   L = F0×cos(120°)×3m = -1N×3J = -3J 
• F0 opposto a DP (J=180°)             ;   L = -2N×3m = -6J

Per tutti i casi vale l’eq. (12) e perciò scrivo:
L = KF – Ki ---> KF = Ki + L                      (15)
Per quanto riguarda Ki, essa risulta essere: Ki = ½×0,5kg×(5m/s)2= 6,25J.  Per quanto riguarda i 5 casi,  il Lavoro L lo abbiamo già calcolato. Usiamo l’eq. (15) ed otteniamo:

• 
• 
• 
• 
• 

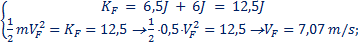
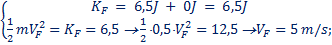
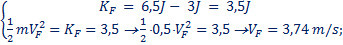
Nel caso c) la velocità rimane invariata perché non viene fatto alcun Lavoro –non viene trasferita alcuna energia cinetica (J = 90°)-.
Nei casi a) e b) la velocità aumenta perché il Lavoro trasferisce una quantità positiva di energia cinetica, in quanto F0 punta dalla stessa parte di DP (J < 90°).
Nei casi d) ed e) la velocità decresce perché il Lavoro trasferisce una quantità negativa di energia cinetica, in quanto F0 punta dalla parte opposta di DP (J > 90°).