LE INCERTEZZE NELLE MISURE DI LABORATORIO

MISURA DI UNA GRANDEZZA FISICA

 

Si definisce grandezza fisica di un sistema fisico una sua caratteristica sulla quali si possa eseguire un’operazione di misura. Misurare una grandezza fisica significa confrontarla con un’altra grandezza ad essa omogenea scelta come unità di misura. La misura indica quante volte l’unità di misura è contenuta nella grandezza misurata.

Es: una misura di lunghezza ha fornito il seguente valore:

L = 5.2 m

          

Il confronto di una grandezza fisica con l’unità di misura è reso particolarmente semplice ed immediato con l’utilizzo di strumenti di misura cioè apparecchi dove l’unità di misura è riprodotto su di essi e dove un indice (strumenti analogici) o un numero su un display (strumenti digitali) fornisce direttamente la misura. 

Def: Portata indica l’intervallo di misura entro cui lo strumento può operare. Se si usa uno strumento per misure superiori alla sua portata si rischia di rovinarlo !

Def:  Sensibilità è la più piccola variazione della grandezza che lo strumento permette di rilevare. Pertanto la sensibilità di uno strumento è la sua capacità a rispondere prontamente a variazioni della grandezza da misurare.

Nota: Normalmente portata e sensibilità sono caratteristiche contrastanti tra loro nel senso che  a strumenti di misura con grande portata corrisponde una scarsa sensibilità e viceversa.

 

INCERTEZZE NELLE MISURE

 

Esistono sempre degli errori associati alle misurazioni. C'è un'eccezione: se la misurazione consiste nel contare grandezze discrete cioè costituite di elementi separati, come il numero degli studenti in un laboratorio, allora il numero può essere esatto. Quando si parla di errore non si intende riferirsi ad uno sbaglio. Il significato tecnico di errore potrebbe essere descritto meglio con il termine incertezza. In qualsiasi misura di variabili continue, come la lunghezza, la massa, il tempo e così via, è inevitabile che ci sia incertezza nella determinazione del loro valore esatto. La miglior cosa che è possibile fare è fornire un particolare valore della misura, detto valore più attendibile o probabile Xp, con la garanzia che il valore  "vero" sia quello stesso numero, più o meno una certa quantità, chiamata errore assoluto o massimo DX. Allora, il risultato dell'esperimento viene dato nella forma:

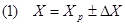
Errori sistematici e casuali. Si distinguono due tipi di errori: gli errori sistematici e gli errori casuali. Gli errori sistematici più comuni sono quelli dovuti al cattivo funzionamento della strumentazione utilizzata. Tali errori influiscono sul risultato di una misura sempre in un medesimo senso e portano o a misure in difetto o a misure in eccesso rispetto a quelle che si avrebbero in loro assenza. Se, ad esempio, un cronometro ritarda (va indietro) l'intervallo di tempo che si misura risulterà più breve di quanto esso non sia in realtà, la misura del tempo sarà allora errata per difetto. Oppure se in un righello costruito male il trattino usato per indicare il millimetro è minore del giusto si commetterà un errore per eccesso in tutte le misure di lunghezza eseguite. Gli errori sistematici una volta individuata la causa che li hanno provocati possono essere eliminati. Un'altra fonte di errore sistematico si ha quando lo strumento di misura interferisce con il funzionamento dell'apparato su cui si sta misurando una grandezza. Infatti questa è diversa con e senza strumento di misura applicato: è il caso delle misure di corrente e tensione con voltmetro e amperometro, perché con le loro resistenze interne cambiano la condizione di funzionamento del circuito in esame.
Gli errori casuali (detti anche accidentali) sono quelli dovuti all'operatore ed alle condizioni sperimentali della particolare misura. Questi errori modificano casualmente il risultato della misura o in eccesso o in difetto. Tali fluttuazioni sono dovute all’impossibilità di riprodurre esattamente in ciascuna operazione di misura le stesse condizioni sperimentali. Esempi di tali errori sono: errori di parallasse, errori di start e stop nella misura di intervalli di tempo, pulizia, deriva di strumenti con la temperatura etc. Con l'utilizzo di strumenti più sofisticati e con una maggior attenzione dello sperimentatore è possibile rendere gli errori accidentali piccoli ma, a differenza di quelli sistematici, non si possono eliminare del tutto.

Accuratezza e precisione. Per descrivere l’affidabilità delle misure si usano spesso i vocaboli accuratezza e precisione. La precisione indica il livello di reciproca vicinanza (concentrazione)delle misure ripetute. L’alta precisione riflette l’elevato livello di attenzione e perfezionamento nelle procedure e nella strumentazione seguite. L’accuratezza è la vicinanza di una misura al valore reale e pertanto comprende anche le deviazioni dovute ad errori sistematici non corretti.

 

Se ipotizziamo che il valore “vero” della nostra misura sia il centro del bersaglio della figura le misure accurate sono i tiri che arrivano vicino al centro. Se la distribuzione dei tiri è distribuita uniformemente attorno al centro del bersaglio gli errori sistematici sono piccoli. Gli errori sistematici sono evidenti quando i tiri sono “sistematicamente” fuori centro. Sebbene questo esempio illustra bene gli effetti dei due tipi di errori non si deve ignorare il fatto che quasi sempre nell’operazione di misura di una grandezza fisica non si conosce il valore vero. Quindi una migliore analogia con le misure reali la si otterrebbe togliendo i cerchi che mostrano la posizione del bersaglio. In tal caso risulta impossibile dedurre quale tiratore ha avuto gli errori sistematici più grandi. (vedi [1] pag. 96)

 

errore relativo. Nella pratica è più significativo, per poter stabilire la bontà o accuratezza di una misura, il concetto di errore relativo Er e di errore percentuale E%, invece che di quello assoluto DX (m,dX,s ), definiti come:

Da notare che, mentre l'errore assoluto ha la stessa unità di misura della grandezza misurata, l'errore relativo è adimensionale. E’ evidente che una misura è tanto più accurata quando più piccolo è l’errore relativo e percentuale. Se in una misura l’errore è dovuto solo alla lettura dello strumento, l’accuratezza cresce all’aumentare del valore della misura, perché l’errore assoluto resta invariato.

 

Errori nelle misure dirette- Cenni di statistica descrittiva

Si indichi con X una generica variabile aleatoria, cioè soggetta soltanto ad errori casuali, e si supponga di effettuare su di essa un numero N di misure, si possono presentare i seguenti casi:

1° Caso - Le misure effettuate danno lo stesso risultato, oppure si esegue una sola misurazione. Il valore più probabile  Xp è quello letto sullo strumento e l'incertezza è suggerita dalla sensibilità dello strumento; si parla pertanto di errore di sensibilità. Chiaramente l’errore di sensibilità è un errore massimo che assorbe tutti gli errori casuali.

Questo caso si presenta quando la misura è fatta con uno strumento poco sensibile. In tal caso è inutile eseguire più di una misura, tutte darebbero lo stesso risultato. Si pensi alla misura della larghezza di un foglio eseguita con un righello millimetrato. Con tale strumento l’errore di misura non è inferiore a 0.5 mm, corrispondente alla mezza divisione che l’operatore può apprezzare. Evidentemente l’errore di sensibilità è un errore massimo che assorbe tutti gli errori casuali.

2° Caso - Si eseguono alcune misure e queste danno valori che possono essere diversi tra di loro. Questo è il caso in cui la misura è eseguita con uno strumento sensibile.  Si definiscono:

def 1. La frequenza assoluta f è il numero di volte  che un valore o una classe di valori compare nelle misure effettuate.

E' ovvio che la somma di tutte le frequenze assolute corrisponde al numero complessivo delle misure eseguite.

def 2. La frequenza relativa fr è il rapporto tra la frequenza assoluta e il numero totale delle osservazioni.

Se il valore xk è stato misurato nk volte, la corrispondente frequenza relativa è frk=nk/N (che coincide con la probabilità P(xk) quando N è molto grande).

Ovviamente la somma di tutte le frequenze relative vale 1.

def 3.La frequenza percentuale f% è la fr moltiplicata per cento espressa in %.

Spesso si suddivide il campo di variazione delle misure  in un numero di intervalli di ampiezza costante Di e si raggruppano in classi di valori le misure ottenute che cadono in uno stesso intervallo. L’esito di questa operazione si rappresenta con un istogramma della distribuzione delle misure, cioè con dei rettangoli di base uguale alla larghezza dell'intervallo e di altezza uguale alla frequenza delle misure che cadono in quell'intervallo (Fig.1).

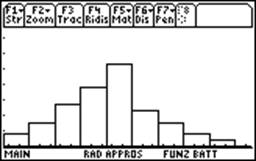
Fig.1 Istogramma delle misure del periodo di un pendolo per N=50.

 

I risultati delle misure non saranno distribuiti casualmente ma si collocheranno intorno a quello che “ragionevolmente” è il valore vero, o meglio, valore più probabile. La forma dell'istogramma suggerisce che tale valore è il valore medio o media di tutte le  N misure definita da:

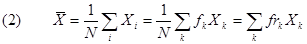
Una stima piuttosto pessimistica dell'errore assoluto è la semidispersione l definita come il valore assoluto della semidifferenza tra il valore massimo e il valore minimo fra quelli ottenuti:

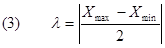
Prima della determinazione della semidispersione si deve fare una valutazione dei valori delle misure ricavate per eventualmente eliminare dalle misure concordanti quelle che si discostano notevolmente dalle altre, ad esempio, perché ottenute da una svista nell’eseguire le misure (errori grossolani).

Una miglior stima dell'errore assoluto può essere ottenuto in base alle seguenti considerazioni. La differenza fra la media e ciascuna misura Xi viene chiamata deviazione dalla media (o scarto o residuo):

Alcuni degli scarti sono positivi ed altri negativi dal momento che ci saranno degli Xi più grandi della media ed altri più piccoli. Questo implica che la media degli Di è zero, infatti:

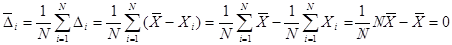
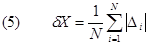Pertanto la media degli scarti non è un modo utile di caratterizzare l'incertezza della misura. Per evitare tale inconveniente si considera  il modulo degli scarti definendo deviazione media dXla seguente grandezza:

Dalla (5) si osserva che, al crescere del numero delle misure, dX  tende a diventare sempre minore: è questa è un'ulteriore conferma della necessità di eseguire una misura un gran numero di volte per ridurre al minimo l'errore dal quale essa è affetta. Pertanto il risultato delle N misure verrà indicato nella forma:

3° Caso - Sono accessibili grandi quantità di dati. E' evidente che, quanto maggiore è il numero N di misure acquisite tanto più grande è il numero di intervalli in cui si può suddividere il campo di variazione della X,  che raggiunge un  limite minimo  determinato dalla  risoluzione  del sistema di misurazione. L'istogramma delle misure tende allora ad appoggiarsi ad una curva continua di forma ben definita chiamata distribuzione limite. La distribuzione limite ha solitamente una forma simmetrica a "campana"  centrata attorno al valore medio di X. Un parametro utile per definire la larghezza della distribuzione e quindi anche dell'istogramma è la deviazione standard s definita come:

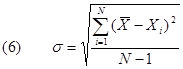
E' definita, inoltre, varianza la quantità:

Nella (6) e (6’) la somma dei quadrati degli scarti è divisa per N-1 e non per N come ci si dovrebbe attendere. In questo modo si vuole correggere una certa tendenza che si avrebbe, dividendo per N, a sottostimare la sparpagliamento delle misure, specialmente se il loro numero è piccolo. Questa tendenza è evidente nel caso estremo di N =1, cioè il caso in cui si effettui un’unica misurazione. In questo caso si avrebbe che il valore medio è l’unica misura effettuata e lo scarto sarebbe zero. La (6) darebbe il risultato indefinito s=0/0 che evidenzia la totale impossibilità di stabilire come siano distribuite le misure, mentre dividendo per N si avrebbe il risultato s=0 che è un’assurdità in quanto porterebbe alla conclusione che non vi sono errori nella misura.

Scrivendo l’esito di una misura nella forma:

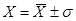
si intende dire che la probabilità che, ripetendo una singola misura, essa cada nell'intervallo

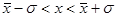
è del 68,3%, oppure che il 68.3 %. A rigore s rappresenta quindi non tanto l'incertezza media della distribuzione, ma quella delle singole misure.

 

Deviazione standard della media. Fra le N misure effettuate il valore medio è quello più affidabile e la sua deviazione dal valore vero è più piccola di quella delle N misure. Si può dimostrare che l'incertezza associata al valore medio è  volte più piccola di quella delle singole misure. Tale incertezza è chiamata deviazione standard della media  e vale (Taylor, pag. 150).

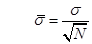
Perciò il risultato della serie di misure deve essere espresso nella forma:

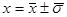
E’ importante sottolineare che poiché s rappresenta l’incertezza media delle singole misure, se facessimo alcune misure in più utilizzando la stessa strumentazione la s non cambierebbe apprezzabilmente. E’ più evidente il miglioramento della 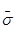cresce lentamente. In conclusione se si vuole migliorare decisamente la precisione è necessario cambiare la tecnica (cioè ridurre s) piuttosto che aumentare semplicemente N.

 

Approssimazioni dei valori numerici delle grandezze e cifre significative.

Nell’attività pratica è spesso necessario approssimare i risultati di una misura o, come spesso si usa dire, arrotondarli. Per fare ciò è necessario trascurare alcune cifre. Il numero di cifre da trascurare dipende da diversi fattori:

a) Dal grado di approssimazione che si vuole raggiungere. Il criterio di solito seguito nell’arrotondamento è che se la prima cifra da eliminare è minore di 5 le cifre rimanenti restano invariate (arrotondamento per difetto). Se le cifre da eliminare iniziano con un numero superiore o uguale a 5 si aumenta di un’unità la cifra precedente.
Si tenga presente che il numero di cifre significative del risultato di un’operazione di più misure deve essere uguale a quello della misura meno precisa.

Es 1: Supponiamo di sommare le tre masse 31.4 g + 2.36 g + 0.527 g. Il risultato fornito dalla calcolatrice è 34.287 g ma non tutte le cifre dopo la virgola hanno senso fisico poiché almeno una grandezza iniziale limita la sua precisione alla prima cifra dopo la virgola. La risposta corretta è quindi, arrotondando per eccesso, 34.3 g.

b) Dal grado di precisione con il quale la determinazione è stata effettuata, vale a dire dal numero delle cifre che hanno significato fisico (cifre significative). E’ quindi necessario distinguere in una misura le cifre significative da quelle non significative. L’importanza della significatività delle cifre è messa in luce dal seguente esempio.

La lunghezza di un campione misurata con un righello millimetrato è di 9,7 cm. Ciò significa che la lunghezza reale è compresa tra 9.6 e 9.8 cm. Pertanto la massa del campione dovrebbe esprimersi correttamente in (9,7±0.1)cm e non avrebbe senso scrivere 9.70 cm perché ciò avrebbe dovuto comportare l’uso di uno strumento  sensibile al centesimo di cm cioè (9,70±0.01)cm; in tal caso la misura assumerebbe una cifra significativa in più perché lo strumento è più sensibile.

E’ lecito assegnare agli errori statistici (media, deviazione standard) un valore di un ordine di grandezza migliore di quella dell’errore massimo (errore di sensibilità, semidispersione).

E’ ragionevole non indicare nella misura più cifre decimali di quante ne ha la sua incertezza. Si ha così la regola generale:

“L’ultima cifra significativa del risultato di una misura deve essere dello stesso ordine di grandezza dell’errore”.

Per questa ragione non è corretto dichiarare  per una misura di una lunghezza L=(3.045±0.02)m. La stessa misura è più ragionevolmente espressa da L=(3.05±0.02)m

 

Notazione scientifica, ordine di grandezza

 

In fisica spesso si incontrano grandezze le cui misure sono espresse da numeri molto grandi o molto piccoli. Per semplificare i calcoli tali numeri devono essere indicati con la notazione scientifica cioè come prodotto di una cifra compresa tra 1 e 10 per una potenza di 10.

 

Def: Ordine di grandezza di un numero è la potenza di dieci più vicina al valore numerico considerato.

 

Nota: se la parte non esponenziale del numero è superiore a 5, si deve arrotondare per eccesso all’ordine di grandezza successivo: così il numero 76536 = 7.6x104 ha ordine di grandezza 105.

 

Alcuni commenti generali sui grafici:

• Da qualche parte del grafico mettere sempre una didascalia, mesi più tardi nell'imminenza dell'esame ci si domanda ma che diagramma era ?

 

• Sugli assi vanno indicati i nome delle variabili e l'unità di misura impiegate.

• Scegliere la scala in modo che venga utilizzata la maggior porzione possibile del foglio per il grafico.

 

• Di fatto non esistono "punti" sul grafico poiché le misure sono affette da errori. Gli scarti derivanti da questi errori vanno rappresentati sul grafico riportando, con centro nel punto due segmentini uno orizzontale  e l’altro verticale di lunghezza pari al doppio dell’errore commesso. Le barre di errore in linea di principio sono su entrambi gli assi. Spesso avviene che la misura lungo un asse sia molto più precisa di quella lungo l'altro asse, per cui solitamente si indica una sola barra di errore.

• Se si vuole raccordare con una curva i dati riportati sul grafico farlo con una linea regolare. Infatti data la continuità dei fenomeni fisici si può ammettere che il legame fra la grandezza in ascisse e quella in ordinate sia in genere rappresentabile mediate una curva continua. A rappresentare i risultati si sceglierà quindi una curva che passi all’interno delle regioni individuate dai segmenti suddetti intorno ai punti rappresentativi delle misure. Le misure che non soddisfano a questo requisito vanno ri-verificate. Si noti che a volte è possibile tracciare diverse curve comprese nei limiti degli errori, in tal caso la conoscenza, in sede teorica, di una relazione tra le grandezze in esame è determinante per stabilire l’andamento della curva sperimentale.

 

Quando il grafico di una serie di dati ha un andamento regolare è possibile ricavare con buona attendibilità i valori di una grandezza anche in condizioni che non sono state sperimentate (interpolazione ed estrapolazione grafica).

 

ERRORI NELLE MISURE INDIRETTE- PROPAGAZIONE DEGLI ERRORI

Premessa. Se z = f (x,y) si chiama derivata totale di z rispetto a t la grandezza:

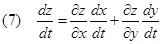
questa è anche la formula di derivazione delle funzioni composte.
Se nella (7) togliamo la dipendenza dalla variabile t si ottiene il differenziale totale dz

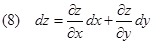
E’ noto infatti che il differenziale di una funzione rappresenta la sua variazione infinitesima per variazioni infinitesime delle variabili indipendenti x, y.

 

Errore massimo di una misura indiretta. Le misure dirette sono quelle misure effettuate con apparecchi tarati cioè determinate dal confronto diretto con una unità di misura presa come riferimento. Si considerino ora le misure indirette, cioè le misure di quelle grandezze ricavate attraverso relazioni analitiche in cui compaiono più misure dirette, cercando di valutare l’influenza degli errori con cui si conoscono le seconde, sugli errori con cui si conoscono le prime. Ad esempio per stimare lo spazio S percorso da un corpo che si muove di moto uniformemente accelerato possiamo misurare  la sua accelerazione a e il tempo t impiegato dal corpo a percorrere lo spazio s e poi usare la formula:

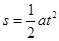
E’ chiaro che l’errore su S non può essere semplicemente la somma di Da e Dl  quanto questi hanno dimensioni diverse, tra loro!
Quindi, se la funzione  z = z (x1, x2, x3, …) dipende dalle misure x1, x2, x3, … ricavate con operazioni sperimentali ci domandiamo qual è l’incertezza con cui noi conosciamo z tenendo presente l’incertezza sulle misure x1, x2, x3, …?

Osserviamo il caso semplice dell’area di una superficie S rettangolare noti i suoi lati a e b e consideriamo come si propagano gli errori Δa e Δb. Essendo S=ab l’errore massimo ΔS che possiamo compiere su S sarà dato da:

S+ΔS=(a+Δa)(b+Δb)=ab+aΔb+bΔa+ΔaΔb

Se Δa è piccolo rispetto ad a e Δb è piccolo rispetto a b allora il prodotto ΔaΔb sarà piccolo
rispetto agli altri termini e lo possiamo trascurare. Fermandosi quindi a termini al primo ordine
possiamo scrivere:
ΔS=aΔb+bΔa
ora osserviamo che questo risultato, ottenuto in un caso particolarmente semplice, può essere
scritto anche:

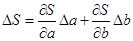
La relazione precedente altro non è che il differenziale totale di S, che per una funzione generica Z vale:

Se consideriamo che gli errori massimi delle grandezze dirette Dxi rappresentino piccole variazioni delle variabili indipendenti, allora possiamo stimare l’errore della grandezza derivata tramite il differenziale totale della funzione z = z (x1, x2, x3, …) sostituendo al posto di incrementi infinitesimi dx degli incrementi comunque piccoli ma finiti Dx.

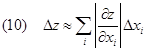
Si vede chiaramente che l'errore da cui è affetta una misura indiretta è sempre superiore a quelli di cui sono affette le misure fatte direttamente. Sarebbe quindi consigliabile procedere in modo diretto, ma spesso non esiste altra soluzione che il metodo indiretto.
La presenza del modulo nella relazione precedente è giustificato dal fatto che alla base della teoria degli errori, vi è la condizione per cui l’errore di una qualsiasi grandezza ricavata con misura indiretta, non può essere minore del più elevato tra gli errori delle grandezze componenti. In base a questa proprietà, anche se l’applicazione della (9) darebbe luogo a operazioni di differenza sugli errori, tali differenze vengono trasformate in somme (principio di additività degli errori). Quindi la (10) rappresenta il valore massimo dell’errore della grandezza z = z (x1, x2, x3, …).

La (10) ha un significato grafico diretto. Supponiamo per semplicità che z sia funzione di una
sola x, cioè z(x). Consideriamo una incertezza Dx fissata. Questa provoca una Dz diversa a
seconda che ci troviamo in una zona molto o poco ripida della curva z(x) cioè proprio a seconda
del valore della derivata .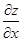
Con la (10) si è combinato l’effetto dei Dxi nel più pessimistico dei modi proprio per ottenere l’errore massimo possibile anche sulla misura di z; infatti può verificarsi una cancellazione parziale degli errori in xi. Quando le incertezze  Dx sono indipendenti e casuali , la somma della (10) può essere rimpiazzata da una somma in quadratura ottenendo una valutazione meno pessimistica per l’incertezza nel valore calcolato di z.

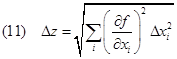
Nella (12) è stato sostituito l’errore assoluto Dx di ciascuna misura diretta con la deviazione standard s, ciò significa che se le misure xi sono governate da distribuzioni normali indipendenti, con deviazione standard sxi allora anche i valori z sono anch’essi distribuiti normalmente con deviazione standard data dalla (12).

 

Errore relativo nelle misure indirette. La definizione (1b) di errore relativo può essere rappresentata tramite il differenziale del logaritmo naturale della grandezza G:

Se G fosse una grandezza derivata legata alle grandezze dirette x,y,z…tramite una relazione costituita da prodotti di potenze:

In tal caso il calcolo dell’errore relativo risulta molto semplice:

 

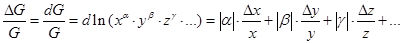
Es. La determinazione dell’accelerazione di gravità con il pendolo semplice. Valutiamo l’errore assoluto e relativo dell’accelerazione di gravità ottenuta con il pendolo semplice. Nella determinazione di g e in generale di misure di grandezze derivate è utile, in fase di progettazione della misura, fare un’analisi a priori degli errori relativi delle grandezze dirette in modo che essi siano bilanciati cioè siano dello stesso ordine di grandezza. Infatti una misura poco accurata vanificherebbe l’accuratezza di tutte le altre.

L’accelerazione di gravità g dipende dalle grandezze dirette, lunghezza L e periodo T, secondo la relazione funzionale: 

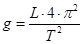
dalla quale otteniamo la formula per il calcolo dell’errore relativo di g:

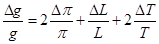
Il termine 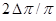può considerarsi trascurabile se il numero puro p è rappresentato con un numero di cifre significative elevato. E’ possibile stimare gli errori relativi di L e T considerando una lunghezza del pendolo di circa 1 m  e un periodo atteso di circa 2 secondi; l’errore assoluto nella misura di L e T è rispettivamente di 4 mm e di 1 centesimo di secondo. Quindi una stima “a priori” dell’errore relativo su g è:

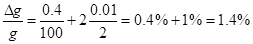
E’ evidente che il contributo all’errore relativo su L e T è sufficientemente bilanciato, la strumentazione è quindi adeguata. Come si vede il maggiore contributo all’errore deriva dalla misura di T per cui è consigliabile determinare il periodo con un numero adeguato di oscillazioni. Invece per la misura della lunghezza è inutile eseguire misurazioni di maggiore accuratezza.

Ipotizziamo ora che siano state ottenute le seguenti misure:

• lunghezza del pendolo……………….  L = (1.002 ± 0.004)m
• durata di 10 oscillazioni complete…… t  = (20.0 ± 0.2)s

 

Per la determinare dell’errore assoluto nella misura di g calcoliamo il periodo di oscillazione del pendolo in base ai dati assegnati: T = (2.00 ± 0.02) s

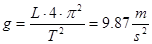
Differenziando, utilizzando la (10), ricaviamo l’errore assoluto:

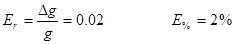Pertanto   g = (9.87 ± 0.24) m/s2

 

APPROFONDIMENTO: LA CURVA DI GAUSS

 

E’ stato osservato che se si effettuasse un numero infinito di misure e se il sistema di misura non presentasse limiti di risoluzione l’inviluppo dei rettangoli dell’istogramma tende a divenire una curva continua f(x) chiamata “distribuzione limite”.
La funzione di distribuzione tipica di un fenomeno complesso è la "distribuzione normale" o  "Gaussiana" la cui espressione matematica è:

Il coefficiente davanti all’esponenziale è detto coefficiente di normalizzazione. Il s è un parametro di larghezza della distribuzione e m ne è il valore atteso.
Il valore centrale m della distribuzione, che tende al valore vero della misura, è definito da:
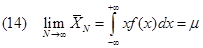che è equivalente alla (2).
Per dimostrare la (14) basta eseguire il cambiamento di variabili y = x-m   dy=dx    x= y+m, infatti  l’integrale diventa:

il primo integrale vale zero mentre il secondo è sÖ2p e pertanto si ha che il valore medio è m.

Analogamente il valore limite della varianza dopo molte misure è:

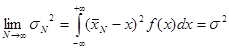
La deviazione standard ha il significato di “parametro di larghezza” della funzione di distribuzione. Essa è la metà della larghezza della funzione ad un’altezza pari a 0.607 dell’altezza massima della funzione stessa. Tale risultato lo si ottiene ponendo nella (13) x-m=s=1. Se si calcola la derivata seconda della (13) e la si pone uguale a zero è facile rendersi conto che la deviazione standard rappresenta l’ascissa del punto di flesso della funzione disegnata assumendo l’origine in m.

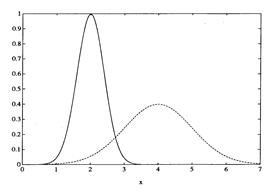
Fig.2 L’analisi della funzione di Gauss rivela che è una curva a campana simmetrica intorno a x = m. In m la curva ha il suo unico massimo, che è di altezza inversamente proporzionale alla larghezza s. Il grafico mostra due distribuzione gaussiane. Per la curva a tratto continuo m=2 e s=0.4, per la curva tratteggiata m=2 e s=1.

 

Nota. E’ stato detto che più misure vengono eseguite, più l’istogramma si avvicina alla distribuzione limite. Tuttavia normalmente neppure se si potessero ottenere infinite misure si arriverebbe ad un istogramma esattamente uguale alla distribuzione limite stessa. Per convincersi basti pensare al fatto che le densità di probabilità dei modelli teorici sono di solito infinitamente estese, cioè sono diverse da zero per qualunque valore di X, mentre le misure non possono ovviamente assumere qualunque valore. E’ impossibile che la misurazione della lunghezza dell’aula produca la misura “1m”, a meno che non sia intervenuto un grossolano sbaglio dell’operatore.

La distribuzione limite come densità di probabilità

La distribuzione limite f(x) è in realtà un’astrazione intellettuale, poiché non è possibile acquisire infinite misure. Il suo significato utile è quello di densità di probabilità, in modo che 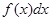 rappresenti la probabilità che una singola misura di X dia un risultato compreso in un intervallo largo dx centrato intorno a x.  In particolare, la probabilità che una singola misura cada in un dato intervallo [a,b], è data da:

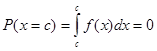Risulta, di conseguenza, che la probabilità che x prenda esattamente un valore c, qualunque sia c, è zero. Infatti:
Una interpretazione intuitiva del concetto di  densità di probabilità può essere ricavata nel modo seguente. Poiché:

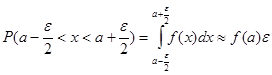
ne emerge che il valore f(a) della densità nel punto a è proporzionale alla probabilità che la variabile x prende un valore “vicino ad a”.
La probabilità per una misura di cadere in un punto qualunque di tutto l’asse è la certezza, quindi vale 1. Infatti:

La probabilità che una misura cada entro una deviazione standard è data dall’integrale:

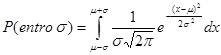
Ponendo y=(x-m)/s ® dx=sdy si ottiene:

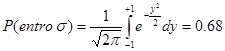
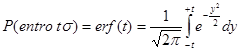Per un intervallo generico  m-ts<x<m+ts l’integrale diventa la error function erf(t) espressa da:

 

Il risultato di tale integrale non avendo soluzione analitica deve essere determinato al computer è:

Il grafico mostra che il 68% di un numero elevato di misure di una grandezza, presenta una deviazione inferiore a ±s; il 95,4 % delle misure ha un deviazione inferiore a ± 2s, mentre il 99.7 % delle misure ha una deviazione inferiore a ±3s. La statistica fornisce così un criterio per considerare non attendibili, e quindi da scartare, quei risultati che presentano una deviazione superiore a ± 3s: essi con ogni probabilità sono imputabili ad un errore sistematico, non rilevato, dell’operatore.

 

 Costruzione della funzione gaussiana da confrontare con un istogramma sperimentale.

Dai dati sperimentali raccolti si ricava il relativo istogramma. Il gruppo di dati sperimentali sarà buono se l’istogramma riproduce in modo accettabile la relativa curva di distribuzione teorica. E’ essenziale notare che in una serie ripetute un gran numero di volte nelle stesse condizioni, ciascuno degli eventi possibili si manifesta con la frequenza relativa fk che è, pressappoco, uguale alla sua probabilità Pk, cioè:

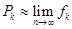
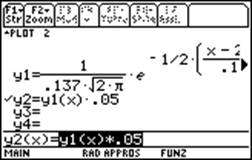
L’istogramma essendo una “curva di probabilità” dovrà essere confrontato non direttamente con la gaussiana f(x), che rappresenta una densità di probabilità ma con la relativa distribuzione di probabilità 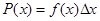 , dove Dx è la larghezza dei bin dell’istogramma. Si dovrà quindi calcolare il valore medio e la deviazione standard dei dati dell’istogramma e con essi determinare la gaussiana che dovrà essere poi moltiplicata per la larghezza del bin, come mostrato nella figura seguente.

E’ evidente che soltanto quando Dx = 1 la funzione di distribuzione coincide con la funzione di probabilità.

L’alternativa al procedimento sopra descritto  è quella di trasformare l’istogramma delle frequenze relative in un istogramma delle densità di frequenze dove per densità di frequenza si intende la frequenza di una classe divisa per la sua ampiezza (frequenza per unità di intervallino).

 

 

Le analisi di regressione

Eseguire un’analisi di regressione significa tracciare una curva che approssimi nel migliore dei modi l’andamento dei dati. Si individua così la tendenza del fenomeno e se la curva viene prolungata oltre i dati raccolti si entra nel campo delle previsioni.
Si consideri il caso che la relazione funzionale tra le grandezze x,y sia la retta 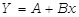. Si assuma che la variabile indipendente (X) è misurata senza errore o comunque abbia un errore trascurabile (è fissata dallo sperimentatore) e che ad ogni valore di X i dati Y seguono la distribuzione normale attorno al valore vero ed hanno la stessa varianza.

Procedura: metodo dei minimi quadrati (least squares) massimizza la gaussiana andando a ricercare la seguente condizione di minimo:

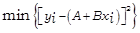
Il significato geometrico di questa espressione è chiaro: la retta, i cui parametri sono da determinare, è quella che rende minima la somma dei quadrati delle distanze, lungo la verticale, tra i punti sperimentali e la retta stessa. Tale retta è chiamata retta dei minimi quadrati o anche retta di regressione della variabile y sulla variabile x.

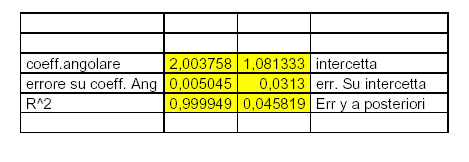
Con Excel. Selezionare un intervallo di 6 celle sul foglio di lavoro (3 righe e 2 colonne). Sul menu selezionare Inserisci e poi funzione, quindi scegliere statistiche dal menu a tendina e REGR.LIN. Inserire nella mascherina i valori delle Y, delle X e porre Cost:VERO, Stat:VERO. Per inserire la formula in modalità matriciale premere contemporaneamente i tasti Control+Maiuscole+Invio.

BIBLIOGRAFIA

• J.R.Taylor Introduzione all'analisi degli errori , Zanichelli, 2002.
• G.Cannelli Metodologie sperimentali in fisica, EdiSES, 2005.
• A.De Marchi, L.Lo Presti Incertezze di misura, Clut Editrice, 1993.
• E.Bava, R.Ottoboni, C.Svelto Principi di misura, Politecnico di Milano
• I.Bosco Trattamento delle misure nella scienza, Ed.Unicopli, 2003.
• M.Severi Introduzione alla esperimentazione fisica, Zanichelli, 1982.