Interazione delle radiazioni con la materia

     La caratteristica principale di una radiazione è il trasporto di energia, sottoforma di energia cinetica nel caso di particelle (cariche o no) o di energia di tipo elettromagnetico nel caso di fotoni.
Il principale effetto dell’interazione di queste radiazioni con la materia sarà la cessione di parte o di tutta l’energia alla materia, con possibile assorbimento della radiazione. Assorbimento che nel caso di particelle con massa ( tipo particelle α o particelle β ) significa riduzione ad uno stato di quiete all’interno del materiale, nel caso di fotoni la loro scomparsa.

Radiazione ionizzante e non ionizzante. E’consuetudine distinguere le radiazioni di tipo ionizzante, ossia quelle in grado di produrre ionizzazione degli atomi e delle molecole del mezzo attraversato, da quelle di tipo non-ionizzante, per le quali l’assorbimento è solamente in grado di creare una cessione di energia di tipo termico. In quest’ultima categoria rientrano ad esempio le radiazione di tipo ottico o ultravioletto, che come insegna la nostra esperienza sono in grado di produrre assorbimenti sotto forma termica. Le prime sono invece quelle in grado di provocare mutazioni a livello atomico e molecolare e sono perciò quelle più pericolose da un punto di vista biologico.
Un tipico valore per la ionizzazione atomica o molecolare è dell’ordine della decina di eV, valore che perciò costituisce in qualche modo l’energia discriminante tra i due tipi di radiazione.
Ionizzanti saranno quelle provenienti da decadimenti  α o β, mentre nel settore elettromagnetico saranno ionizzanti i fotoni a partire da frequenze del tipo X o γ. Tra le radiazioni ionizzanti, le prime sono dette direttamente ionizzanti in quanto il meccanismo di assorbimento implica una perdita di energia che coinvolge direttamente un numero elevato di ionizzazioni, mentre nel caso elettromagnetico si tratta di ionizzazione indiretta, perché mette in moto particelle a loro volta ionizzanti. A quest’ultima categoria appartengono anche le radiazioni neutroniche che vengono assorbite tramite reazioni di tipo nucleare.

     I meccanismi di interazione saranno comunque diversi a seconda del tipo di radiazione. Possiamo già anticipare che in base alla diversa efficienza di ionizzazione, diversa sarà la capacità di penetrazione delle diverse radiazioni, anche a parità di energia trasportata.

 

Avviene così che, nonostante la storia individuale di ciascuna particella carica sia diversa, il numero di urti e la strada percorsa nel materiale finiscano per essere molto simili tra loro. Questa situazione è completamente diversa da quella che descriveremo per i fotoni, per ciascuno dei quali il tragitto percorso è in generale diverso.
E’ così possibile per le particelle cariche di una certa energia definire un range (percorso) relativo ad ogni materiale. E’ importante notare che, ad una distanza un poco superiore al range, il fascio sarà completamente assorbito. Nella Fig.2 è mostrato un esperimento di trasmissione delle particelle alfa. Con I è indicato il numero di particelle alfa rilevate dopo che hanno attraversato un assorbitore di spessore t, mentre Io è il numero di particelle rilevate senza l’assorbitore. Dal grafico si osserva che gli assorbitori di piccolo spessore hanno soltanto l’effetto di diminuire l’energia delle particelle senza attenuare il numero di quelle che li attraversano. Aumentando via via lo spessore dell’assorbitore ad un certo punto inizia a diminuire il conteggio delle particelle e l’intensità del fascio tende rapidamente a zero.

Figura 2

 

 

 

La forte variazione del potere frenante durante l’assorbimento è alla base dell’utilizzo di particelle cariche pesanti (protoni, a, ioni più pesanti come 12C, 16 O o 20Ne) per terapia antitumorale. L’idea è quella di utilizzare il processo di cessione di energia e di ionizzazione per distruggere tessuti tumorali. È chiaro che questo non può avvenire a scapito degli altri tessuti vicini, e deve perciò implicare una cessione quanto più selettiva e localizzata dell’energia (ovvero della dose assorbita).
Sarà perciò necessario disporre di fasci di particelle con picchi di Bragg quanto più stretti possibile, con rapporto tra il picco e il plateau iniziale quanto più alto possibile. Si utilizzerà la variazione diretta con l’energia per calibrare l’energia del fascio in corrispondenza della distanza voluta.

 

Il percorso totale fatto dalla particella carica è però solo parte della storia. E’ utile e istruttivo caratterizzare il meccanismo di interazione introducendo il potere frenante lineare S (o in altra terminologia la perdita di energia specifica). E’ questo definito, al limite di piccoli intervalli, come il rapporto tra la perdita di energia (-DE, dove DE è la variazione di energia cinetica) e la distanza Dx su cui tale perdita si è avuta, ossia:

S = lim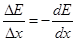  

Esso rappresenta pertanto, punto per punto, una misura dell’energia rilasciata localmente e di conseguenza del grado di ionizzazione in quel punto. La naturale unità di misura è l’elettronVolt al metro (eV/m), ma spesso viene più appropriatamente misurato in KeV/mm. Il potere frenante varia a seconda del materiale, della carica e dell’energia  iniziale della particella, ma soprattutto varia lungo la traiettoria durante il processo di arresto.

Il potere frenante lineare è ben descritto dalla formula di Bethe – Bloch

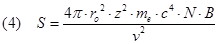
Dove r0 = e2/4Pe0mec2 è il Raggio classico dell’elettrone (2.81 x 10-15 m), z il numero di cariche della particella incidente (ad esempio z = 2 per una particella a), me la massa dell’elettrone, N la densità di atomi del materiale (atomi per unità di volume), v la velocità della particella e B il cosiddetto numero frenante dato da:

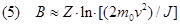
che è espresso in termini del numero atomico Z dell’assorbitore e dell’energia  media J di ionizzazione. La formula mette in evidenza che il potere frenante aumenta all’aumentare del numero atomico Z (perciò uno spessore di piombo è più efficace di uno di alluminio) e varia con maggior potenza con la carica della particella (a parità di altre condizioni, una particella a (Z = 2 ) è assorbita  quattro volte più di un protone  (Z = 1). Ma soprattutto importante è la dipendenza inversa dal quadrato della velocità della particella e quindi la sua dipendenza inversa dall’energia. Perciò il potere frenante aumenta al diminuire della velocità e sarà massimo proprio quando la particella sta per fermarsi. Perciò alla fine del percorso saranno massime la ionizzazione e l’energia trasferita.

Assorbimento di elettroni

 

Il quadro fin qui delineato per le particelle cariche pesanti viene in parte modificato nel caso di un fascio di elettroni, ottenuti ad esempio come prodotto di un decadimento b (Fig.6). Il motivo principale consiste nel fatto che la massa dell’elettrone incidente è uguale (e non enormemente più grande come nei casi precedenti) alla massa degli elettroni a cui viene a interagire.
Di conseguenza l’urto provoca in genere una deviazione della direzione dell’elettrone, e la traiettoria non è perciò in questo caso nemmeno approssimativamente rettilineo. I continui urti e i relativi cambi di direzione daranno origine ad un percorso tortuoso diverso elettrone per elettrone, con la conseguenza di non osservare in questo caso un picco di Bragg. Vi è anche la possibilità che alcuni elettroni possano a seguito dell’urto anche venire deviati all’indietro. Tutto questo implica che l’intensità del fascio, in funzione della penetrazione, non si annullerà in questo caso di colpo in un breve intervallo, ma in modo molto più diffuso.
L’effetto sarà anche maggiore nel caso in cui il fascio di elettroni, provenendo da un decadimento b, abbia già in partenza una certa distribuzione di energia e pertanto una più variabile capacità di penetrazione. Come mostra la figura 7 in cui le diverse intensità di fasci di elettroni sono graficate in funzione della penetrazione, è difficile definire in modo chiaro un range, ossia un percorso tipico caratteristico per tutti gli elettroni. In ogni caso, dato che a parità di energia la massa minore porta ad una velocità maggiore, la perdita di energia per unità di spessore sarà, minore che nel caso delle particelle pesanti. Diamo un valore tipico: per elettroni da 1 MeV, il range in aria è di 420 cm, nei tessuti molli di 0.5 cm, tutti i valori decisamente più grandi che nel caso delle a.

Figura 6

Figura 7

Da ultimo osserviamo che nel caso degli elettroni il processo di ionizzazione non costituisce l’unico meccanismo responsabile della perdita di energia. In questo caso diventa possibile (in alcuni casi, per alte energie o alti valori di numero atomico Z dell’assorbitore, decisamente competitivo) il processo di perdita di energia per emissione di radiazione elettromagnetica per frenamento. Si tratta del processo di tipo bremsstrahlung, che è fondamentale nella produzione di raggi X. Poiché la radiazione emessa non viene necessariamente assorbita (o non assorbita localmente), questa causa una possibile differenza tra potere frenante lineare S (legato alla perdita di energia) e il trasferimento lineare di energia LET (legato all’energia di fatto trasferita al materiale), che determina la ionizzazione specifica e la dose assorbita.

Assorbimento di fotoni

 

La perdita di energia dei fotoni della materia avviene principalmente attraverso tre meccanismi: l’assorbimento fotoelettrico, lo scattering Compton e la produzione di coppie. In tutti questi casi la dinamica della perdita di energia differisce decisamente dal comportamento graduale che si ha nel caso di particelle cariche. In questo caso il fotone subisce istantaneamente un evento che potremmo definire drammatico nella sua storia: viene infatti o completamente assorbito o deviato con perdita di energia e cambio di frequenza.
Nell’effetto fotoelettrico è coinvolto tutto l’atomo: in esso un fotone “colpisce” uno degli elettroni orbitali di un atomo del mezzo assorbente, cedendogli tutta la sua energia. A seguito dell’interazione il fotone scompare e l’atomo risulta ionizzato; l’elettrone colpito viene estratto dall’atomo e risulta animato da un’energia cinetica data da:

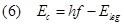
Dove Eg è l’energia di legame che unisce l’elettrone all’atomo.

 

Dalla fig.8 risulta evidente che l’interazione per effetto fotoelettrico ha una probabilità rapidamente decrescente con l’energia e risulta molto probabile per materiale assorbitore avente un numero atomico Z elevato. Tale effetto diventa quindi trascurabile per fotoni di energia superiore a pochi centinaia di KeV, mentre risulta l’effetto di interazione predominante al di sotto dei 100-150 KeV.

 

Nell’effetto Compton il fotone incidente non scompare dopo l’interazione, ma oltre all’elettrone estratto dall’atomo si ottiene un fotone diffuso di energia inferiore a quella iniziale, che viaggia su di una traiettoria diversa. La deflessione è tanto maggiore quanto più grande è l’energia ceduta nella interazione fino ad una deflessione massima di 180 gradi, ovvero alla retrodiffusione del fotone incidente; in tale situazione la formula (7) della pagina successiva fornisce il valore di energia ES del fotone diffuso in funzione dell’energia Ei del fotone iniziale, corrispondente alla cosiddetta spalla Compton dello spettro dei fotoni gamma (Fig.9).

 

L’interazione per effetto Compton risulta la più probabile nell’intervallo di energie dei fotoni fra le poche centinaia di keV e i pochi MeV.

Nella produzione di coppie un  fotone cede tutta la sua energia materializzandosi in un elettrone e ed un positrone, dotati di energia cinetica. La produzione di coppie è un effetto a soglia: poiché l’energia a riposo dell’elettrone e del positrone è uguale a 511 KeV, occorre che il fotone iniziale abbia una energia E > 1.022 MeV. Quanto più grande è l’energia, tanto maggiore è la probabilità dell’effetto; ad alter energie tale effetto diventa predominante rispetto agli altri.