Fisica pendoli accoppiati

PENDOLI ACCOPPIATI

 

5.1   Introduzione

Riteniamo che lo studio  del comportamento di un sistema di due pendoli che subiscono un'interazione reciproca debole e persistente, e che si dicono pertanto “accoppiati”, possa essere ragionevolmente proposto  anche a studenti della scuola media superiore per la vasta gamma di informazioni che se ne possono trarre.
L'analisi dei fenomeni di accoppiamento dovrebbe  collocarsi subito dopo l'affronto dei sistemi oscillanti semplici (pendolo semplice, pendolo fisico, molla), e potrebbe rappresentare una significativa introduzione al moto ondoso. La complessità del fenomeno fornisce la possibilità di differenti livelli di approccio: dalla semplice osservazione e descrizione qualitativa del fenomeno, tesa alla individuazione e all'analisi dei parametri significativi che lo influenzano, sino alla verifica delle legge che lo descrive.
Gli obiettivi dello studio di sistemi accoppiati potrebbero essere:

•  introdurre allo studio di un sistema fisico oscillante a due gradi di libertà
•  saper determinare empiricamente i modi normali di oscillazione di un sistema
•  saper interpretare un fenomeno periodico come sovrapposizione di oscillazioni

      armoniche distinte

•  saper riconoscere un esempio di battimento
•  saper cogliere analogie con altri fenomeni oscillanti

 

5.1   Studio di oscillatori accoppiati

 

Si considerino, due pendoli uguali (vedi Fig. 5.1)  realizzati con due aste rigide  collegate tra loro da una molla tenue e leggera, che, quando i pendoli sono all’equilibrio, non deve essere né compressa né tesa.  I due emboli A e B, attraverso due fori passanti, possano scorrere lungo le aste di sostegno  ed essere posizionati alla quota voluta.

 

Fig. 5.1 Pendoli accoppiati
Se i due pendoli sono liberi di oscillare solo su un piano, i gradi di libertà del sistema sono due. Per descriverlo sarà quindi necessario introdurre due variabili, che possono essere semplicemente le posizioni degli emboli in funzione del tempo t : xa (t) e xb (t).
L'equazione del moto può essere scritta nella forma:

m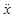a + kgxa + km(-xa + xb) = 0
e, per simmetria:                                                                                                    (5.1)

m b+ kgxb + km(-xa + xb) = 0

Dove nelle costanti km e kg abbiamo condensato rispettivamente le proprietà elastiche della molla e quelle “gravitazionali” dei due pendoli.
In generale il moto del sistema può essere molto complicato; è tuttavia possibile ricondurre il movimento dei due pendoli accoppiati alla sovrapposizione di due moti armonici semplici e indipendenti che si svolgono contemporaneamente.
Chiameremo questi moti armonici semplici modi normali di oscillazione.

In generale il moto di un sistema a più gradi di libertà oscillante liberamente si dice un modo normale se tutte le sue parti oscillano armonicamente con la stessa frequenza e la stessa fase iniziale, cioè attraversano tutte le posizioni di equilibrio allo stesso istante. In alter parole i modi normali sono i moti stazionari del sistema, i moti cioè che hanno caratteristiche costanti nel tempo. Un moto generico invece ha caratteristiche continuamente in evoluzione.

Quando è presente uno solo dei due modi normali, tutti i punti del sistema oscilleranno con la stessa pulsazione  w1. Si avrà quindi, considerando per i due pendoli una stessa ampiezza x0  e una stessa fase f1, che:

xa (t) = x0cos(w1t + f1)         e       xb (t) = x0cos(w1t +f1)           (5.2)

 

Se invece fosse presente solo il secondo dei due modi normali di oscillazione, tutti i punti  oscillerebbero con la stessa pulsazione  w2:

xa (t) =  x 0cos(w2t + f2)         e       xb (t) =  x0 cos(w2t + f2)           (5.3)

Il moto più generale di un sistema a due gradi di libertà è dato dalla sovrapposizione dei suoi due modi normali di oscillazione:

xa (t) =  x0cos(w1t + f1) + x 0cos(w2t + f2)        
(5.4)
xb (t) = x0cos(w1t + f1) + x0 cos(w2t + f2)           

I due modi normali di oscillazione e i parametri da cui dipendono, nel caso di due pendoli accoppiati, sono determinabili empiricamente con molta semplicità: spostiamo entrambi i pendoli nello stesso verso di una certa quantità xa = xb  (Fig. 5.2)

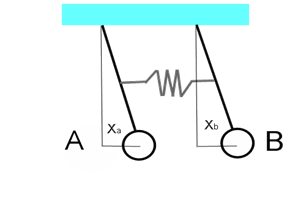
Fig. 5.2  Pendoli accoppiati in fase

In queste condizioni la molla, che non viene né compressa né tesa, non influenzerà il movimento dei due pendoli, che oscilleranno sincroni con una frequenza che dipenderà solo dalla forza di richiamo gravitazionale e sarà equivalente quindi alla frequenza delle oscillazioni libere dei due pendoli non accoppiati; le equazioni (5.1) diventano infatti:

m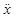b + kgxb  = 0                     (5.5)

con soluzione:                                            
w12  =  kg /m                                          (5.6)

Chiameremo questo modo di oscillazione primo modo normale di oscillazione.
Se invece spostiamo i pendoli di angoli uguali ma verso opposto (opposizione di fase, vedi Fig. 5.3)

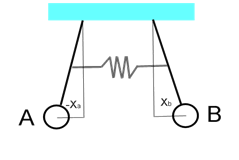
Fig. 5.3  Pendoli accoppiati in opposizione di fase

Si avrà che xb = - xa     da cui:       

m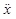a + kgxa + km(xa + xa) = 0
(5.7)
mb + kgxb + km(xa + xa) = 0

che daranno come soluzione: 

                                                                 w22  =  (kg + 2km)/m                                    (5.8)    

 

E' evidente che w2 >w1.
Alla luce di quanto appena visto, la soluzione generale, applicata ai pendoli che stiamo considerando,  prenderà una forma del tipo:

xa (t) =  x0 cos(w1t + f1)  + x 0cos(w2t + f2)    
(5.9)
xb (t) =  x0 cos(w1t + f)  -  x0cos(w2t + f2)   

Se per semplicità poniamo  f = f2= 0 otteniamo:

xa(t) = x0 cos (w1t)  + x0 cos (w2 t)
(5.10)
xb(t) = x0 cos (w1 t)  - x0 cos (w2 t)

Le velocità degli emboli sono ottenute derivando rispetto al tempo:

                                              va (t) =  - x0 w1sin(w1 t) -  x0 w2  sin (w2 t)
(5.11)
vb (t) = - x0 w1sin (w1 t) +  x0 w2  sin (w2 t)

All'istante t = 0 si ha che:

xA(0) = 2x0                      xB(0) = 0                 vA (0) = 0                   vB (0) = 0

Fig. 5.3 Pendoli in quadratura    

Si tenga cioè l'embolo A spostato di una certa quantità  2x0  mentre quello B in posizione di equilibrio e si lascino andare contemporaneamente.
L'esame sperimentale della condizione iniziale ricavata evidenza un fenomeno molto interessante che non possiamo non guardare con un senso di meraviglia: si osserva un alternarsi periodico della entrata in oscillazione di ciascun pendolo. Il pendolo A, in oscillazione, tramite le sollecitazioni della molla, mette in oscillazione il pendolo B. Ma il fenomeno non si arresta quando l'ampiezza delle oscillazioni di B eguaglia quelle di A (quando cioè l'energia iniziale è ugualmente ripartita tra i due pendoli): esso continua ad oscillare aumentando la propria ampiezza di oscillazione sino a quando il pendolo A si ferma per un istante. Dopo di che il fenomeno si ripete invertito: è come se l'energia inizialmente fornita a B oscillasse con frequenza regolare tra i due pendoli.
E' possibile verificare come la spettacolare configurazione che si ottiene rilasciando i pendoli in quadratura di fase, rappresenti una sorta di battimento (Fig. 5.4).
Se applichiamo infatti le classiche formule di prostaferesi alla soluzione generale (5.10) otteniamo:
xa (t) = 2x0 cos (w1  -  w2 )t/2   cos (w1  +  w2 )t/2
(5.12)
Xb (t) = -2x0 sin (w1  -  w2 )t/2   cos (w1  +  w2 )t/2

 

 

 

 

                                                                                                                                                            

 

 

 

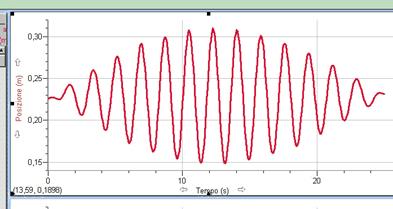
Fig. 5.4 Battimenti di un pendolo accoppiato

 

 

5.2   Poposta didattica per un esperimento con pendoli accoppiati

5.2.1  Prima fase: accordatura dei pendoli

Per semplicità ci sembra opportuno cominciare l'esperimento utilizzando due pendoli uguali sia dal punto di vista geometrico che fisico. Si chiede agli studenti di verificare che i pendoli, inizialmente non collegati,  oscillino con lo stesso periodo e la stessa frequenza. 
I pendoli utilizzati non sono in realtà dei pendoli semplici: una prima provocazione potrebbe essere quella di stimolare gli studenti a capire se l'utilizzo della formula che esprime il periodo dell'oscillazione di un pendolo semplice porta ad un errore significativo rispetto al grado di approssimazione che nell'esperimento si vuole ottenere. E' evidente che se le masse A e B sono consistenti rispetto alle aste, l'approssimazione di pendoli semplici è ragionevole. Se i due pendoli non avessero la stessa frequenza, li si “accorda” tramite piccoli spostamenti delle masse A e B. Ulteriore spunto di riflessione potrebbe derivare dalla richiesta che i pendoli siano “uguali”. Cosa significa “uguali” in fisica?

5.2.2  Seconda fase: accoppiamento

Creiamo quindi un collegamento elastico molto lasco, utilizzando uno spezzone di un sottile filo di acciaio armonico e fissandone gli estremi alla medesima quota alle aste dei due pendoli, in modo che all'equilibrio risulti piegato ad “U” senza modificare la direzione verticale dei pendoli.
Le compressioni e le trazioni della molla provocate dall’oscillazione di uno dei due pendoli, andrà a perturbare lo stato fisico dell’altro pendolo e viceversa, dando luogo così a configurazioni  che, nella loro semplicità, appaiono agli occhi dell’osservatore molto spettacolari.
Per valutare l’influenza di questa “molla” così semplicemente ottenuta, teniamo fermo in posizione verticale uno dei due pendoli e lasciamo oscillare soltanto l’altro; ci si rende subito conto che il periodo di oscillazione del pendolo  è diminuito rispetto a quello delle sue libere oscillazioni.
All’azione della forza di gravità si “somma” infatti il contributo elastico della molla, continuamente sollecitata durante le oscillazioni .
L’aumento della frequenza di oscillazione del pendolo – rispetto alla frequenza delle oscillazioni libere – sarà tanto più evidente quanto minore sarà la quota a cui fissiamo la molla (poiché la forza elastica è direttamente proporzionale allo spostamento, inciderà sul fenomeno anche l’altezza a cui verrà fissata la molla).

5.2.3  Terza fase: studio dei modi normali di oscillazione

Fatte le debite osservazioni sul contributo della molla, “liberiamo” anche l'altro pendolo.
E' forse opportuno accompagnare gli studenti alla “scoperta” dei due modi normali di oscillazione, di quelle configurazioni cioè che procurano, a tutti i punti del sistema, la stessa forza di richiamo per spostamento unitario e per massa unitaria (w2).
Una volta evidenziate le due pulsazioni w1   e   w2  caratterizzanti il sistema, può essere utile aiutare gli studenti a riflettere su quali siano i parametri fisici che le determinano, e alla intuizione  che la costante di accoppiamento, che dipende dalle caratteristiche della molla e dall'altezza a cui viene vincolata, stabilisce la “distanza” tra i modi normali di oscillazione.
Attraverso una serie di misure lo studente può essere invitato a verificare di persona il legame tra i due modi w1 e w2 di oscillazione e la frequenza di battimento.
Le misure dei periodi di battimento non sono semplici perché ciascun pendolo staziona per qualche frazione di secondo nella “zona” attorno alla quiete, rendendo difficoltosa la determinazione del preciso istante in cui si ferma. Non è solo per questo motivo che  l'utilizzo di sensori di movimento e l'immediata elaborazione grafica dei dati sperimentali attraverso un personal computer permette un'analisi più approfondita del fenomeno.
Se ci si trova di fronte a studenti particolarmente motivati si può anche proporre un'indagine sul comportamento del baricentro del sistema (trascurando, per semplicità, le aste dei pendoli).

 
5.2.4  Suggerimenti per ulteriori approfondimenti

Per una maggior completezza nello studio delle oscillazioni può essere interessante analizzare almeno da un punto di vista qualitativo come cambia il fenomeno se si utilizzano due pendoli diversi tra loro. Allo scopo è sufficiente spostare sensibilmente verso l’alto l’embolo di uno dei due pendoli, o addirittura sostituirlo con uno più pesante: quel che si evidenzia è che non ritroviamo più i battimenti.
Se modifichiamo strutturalmente uno dei due pendoli in modo da rendere sensibilmente differente i loro momenti di inerzia, le vibrazioni dell'uno possono non essere sufficienti ad innescare il movimento dell'altro. L'energia quindi, per propagarsi, richiede che i pendoli abbiano frequenze di oscillazioni comparabili.
Si possono  costruire altri sistemi fisici che presentano il fenomeno dei battimenti.

Due masse uguali vincolate a due molle verticali parallele, libere di oscillare e aventi la stessa costante di elasticità, siano collegate tra loro con un sottile filo di spago. Il filo permetterà così l’accoppiamento dei due sistemi che hanno la stessa frequenza di oscillazione (Fig 5.5). Per rendere evidente il fenomeno dei battimenti è opportuno organizzare le cose in modo che siano lunghi i periodi di oscillazione delle molle, e lasco (ma non troppo!) l’accoppiamento. Quest'ultimo può essere variato semplicemente utilizzando dei fili di collegamento di sezioni differenti.
Anche in questo dispositivo è semplice determinare i modi normali di oscillazione e la condizione di battimento.

 

 

 

 

          

 

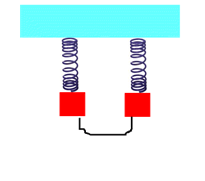
Fig. 5.5: Accoppiamento di molle oscillanti         

 

Se il classico sistema fisico molla verticale – pesetto  viene sospeso ad uno spezzone di filo, otteniamo un sistema a due gradi di libertà (Fig. 5.6). L'intero equipaggio può infatti oscillare verticalmente per la presenza della molla, o comportarsi come un qualsiasi pendolo galileiano grazie al contributo del filo. Il primo movimento dipenderà dalla rigidezza della molla e dal pesetto che vi abbiamo attaccato, mentre il secondo è determinato essenzialmente dalla lunghezza dell'apparato molla + filo. Variando la lunghezza del filo di sospensione varia il periodo delle oscillazioni pendolari.
Se si creano le condizioni affinché i due modi normali di oscillazione (quello verticale e quello pendolare) abbiano uguali frequenze si verifica un curioso ed inaspettato battimento.  Spostando dall'equilibrio la molla, tirando per esempio il pesetto verso il basso e successivamente rilasciandolo, l'elasticità della molla provoca oscillazioni verticali. Fino a qui nulla di inaspettato. In breve tempo però si innescano anche delle oscillazioni pendolari, che aumentano progressivamente di intensità a spese delle oscillazioni verticali che vanno esaurendosi, e viceversa. Quel che si manifesta è ancora un trasferimento periodico dell'energia da un grado di libertà del sistema all'altro. 

 

 

 

 

 

                                                          

 

Fig. 5.6: sistema molla - filo

Lo studio anche solo qualitativo di questi sistemi cosi apparentemente diversi tra loro, può portarci con naturalezza ad introdurre il moto ondoso come dovuto ad energia di natura meccanica che si propaga attraverso gli infiniti gradi di libertà di un sistema fisico.

 

5.3 Esempio di scheda studente*

Scopo dell'esperimento

Intendiamo studiare il comportamento di due pendoli collegati tra loro mediante una molla,  verificando in particolare secondo quali modalità avviene la trasmissione di energia tra i due sistemi oscillanti.

Materiale occorrente:   2 aste in alluminio 100 x 10 mm 2 anelli in PVC 30 x 100 x 30 2 cilindretti universali 26 x 24 x 10 2 traversini 50x20x10 4 viti con punta inox filo in acciaio armonico viti e dadi vari per il fissaggio dei componenti cronometro metro sistema di rivelazione con sonar personal computer

                       
Attività 1: costruzione e accordatura dei pendoli

Dopo  aver montato i due pendoli avendo come riferimento i prototipi già allestiti in laboratorio, devi verificare che siano accordati, che abbiano cioè la stessa frequenza di oscillazione libera. Per questo, senza operare il collegamento tra di due, dovrai eseguire delle misure dei loro periodi di oscillazione e confrontarli.
Non saranno mai perfettamente uguali; dal confronto dei dati dovrai decidere se ragionevolmente, tenendo conto degli errori sperimentali, potrai considerarli uguali.
Se non lo fossero cosa puoi fare per migliorare le cose?
I pendoli che hai costruito non sono due pendoli semplici. E’ ragionevole considerarli comunque semplici? Che errore si commette?

Attività 2: accoppiamento dei pendoli

Utilizzando uno spezzone di filo di acciaio armonico opera ora il collegamento tra i due pendoli e mettili in oscillazione. Cosa noti? In che modo la molla inserita influisce sul movimento dei due pendoli? Che forze si aggiungono nel momento in cui si genera l’accoppiamento? Quali sono secondo te i parametri che lo determinano?  Cosa accadrebbe se anziché il filo armonico utilizzassi un’asta rigida? E con un semplice filo di nylon?
Suggerimento: tieni fermo uno dei due pendoli e fai oscillare solo l’altro.
Cosa noti? La frequenza è ancora uguale alla frequenza delle oscillazioni libere? Perché si è modificata? All’equazione che esprime il moto di un pendolo semplice, quale termine dovrai aggiungere? Hai un’ipotesi di una nuova legge che esprima la pulsazione   del pendolo in questa condizione?

Attività 3: ricerca dei modi normali di oscillazione

Avrai notato la complessità del fenomeno che si genera quando metti in movimento i due pendoli.  Avrai forse osservato che il comportamento del sistema dipende molto dalle condizioni iniziali.
Quanti sono i gradi di libertà del sistema?
E’ noto ai fisici che se un sistema oscillante ha n gradi di libertà, devono esserci n condizioni in cui tutti i punti del sistema si muovono con stessa pulsazione w. Li cerchiamo? Hai un’idea di quali possano essere? Sapresti scrivere una formula che ti consenta di ricavare le pulsazioni di questi due modi particolari di oscillazioni che vengono chiamati dalla comunità scientifica “modi normali di oscillazione”?.
Se chiami w1 e w2 le pulsazioni dei modi normali, da quali fattori dipende il primo e da quali il secondo?  Come puoi “avvicinarne” o “distanziarne” i valori?

 

Attività 4: studio dei battimenti

Tra le diverse configurazioni iniziali senza ombra di dubbio la più interessante risulta quella che si ottiene mantenendo un pendolo in posizione di equilibrio e spostando l'altro di un certo angolo. Lasciando andare contemporaneamente i due pendoli rimarrai certamente meravigliato dal loro comportamento: prova a descrivere con parole tue quel che vedi accadere.
Ti trovi di fronte ad una sorta di battimento.
Con il sistema di acquisizione dati che hai a disposizione, costruisci i ralativi grafici (spazio-tempo, spazio-velocità, velocità-tempo) ed analizzali, cercando di confrontare i modi di oscillazione w1 e w2 e la frequenza di battimento.

• Bibliografia

 

• Franck – Crawford, Onde e oscillazioni (1972), Zanichelli.
• Fleury – Mathieu, Vibrazioni meccaniche – acustica (1967), Zanichelli.
• http://www.iapht.unito.it/stagefisica/pdf/Pendoli1.pdf
• http://www.ba.infn.it/~fisi2005/animazioni/simulazione006.html

 

* Questo semplice esempio è pensato per degli studenti che  frequentano il Laboratorio di Fisica Carlo Succi,  allestito presso il Dipartimento di Matematica dell'Università degli Studi di Milano.