Fisica quantistica

LA FISICA QUANTISTICA

Dalla seconda metà del XIX secolo la fisica pote­va dirsi assestata: la maggior parte dei fenomeni trovava spiegazione

• nella meccanica newtoniana,                    
• nella termodinamica

Alcuni fenomeni erano, tuttavia irrisolti:

1. la radiazione del corpo nero
2. l’effetto fotoelettrico (emissione di elet­troni da parte di metalli se irradiati da ra­diazioni di frequenza particolari)
3. la diffusione dei raggi X
4. il comportamento atomico

Negli anni compresi fra il 1895 ed il 1915 matu­rano molte delle scoperte e delle idee che hanno portato alla nascita della fisica quantistica  e della teoria della relatività:

1. Roentgen scoprì i raggi X nel 1895
2. J. J. Thomsom misurò il rapporto carica/massa dell'elettrone nel 1895
3. Bohr ridiscusse l'idea di atomo 1913
4. Planck, analizzando le proprietà dell'irrag­giamento termico introdusse il concetto di quanto di energia

• Becquerel scoprì la radioattività 1896

Fu così che nacque la fisica moderna, nel primo trentennio del XX secolo rappresentata dalla fisica quantistica, che studia il comportamento del mondo atomico e subatomico e dalla fisica della relatività, che si occupa dei sistemi a velocità dell’ordine di grandezza della luce.

La fisica moderna getta le basi per la comprensione della natura a livello atomico, modificando alcuni concetti della fisica classica ed introducendone di nuovi.
In particolare, la sua principale affermazione riguarda il comportamento duale della luce, sia come onda che come particella; simmetricamente, a livello microscopico, ogni particella ha in se un comportamento duale.
Ma non modifica la fisica classica per quanto riguarda il mondo macroscopico.

Ma andiamo per ordine

Spettro del corpo nero.
Un corpo nero non è necessariamente un corpo di colore nero; è un corpo in grado di assorbire tutta la radiazione e.m. che incide su di esso.
Il corpo nero ideale è anche un radiatore (emettitore) ideale, poiché ogni corpo emette le radiazioni che è in grado di assorbire (perciò emette tutte le radiazioni);
inoltre i corpi neri sono “radiatori” universali, perché, ad una data temperatura, presentano tutti lo stesso spettro di emissione in funzione delle frequenze (o delle lunghezze d'onda), indipendentemente dal materiale.

• Si noti che tutti i corpi caldi emettono onde em a causa della loro agitazione termica, dando origine ad uno spettro continuo le cui fre­quenze aumentano con la temperatura, spostando­si dall'IR all'UV Alla temperatura ambiente l'emissione termica è nel range dell'IR, quindi invisibile all'occhio uma­no;
• intorno ai 1000 K i corpi iniziano ad emettere luce rossa,
• poi arancione,
• poi verde e blu
• infi­ne si osserva la luminescenza bianca dei metalli incandescenti;
• oltre i 3000 K inizia l'emissione UV.

 

Una stella come il Sole, per esempio, può essere considerata con buona approssimazione un corpo nero. Essa assorbe la radiazione incidente senza rifletterla, ma allo stesso tempo emette luce propria.

Si ottiene un corpo nero utilizzando un blocco di metallo con una cavità accessibile solo tramite un piccolo foro: La radiazione em entra attraverso la fessura e continua ad essere riflessa dalle pareti con poca probabilità di uscire, finché viene completamente assorbita.
I fisici erano interessati a studiare il comportamento del corpo nero al variare della temperatura; per questo motivo il corpo nero è una fornace con le pareti annerite ed un piccolo foro di ingresso.

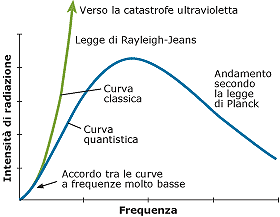
Studio della Radiazione del corpo nero
Semplici esperimenti di irraggiamento da parte del corpo nero hanno evidenziato la curva sperimentale a campana indicata in figura che indica l’Intensità di radiazione, proporzionale al numero di “fotoni” presenti nella cavità, in funzione della frequenza della radiazione em;
curva completamente diversa da quella deducibile dalle leggi della fisica classica e soprannominata “catastrofe ultravioletta”.

• Si scalda il corpo nero fino ad una determinata temperatura di riferimento T1 che rimane poi costante
• Si misura la quantità di radiazione e.m. emessa dal corpo nero al variare della frequenza
• Il grafico dell’intensità di radiazione in funzione della frequenza ha un caratteristico andamento a “campana”. L’area sottesa misura l’energia totale emessa dal corpo nero.
• Variando la temperatura di riferimento T2 e ripetendo l’esperienza al variare delle stesse frequenze si ottiene sempre una curva a campana, ma diversa e non sovrapponibile alla prima.
• Alle basse frequenze si ha poca radiazione
• Alle frequenze intermedie si osserva un picco di emissione
• Alle alte frequenze si ha di nuovo poca radiazione
• Al crescere della temperatura di riferimento T aumenta l’area sottesa dal grafico, ossia un corpo caldo irraggia più energia di uno freddo
• Al crescere della temperatura di riferimento T il picco di emissione e si sposta verso le frequenze più alte
• Il picco della curva segue la legge di Wien:

 

f picco = 5,88 1010 T
λpicco = c/fpicco
e la legge di Stefan – Boltzmann:                    
I = σT4

l'energia irradiata I, per unità di superficie ed unità di tempo è proporzionale alla quarta potenza della temperatura assoluta. La costante di Boltzmann è σ = 5,7 10-8 W(m2K4)

• L’andamento della distribuzione della radiazione del corpo nero NON dipende dal materiale: una fornace di acciaio ed una di rame, alla stessa temperatura di riferimento T, danno la stessa curva a campana (sovrapponibili)

Spettro del corpo nero e Crisi della fisica classica

La fisica classica osservò che il campo em poteva scambiare energia con gli atomi di un corpo.
Ad esempio: un corpo si riscalda perché assorbe radiazione em, oppure la radiazione em assorbita può generare reazioni chimiche.
La fisica classica, inoltre, non poneva nessun limite all’energia elettromagnetica che un corpo può assorbire ed emettere: un corpo può assorbire energia di qualunque frequenza con continuità, raggiungen­do valori elevatissimi nell'intervallo dell'UV, ma la catastrofe UV, non si verificava. L’andamento “finito” dello spettro di emissione del corpo nero evidenziava un limite al valore dell’energia scambiata fra corpo nero e radiazione em., limite che cresce con la frequenza, ma che non può essere superato.

I quanti di Planck.
Il fisico tedesco Planck, nel 1899, formulò una teoria rivoluzionaria che gli valse il premio Nobel nel 1918.
Egli ipotizzò che gli scambi di energia fra gli atomi del metallo e la radiazione em avvengano a “pacchetti”, che definisce “quanti di energia” proporzionali alla frequenza dell'onda incidente;
se f è la frequenza della radiazione em incidente, l’energia E che può essere scambiata con il corpo nero è un multiplo intero della la frequenza f :
E = hf
h = 6,6310-34 Js
h è la costante di Planck, considerata ormai una delle costanti fondamentali della natura.
Questa ipotesi comporta che l’energia è quantizzata (come la carica elettrica) e non può assumere tutti i valori; può assumere solo valori discreti e può variare per salti quantizzati molto piccoli, come si vede dal valore di h.
Con queste nuove basi, Planck trova una spiegazione allo spettro del corpo nero ed una formulazione matematica che lo spiega; infatti rifacendo i conti teorici in base alla sua nuova ipotesi, Planck ottiene una curva che ripro­duce esattamente i dati sperimentali, scongiura la catastrofe uv, introdusse la natura corpuscolare della luce.

• Più è grande la frequenza maggiore è il quanto di energia
• Al crescere della frequenza, cresce anche l’energia necessaria per il più piccolo salto quantico
• Il corpo nero ha una quantità finita di energia e non può fornire l’energia necessaria ad un salto quantico alle alte frequenze; non potendo fare il salto la radiazione si annulla alle alte frequenze.

Lo stesso Planck non era però soddisfatto e pensava di avere costruito un espediente matematico ad hoc  utile per spiegare il fenomeno “corpo nero”.
Ma ogni dubbio cadde grazie ad Einstein e all’effetto fotoelettrico. Einstein fu l’unico a prendere sul serio la teoria dei quanti di Planck e, addirittura l’applicò alla luce, affermando che:

• La luce (radiazione em) viaggia in pacchetti di energia.
• Una luce di frequenza f è formata da fotoni di energia quantizzata: E = hf., proporzionale ad f
• Il fascio di luce può essere pensato come un fascio di particelle, ognuna di energia E = hf.
• Al crescere dell’intensità del fascio cresce il numero n di fotoni (particelle) che attraversano lo spazio in un secondo.
• Il numero di fotoni è proporzionale all’intensità della radiazione luminosa
• L’energia di un fotone visibile è dell’ordine dell’eV.

 

Effetto fotoelettrico.

L'effetto fotoelettrico consiste nell'emissione di elettroni da parte di una superficie metallica (specie alcalina) solo quando viene colpita da radiazione em di frequen­za opportuna.

L’effetto fotoelettrico fu osservato, inconsapevol­mente, da Hertz, deve il suo nome a Righi, valse il Premio Nobel sia a Lenard (1905) perché lo studiò che ad Einstein (1921) perché lo interpretò. Infine, aprì la discussione sia sull’esistenza o meno dei quanti di luce, introdotti per la prima volta da Plank, per spiegare il comportamento del corpo nero, che alla duplice natura della luce.

Nel 1887 Heirich Hertz dimostra sperimental­mente sia l’esistenza delle onde elettromagneti­che, sia che la loro velocità è uguale a quella della luce (c ≈ 3,0*108 m/s), conferendo, così, validità alla teoria elettromagnetica di Maxwell.
Inoltre nota che alcuni metalli esposti a radiazio­ne em si scaricano, cioè perdono elettroni.
L’anno successivo, Augusto Righi osserva, inve­ce, che sottoponendo a radiazione ultravioletta due elettrodi nasce un arco voltaico, ossia gli elet­troni di conduzione del metallo acquistano ener­gia sufficiente per vincere l'attrazione del reticolo ed uscire dal metallo; battezza tale fenomeno ef­fetto fotoelettrico.
Nel 1899, quattro anni dopo la scoperta dell'elet­trone ad opera di Thomson, gli scienziati ipotiz­zano che le particelle emesse dai metalli colpiti dalla radiazione em siano proprio gli elettroni.

Thomson e successivamente Lenard, eseguono esperimenti sul fenomeno fotoelettrico, e scopro­no che

1. le condizioni di emissione degli elettroni da parte dei metalli variano da metallo a metallo
2. l’intensità luminosa può aumentare senza produrre aumento nell’energia con cui gli elettroni fuoriescono
3. ogni metallo ha  una propria  frequenza caratteristica fsoglia
4. se la radiazione incidente è di frequenza inferiore  alla fsoglia non si osserva nessuna emissione elettronica.

Ad esempio la  fsoglia di zinco e magnesio è nel­l’UV, quella del sodio nella zona del visibile.

Questi aspetti dell'effetto fotoelettrico risultavano incomprensibili alla fisica classica e furono spie­gati  in via teorica da Einstein utilizzando la teo­ria dei quanti; successivamente Millikan verificò sperimentalmente le ipotesi di Einstein utilizzan­do una fotocellula (circuito contenuto in un tubo a vuoto formato da un  generatore ed un reostato).

• Un’ampolla d quarzo vuotata d’aria contiene due elettrodi:
• il fotocatodo illuminato con radiazione em di frequenza f nota emette elettroni
• la seconda placca li raccoglie
• la corrente di elettroni (= corrente fotoelettrica) che si sposta dal fotocatodo alla placca è misurata da un galvanometro
• se la placca è portata ad un potenziale negativo Vplacca < 0 gli elettroni non possono raggiungerla e la corrente si annulla.
• L'andamento della corrente fotoelettrica ha per­messo di interpretare l'effetto fotoelettrico e l'andamento grafico dell'energia dell'elettrone in funzione della frequenza è dato da una retta,
• la cui intersezione con l'asse della frequenza (ascissa) rappresenta il valore della frequenza di soglia
• la cui pendenza rappresenta la costante di Planck

L’esperienza ha mostrato le caratteristiche dell’effetto fotoelettrico

• L’emissione dei fotoelettroni è istantanea
• Ogni metallo presenta una frequenza caratteristica detta frequenza di soglia f sofglia = f0
• Si ha emissione di fotoelettroni solo se la radiazione incidente  ha una frequenza maggiore di quella di soglia
• Se la luce ha frequenza inferiore a quella di soglia non si ha assolutamente emissione di fotoelettroni
• L’emissione di fotoelettroni NON dipende dalla intensità della luce (dal numero di fotoni che compongono il fascio)
• Se la luce ha frequenza maggiore di quella di soglia e quindi provoca fotoemissione, all’aumentare dell’intensità cresce il numero di fotoelettroni emessi
• i “fotoelettroni” che fuoriescono dal metallo hanno energia cinetica; il valore dell'energia cinetica dipende dalla frequenza della radia­zione elettromagnetica incidente e non dalla sua intensità
• il valore dell'energia cinetica dipende SOLO dalla frequenza della radia­zione elettromagnetica incidente e non dalla sua intensità
• il numero di fotoelettroni emessi dipende dall’intensità della radiazio­ne  elettromagnetica incidente.

Effetto fotoelettrico e Crisi della fisica classica

La soglia fotoelettrica non è spiegabile con la fisica classica: un elettrone fuoriesce se si fornisce un’energia uguale al lavoro di estrazione Lestrazione (= numericamente uguale al potenziale intrinseco, ma espresso in eV), caratteristico di ogni metallo. L’energia è fornita dalla componente elettrica della radiazione em, che accelera l’elettrone aumentandone l’energia cinetica;
la componente elettrica cresce con l’intensità della radiazione em e aumentando l’intensità  (non la frequenza) l’elettrone dovrebbe aumentare la propria energia, rompere il legame con il reticolo ed andare in conduzione. Ma ciò non acccade, Al contrario ogni metallo presenta una frequenza di radiazione ben definita per poter emettere elettroni e l'emis­sione è immediata (avviene alla velocità della luce c).

Einstein spiega l’effetto fotoelettrico
Einstein assume che la radiazione em scambia energia con il metallo in modo discontinuo, cioè discreto, assorbendo singoli fotoni (1, 2,... mai 1/, 2/3..di fotone).
Il fotone di energia E =hf incide sul metallo, interagisce con un singolo elettrone e viene assorbito. Il fotone scompare e l’energia dell’elettrone aumenta della quantità E=hf.
L'elettrone, però, sfugge al reticolo metallico solo se acquista un'energia uguale o superiore al lavo­ro di estrazione Lestrazione.
Si ha quindi la condizione Lestrazione = h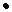fsoglia da cui si ottiene   
fsoglia =

se fincidente < f soglia l'energia che il fotone co­munica all'elettrone nell'urto è minore del lavoro di estrazione e non produce foto-emissione ma un aumento della temperatura del reticolo.
Se fincidente = > f soglia, l'elettrone assorbe dal fotone energia uguale o maggiore a quella di estrazione e fuoriesce dal metallo.
L'eventuale surplus di energia rappresenta l'energia cinetica con cui l'elettrone si allontana.

Ecin = h∙ fincidente – Lestrazione.

Per la spiegazione dell'effetto fotoelettrico Ein­stein ottenne il premio Nobel nel 1921.
Ricordando la relazione c=λ∙f, è facile dedurre la lunghezza d’onda di soglia per l’effetto fotoelettrico.

L’effetto fotoelettrico e la natura della luce.
L'interpretazione dell'effetto fotoelettrico con la conseguente accettazione della teoria dei quanti di Planck mette in luce la natura corpuscolare e non ondulatoria (Maxwell) della luce: i fotoni di luce sono visti come “proiettili” che colpiscono l'elettrone cedendo energia (urto elastico) ed in moto con quantità di moto
p =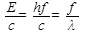

Da qui si fa strada l’idea della doppia natura della luce. Questa ipotesi non deve stupire.
Infatti anche l’uomo si comporta da figlio, marito, padre, uomo d’affari a seconda delle circostanze e dell’ambiente: non si comporta da marito con un cliente, eppure nessuno si stupisce di ciò.
Quindi la luce manifesta proprietà corpuscolari o ondulatorie a seconda della situazione in cui si trova.

Born dirà che gli esperimenti volti a provare la natura ondulatoria della luce non possono in nessun modo mettere in evidenza la sua natura corpuscolare e viceversa, sostenendo questa affer­mazione nel principio di complementarietà.

Applicazione dell'effetto fotoelettrico.
La tecnologia di uso quotidiano utilizza larga­mente l’effetto fotoelettrico, di cui siamo “incon­sapevoli” spettatori ogni volta che prendiamo l’a­scensore ed osserviamo il funzionamento a scorri­mento delle sue porte. Un raggio luminoso, infat­ti, attraversa lo specchio della porta aperta; lo stesso raggio luminoso colpisce una cellula fotoe­lettrica per produrre elettroni che attivano il cir­cuito elettrico di chiusura della porta. Il raggio lu­minoso viene interrotto dal nostro passaggio; in questo modo si interrompe la corrente elettrica, così da impedire che la porta si richiuda.
Gli impieghi sono molteplici e vanno dai disposi­tivi d'allarme agli automatismi per cancelli o por­te, inoltre i cronometri di molte discipline sporti­ve sono collegati a fotocellule. Le cellule fotoe­lettriche possono comandare l'accensione di lam­pade a seconda della luminosità presente, negli anni 60 alcuni costruttori di televisori impiegava­no una fotocellula per adeguare la luminosità del­l'immagine in bianco e nero, alla luminosità del­l'ambiente.

I fotoni e le nuove formule fisiche.
Il termine fotone è stato usato per la prima volta nel 1926 da Lewis ed identifica una particella di luce; tuttavia differisce dalle comuni particelle.
Le particelle classiche si possono toccare e pesare perchè dotate di massa.
Il fotone si muove alla velocità della luce

uguale per tutti gli osservatori e non può essere toccato, non può essere raggiunto e non può essere pesato poiché ha massa a riposo nulla. non decade spontaneamente ed ha vita media infinita.
La sua massa a riposo è nulla, ma ha energia a riposo E0 = mc2

La sua energia E, è:

oppure
E=hf

dove k è il vettore d'onda di modulo k = 2π/λ, ω = 2πν la frequenza angolare e ħ = h/2π la costante di Planck ridotta.
Nonostante la massa a riposo sia nulla, è possibile definire una massa equivalente a partire dalla relazione di Einstein E=mc² che risulta essere pari a

• Astronavi a vele di luce: le navi trasferiscono la quantità di moto dei fotoni dal Sole alla nave; la vela riflette i fotoni e crea variazione della quantità di moto ed una forza di reazione sulla vela dovuta alla pressione di irraggiamento dei fotoni.

 

L'effetto Compton.
L'effetto Comptom porta alla completa accettazione della teoria della quantizzazione dell'energia e conferma la natura corpuscolare della luce.

Dopo l'interruzione causata dalla prima guerra mondiale, nel 1923, Arthur Compton conferma sperimentalmente la natura corpuscolare della ra­diazione em, studiando la diffusione dei raggi X da parte di un campione di grafite: i raggi X deviati dagli elettroni della grafite variano la lunghezza d'onda (fre­quenza), assumendo

λfinale >  λincidente.
f finale  < f incidente

il fotone diffuso ha un’energia inferiore di quello incidente

Effetto Compton e Crisi della fisica classica
Come per l'effetto fotoelettrico e per il corpo nero, questo risultato è incomprensibile sulla base delle leggi della teoria ondulatoria classica della luce, secondo la quale i raggi X incidenti dovreb­bero essere diffusi in tutte le direzioni, con la me­desima lunghezza d'onda, contrariamente ai risul­tati sperimentali.
Secondo la fisica classica la radiazione X colpisce un elettrone fermo e libero da legami mettendolo in oscillazione alla sua stessa frequenza; l’elettrone, a sua volta, irradia una radiazione em della stessa frequenza incidente, comportandosi come un circuito oscillante/antenna.

 

Compton dimostra la natura corpuscolare della luce.

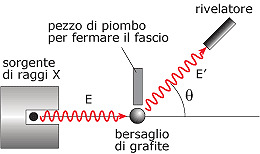
Considerando la radiazione come un corpuscolo, dotato di energia e di quantità di moto, Compton studia l'interazione tra fotone (radiazione X) – elettrone (del reticolo di grafite) come un urto elastico ed applica le leggi di conservazione dell'energia e della quantità di moto in forma rela­tivistica (a causa delle velocità coinvolte); ottiene, così, una relazione che esprime la variazione di lunghezza d'onda dei raggi X in funzione dell'an­golo di deviazione del fascio incidente.


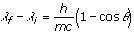
dove h è la costante di Planck,
m è la massa dell'elettrone
c è la velocità della luce.

• Se il fotone rimbalza indietro, angolo = 180° e si ha la massima variazione di λ.
• Se il fotone attraverso la grafite con angolo = 0°, invece, non si ha variazione di λ

 

Con                 λ Compton. = h/mc =

Storicamente l'effetto Compton è importante per­ché convinse in maniera pressoché definitiva la comunità scientifica che la radiazione elettroma­gnetica possiede una natura corpuscolare

 

Formule:

• conservazione dell’energia:                 

hf1= hf2 + E cin,elettrone

• conservazione della quantità di moto    lungo x

 hf1/c = hf2 /c cosθ + p elettrone cosφ

oppure

h/λ1=  h/λ2 cosθ + p elettrone cosφ

• conservazione della quantità di moto lungo y   

0 = hf2/c sinθ + p elettrone sinφ

0 =  hc/λ2 sinθ + p elettrone sinφ

si ottiene la variazione della lunghezza d'onda del fotone per effetto della diffusione:

Crisi del modello atomico classico.
Secondo il modello “planetario” di Rutheford, gli elettroni dovrebbero cadere sul nucleo in circa un centesimo di microsecondo ed emettere radiazioni con spettro continuo, in contraddizione con i dati sperimentali, cioè

• la luce emessa dal sole e da una lampada ad incandescenza presenta uno spettro di emissione continuo
• la luce emessa da una lampada a gas (idrogeno, mercurio,..) presenta uno spet­tro a righe; le righe corrispondono a ben determinate frequenze.

Per superare le contraddizioni legate al modello di Rutheford, Niel Bohr utilizza la teoria quantisti­ca avanzando le seguenti ipotesi:

• in un atomo gli elettroni ruotano solo in particolari orbite circolari stabili dove non emettono energia
• ad ogni orbita corrispondente un ben defi­nito valore di energia
• se l'elettrone scende da un'orbita permessa di energia maggiore ad un'orbita di ener­gia minore emette energia, rilasciandola sotto forma di fotone (quanto di energia)
• se l'elettrone sale da un'orbita permessa di energia minore ad un'orbita di energia maggiore assorbe energia dal fotone che lo colpisce

in base a queste ipotesi, Bohr assume che gli ato­mi hanno livelli energetici discreti di cui occupa­no il più basso, detto livello fondamentale. Per sa­lire ai livelli superiori, detti eccitati, deve assorbi­re energia dal fotone di frequenza
f =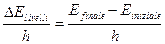

Altri esponenti della fisica quantistica.

Louis De Broglie e l'unificazione onda – corpu­scolo.
La teoria dei quanti di energia di Planck consoli­dava la duplice natura (onda-corpuscolo) della ra­diazione em e rivela il comportamento ondulatorio o corpuscolare a seconda dell'esperi­mento e dl fenomeno studiato.
Nel 1924 il francese Louis De Broglie suggerisce di estendere a tutti i corpi, anche materiali, la du­plice natura (corpuscolare e ondulatoria) già os­servata per la radiazione elettromagnetica e di as­sociare a ogni particella un'onda, detta onda di materia, di lunghezza d'onda
λ =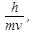

dove m è la massa della particella e v la sua velo­cità, h la costante di Planck

L'ipotesi di De Broglie venne confermata nel 1927 dai risultati di una serie di esperimenti di in­terazione elettrone-cristallo condotti dai fisici sta­tunitensi Clinton Joseph Davisson e Lester Hal­bert Germer, oltre che dal fisico britannico Geor­ge Paget Thomson.

Wolfgang Pauli e la comprensione della tavola periodica
Nel 1925 il fisico austriaco Wolfgang Pauli enun­cia il principio di esclusione che stabilisce un li­mite per il numero di elettroni che possono occu­pare un determinato livello energetico; trovano così giustificazione le diverse proprietà dei singo­li elementi chimici e si inizia a comprendere la struttura della tavola periodica.

Werner Heisenberg ed un limite alle misure microscopiche.
Nel 1927 Heisenberg formula il principio di inde­terminazione, con il quale viene riconosciuta l'e­sistenza di un limite naturale alla precisione con cui si possono misurare simultaneamente alcune coppie di grandezze fisiche, quali ad esempio po­sizione e quantità di moto ed energia e tempo.
Avvalorando l'ipotesi di  De Broglie, se una parti­cella non è un oggetto puntiforme, come
facciamo a dire dove si trova e con quale velocità si muove, dato che un’onda non sta in un posto preciso ?
Secondo il principio di indeterminazione di Hei­senberg è impossibile determinare contempora­neamente sia la posizione sia la quantità di moto di un corpo.
Analogamente è impossibile determinare contem­poraneamente sia la velocità sia l’energia di un corpo.
Ma tra queste coppie di grandezze esiste una di­suguaglianza:
Δx Δp > h

ΔE Δt  > h

Nel 1928 Dirac giunse a una sintesi della mecca­nica quantistica e della relatività, grazie alla quale si previde l'esistenza del positrone e più in gene­rale dell’antimateria.

Erwin Schrodinger e l'onda di probabilità.
Nel 1925 Schrodinger elabora una teoria in grado di spiegare il comportamento degli atomi con molti elettroni.
Si tratta di un'equazione basata sulla teoria onda – corpuscolo della materia di De Broglie e la cui soluzione è detta funzione d'onda.
La funzione d'onda esprime la probabilità di tro­vare un elettrone in una data posizione dello spa­zio atomico; all'elettrone è associata un'onda che corrisponde ad una nuvola di probabilità che cir­conda il nucleo.
Questa nuvola fu chiamata orbitale; entro gli orbi­tali c'è una probabilità del 90% di trovare l'elet­trone.
La probabilità del gatto di  Schrodinger
In una stanza perfettamente isolata dall'esterno, un perfido fisico chiude

1. un atomo radioattivo,
2. una fiala di un potente veleno
3. un gatto.

L'atomo è in uno stato tale per cui, a una certa ora, avrà uguale probabilità di essere o no deca­duto. Il fisico ha anche collegato l'atomo al vele­no in modo che questo sia liberato se l'atomo de­cade. Il veleno è abbastanza potente da uccidere immediatamente il gatto.
All'ora convenuta il fisico aprirà la stanza. Cosa troverà? Un attimo prima dell'apertura, lo stato che descrive il sistema totale della stanza (atomo più fiala più gatto) sarà

• con probabilità del 50% per cento nella configurazione in cui l'atomo non è deca­duto, la fiala di veleno è intatta e il gatto è illeso.
• Con probabilità del 50% il fisico si trove­rà davanti l'atomo decaduto, il veleno li­berato e il gatto morto.

La funzione d’onda di Scrodinger descrive l’onda di materia conoscendo tempo e spazio; essa indica la probabilità di trovare la particella in una data posizione ed in un dato istante per unità di volume. Una particella ha una certa probabilità di trovarsi in una zona in cui non potrebbe mai trovarsi per la fisica classica.

 

Spettro elettromagnetico	frequenza	Lunghezza d’onda
Onde radio	< 3 Ghz	> 10 cm
Microonde	3 GHz – 300 GHz	1mm – 10cm
Infrarossi	300 GHz – 428 THz	700nm – 1 mm
Luce visibile	428 THz – 749 THz	400 nm – 700 nm
Ultravioletti	749 THz – 30 PHz	10 nm – 400 nm
Raggi X	30 PHz – 300 EHz	1 pm – 10 nm
Raggi gamma	> 300 EHz	< 1 pm