I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Equazioni dell’adiabatica reversibile di un gas ideale
Quando un sistema subisce una trasformazione adiabatica, cioè senza scambiare calore con l’esterno, l’equazione del primo principio della Termodinamica (dE=dQ-dL per una trasformazione infinitesima) diventa dE=-dL , poiché dQ=0.
Dalla definizione di calore molare a volume costante, cv = ![]() , troviamo dE = cv dT.
, troviamo dE = cv dT.
Poiché il gas non compie né subisce lavoro diverso dal lavoro di volume nelle sue trasformazioni dovute a variazioni di temperatura e pressione, e trascurando il lavoro dovuto alle forze interne (nulle nel caso dei gas ideali), abbiamo che dL=P'dV, dove P' è la pressione esterna Pe nel caso di espansione, e la pressione P del gas nel caso di compressione. Nel limite reversibile abbiamo in ogni caso .dL=PdV. Pertanto nelle trasformazioni adiabatiche dei gas ideali nel limite reversibile viene rispettata l’equazione differenziale
cv dT = -PdV (1)
Volendo esprimere questa equazione in termini di volume e temperatura, sostituiamo nella (1) P con RT/V, e otteniamo:
cv dT = -![]() dV
dV
Separando le variabili abbiamo pertanto:
![]() = -
= - ![]()
![]()
che, integrata, diventa lnT = - ![]() lnV + costante, e quindi lnT +
lnV + costante, e quindi lnT + ![]() lnV = costante.
lnV = costante.
Quest’ultima equazione può essere riscritta come
![]() = costante
= costante
quindi ![]() = ecostante.
= ecostante.
Poiché ecostante è anch’esso una costante, possiamo scrivere
![]() = costante (2)
= costante (2)
Ricordando che R= cp-cv, e quindi R/cv = (cp-cv)/cv = g -1, con g = cp/cv ,
abbiamo dalla (2):
TV g -1 = costante (3)
Volendo esprimere l’equazione dell’adiabatica di un gas ideale in termini di P e V, sostituendo nella (3) T = PV/R abbiamo PVg-1+1/R = costante, cioè PVg = R costante, e quindi
PVg = costante (4)
scrivibile anche nella forma equivalente
P = costante/Vg (4')
La (4) ci dice che P decresce al crescere di V.
Isoterme e Adiabatiche
Per una mole di gas ideale PV=RT, e quindi
P = RT/V (isoterma di un gas ideale) (5)
La (5) rappresenta un ramo di iperbole, e si vede che P e V sono ognuna funzione decrescente dell'altra. La curva che la rappresenta è asintotica su entrambi gli assi V e P, con P che tende a zero quando V tende all'infinito e V che tende a zero quando P tende all'infinito.

Nella figura vengono illustrate due isoterme, alle temperature T1 e T2, con T1 maggiore di T2.
Da queste curve si nota il suddetto andamento asintotico, e si nota che per un dato valore del volume la pressione è tanto più alta quanto maggiore è la temperatura, mentre per un dato valore della pressione il volume è tanto più grande quanto maggiore è la temperatura.
Dalla (4') notiamo che anche le adiabatiche hanno andamento asintotico, con P o V che tendono a zero quando l'altra grandezza (V o P) tende all'infinito. Però le adiabatiche hanno una pendenza (negativa) più pronunziata delle isoterme, con P che decresce al crescere di V più rapidamente di come decresce V al crescere di P. Ciò si può comprendere confrontando la (4') con la (5). Infatti, il denominatore della (4'),Vg , è maggiore del denominatore della (5), V, poichè g = cp/cv è maggiore di uno.
Ciclo di Carnot
Le macchine termiche cicliche sono sistemi che trasformano in lavoro parte del calore di un fluido caldo, e restituiscono detto fluido ad una temperatura inferiore. Il fluido viene nuovamente riportato alla temperatura iniziale, mediante somministrazione di calore o di lavoro, e ri-immesso nella macchina, e quindi subisce una serie di trasformazioni cicliche.
Il ciclo di Carnot è un ciclo termico ideale, compiuto in modo reversibile in una successione di trasformazioni isotermiche ed adiabatiche.
Esso viene illustrato nella figura seguente.
Nel tratto A-B il fluido è in contatto perfetto con un serbatoio termico a temmperatura T1, ed è quindi anch’esso a questa temperatura. Esso si espande in modo isotermo, e compie un lavoro LA,B pari al calore Q1 che esso assorbe dal serbatoio. La sua energia interna resta invariata in questa espansione isoterma. Si suppone che detta espansione avvenga in modo reversibile.
Al punto B il sistema viene termicamente isolato, e continua ad espandersi in modo adiabatico nel tratto B-C, sempre in modo reversibile. In questo tratto il fluido compie il lavoro LB,C a spese della propria energia interna, e quindi si raffredda dalla temperatura T1 alla temperatura T2. Esso viene quindi messo in contatto termico perfetto con un serbatoio alla temperatura T2, e viene compresso lungo il tratto C-D, in modo isotermo e reversibile. In questo tratto, isotermo, non si ha variazione di energia interna, ed il fluido subisce un lavoro di compressione LC,D a spese dell’inerzia del moto della macchina termica. Il fluido non assorbe l’energia di questo lavoro subito, ma la cede interamente al serbatoio termico sotto forma di calore Q2, in modo da mantenere costante la propria temperatura T2. Il fluido viene nuovamente isolato termicamente, e la sua compressione continua in modo adiabatico, sempre reversibilmente, nel tratto D-A. In quest’ultimo tratto il fluido incamera l’energia dovuta al lavoro LD,A subito, il che lo riporta alla temperatura iniziale T1.

Ciclo di Carnot
Il rendimento R di una macchina termica è definito come il rapporto tra il lavoro compiuto, o meglio utilizzato, e l’energia assorbita.
Nel caso illustrato, il fluido compie il lavoro LA,B+LB,C, ma questo lavoro non è tutto utilizzato, perché la macchina in moto deve restituire al fluido un’energia pari al lavoro LC,D+LD,A, che deve compiere su di esso per riportarlo allo stato iniziale. Il lavoro utile è quindi LA,B+LB,C - LC,D-LD,A, dove La trasformazione inizia in A e termina in A, ed è quindi ciclica. Essa non può comportare perciò variazioni dei valori di funzioni di stato. L’energia interna varia solo nelle adiabatiche B-C e D-A, per cui DEB,C e DED,A sono eguali in modulo e di segno opposto. Lo stesso vale per LB,C e LD,A, ed il lavoro utile è perciò LA,B-LC,D. L’energia assorbita è pari alla quantità di calore Q1, e quindi il rendimento è:
R = (LA,B-LC,D) / Q1 (6)
Ma abbiamo visto che LA,B = Q1 e LC,D = Q2, per cui
R = (Q1 - Q2) / Q1 (7)
oppure R = 1- Q2 / Q1 (8)
Notiamo che il lavoro compiuto dal fluido, reversibilmente, è dato dall’integrale del differenziale PdV dal punto A al punto C, ed è rappresentato nella figura dall’area sotto la curva ABC. Parimenti, il lavoro subito dal fluido è rappresentato dall’area sotto la curva CDA. Il lavoro utile è la differenza tra queste due aree, e corrisponde perciò all’area racchiusa nel ciclo.
Il rendimento di un ciclo di Carnot dipende solo dai valori delle due temperature T1 e T2. Per dimostrare ciò ricordiamo che questo ciclo ideale viene compiuto in mosdo reversibile, perciò i calori veri scambiati sono eguali ai calori scambiati reversibilmente, e quindi in ogni tratto dQ=TdS. Da ciò vediamo che nelle adiabatiche non vi è variazione di entropia, perché non vi è scambio di calore. Le variazioni di entropia nelle due isoterme sono DS1=Q1/T1 e DS2= -Q2/T2 , ma la trasformazione ciclica non può comportare variazioni di entropia, per cui DS1+DS2=0 e quindi Q1/T1 = Q2/T2 . Perciò Q2 /Q1 = T2 /T1, e la (8) può essere scritta nella forma
R = 1- T2 / T1 (9)
oppure R = (T1 - T2) / T1 (10)
Perciò il rendimento cresce al crescere del divario tra le temperature dei due serbatoi, ed un ciclo di Carnot utilizzerebbe tutta l’energia Q1 assorbita se il serbatoio freddo fosse allo zero assoluto.
Abbiamo visto che i lavori relativi alle due adiabatiche si compensano, e solo le isoterme contribuiscono al bilancio di energia. Le adiabatiche sono però utili in quanto consentono di allontanare tra di loro le due isoterme, come appare chiaramente dalla figura, facendo così aumentare il divario tra le due temperature ed il rendimento del ciclo.
Diagrammi S,T
Riportando sugli assi cartesiani l’entropia e la temperatura assoluta, un ciclo di Carnot assume una forma rettangolare. Infatti, le isoterme sono hanno andamento rettilineo orizzontale mentre le adiabatiche reversibili hanno andamento rettilineo verticale, poiché dS = dQ/T =0.
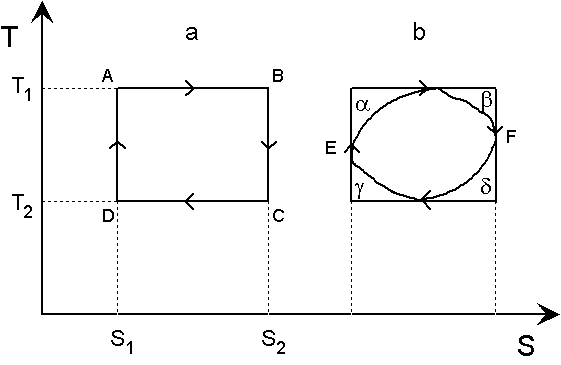
Nel piano S,T l’area sotto una linea corrispondente ad una trasformazione reversibile rappresentano la quantità di calore scambiata in tale trasformazione, poiché dQ=TdS.
Nel ciclo di Carnot, rappresentato nella figura a, il calore Q1 assorbito dal fluido dal serbatoio a temperatura T1 ed il calore Q2 ceduto al serbatoio a temperatura T2 sono dati rispettivamente dalle aree rettangolari sotto i segmenti AB e DC, e quindi Q1= T1DS e Q2= T2DS, con DS = S2 - S1.
Pertanto il rendimento è:
R = (Q1- Q2)/Q1 = (T1DS - T2DS)/ T1DS = (T1- T2)/T1 = 1-T2/T1 = 1- Q2/Q1. Ritroviamo così le equaziono (7-10).
Possiamo dimostrare che nessun ciclo operante tra due temperature estreme T1 e T2 puo’ avere un rendimento superiore a quello del ciclo di Carnot tra dette temperature. Ciò può essere compreso osservando la figura b. Ogni ciclo operante tra una temperatura massima T1 ed una temperatura minima T2 può essere inscritto in un ciclo di Carnot operante tra queste due temperature.
Ricordiamo che le quantità di calore nelle trasformazioni reversibili sono rappresentate dalle aree sotto le linee che rappresentano le trasformazioni, e quindi il calore assorbito dal ciclo generico, che supponiamo effettuato in modo reversibile, è misurato dall’area sotto la curva EF e vale Q1-a-b, mentre il calore restituito da questo ciclo, misurato dall’area sotto la curva di ritorno FE, è dato da Q2+g+d. Se scriviamo il rendimento di questo ciclo di Carnot nella forma R=1-Q2/Q1, troviamo per l’altro ciclo R=1-( Q2+g+d)/( Q1-a-b), e quindi un rendimento inferiore. Se poi detto ciclo venisse effettuato in modo non reversibile, il suo rendimento sarebbe ancora più basso.
Fonte: https://www.docenti.unina.it/downloadPub.do?tipoFile=md&id=30955
Sito web da visitare: https://www.docenti.unina.it
Autore del testo: indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve