I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Supponiamo di essere al centro di una stanza e di volerci spostare in linea retta di 1 m. Possiamo sapere qual è il punto finale che raggiungeremo? La risposta è negativa dal momento che non sappiamo in che direzione e in che verso dobbiamo spostarci. Possiamo trovarci in uno qualunque dei punti di una circonferenza di raggio pari a 1 m. È importante dare, oltre all'intensità dello spostamento, anche la sua direzione (la retta lungo la quale ci si sposta, es.: orizzontale, verticale) e il suo verso (ad esempio: da destra a sinistra o viceversa).
Le grandezze fisiche caratterizzate da un'intensità, da una direzione e da un verso prendono il nome di grandezze vettoriali o vettori. I vettori si indicano con una freccia sopra la lettera che rappresenta la grandezza fisica associata a quel vettore. Ad esempio il vettore spostamento si indicherà con 
. L'intensità del vettore spostamento invece verrà indicata con la lettera, priva della freccia, ossia con s. Nel nostro caso l'intensità del vettore spostamento è di un metro e possiamo pertanto scrivere s = 1 m. Come vedremo, in molte applicazioni è importante chiarire il punto d'applicazione del vettore, ossia il punto in cui è disegnata la coda del vettore.
Andiamo ora a introdurre le regole con cui si possono sommare due vettori. Partendo sempre dal nostro esempio degli spostamenti, prendiamo due spostamenti consecutivi e costruiamone graficamente la somma, come nella figura seguente:
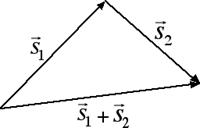
Come emerge dal disegno riportato sopra il vettore somma è un vettore che ha per punto iniziale il punto iniziale del primo vettore e per punto finale il punto finale del secondo vettore. È importante sottolineare come il vettore somma abbia in generale una intensità minore rispetto alla somma delle intensità dei singoli vettori. In un triangolo infatti la lunghezza di un lato è sempre minore della somma degli altri due. C'è però il caso particolare in cui le direzioni dei due vettori sono coincidenti, ossia i due vettori giacciono sulla stessa retta. In questo caso, se i versi dei due vettori sono concordi, il vettore somma ha per intensità la somma delle intensità, se invece i versi sono discordi allora il vettore somma ha per intensità la differenza delle intensità, come emerge dalla figura seguente:
Notiamo come nei casi che abbiamo visto in questa sezione la coda del secondo vettore coincide con la punta del primo vettore. In questi casi si parla di metodo punta-coda per sommare due vettori. Nella prossima sezione vedremo che esiste anche un'altra regola di fondamentale importanza per sommare due vettori.
Un'altra regola con cui si sommano i vettori in fisica quando hanno lo stesso punto di applicazione (ossia la stessa coda) è la cosiddetta regola del parallelogramma. Supponiamo che un uomo si sposti in maniera obliqua su una barca, che a sua volta si sposta orizzontalmente rispetto alla riva di un fiume. Qual è lo spostamento totale dell'uomo rispetto alla riva? È chiaro che entrambi i vettori spostamento vanno applicati allo stesso punto (l'uomo che si sta muovendo):
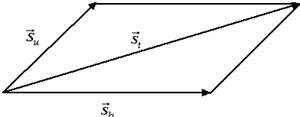
Lo spostamento totale dell'uomo rispetto alla riva è dato dalla diagonale del parallelogramma che ha per lati lo spostamento dell'uomo (u) rispetto alla barca e lo spostamento della barca (b) rispetto alla riva. Per la particolare costruzione geometrica adottata questa regola per sommare due vettori va anche sotto il nome di regola del parallelogramma.
Prima di procedere, notiamo come l'uomo sia stato modellizzato con un punto materiale. Questa è una idealizzazione che useremo spesso: un corpo esteso dotato di massa verrà visto come un punto materiale nel quale possiamo pensare concentrata tutta la massa del corpo. Questo punto prende anche il nome di baricentro del corpo. Se il corpo ha forma regolare il baricentro coincide con il suo centro di simmetria: ad esempio, il baricentro di una sfera omogenea coincide con il centro della sfera.
Perché, quando camminiamo sotto la pioggia, dobbiamo tenere l'ombrello inclinato in avanti per non bagnarci? La risposta sta proprio nel modo in cui si sommano i vettori. Infatti, le gocce di pioggia (p) si spostano verticalmente rispetto al suolo a causa della loro forza-peso. Se l'uomo si sposta rispetto al suolo orizzontalmente da destra a sinistra, è come se il suolo (s) si muovesse rispetto all'uomo orizzontalmente da sinistra a destra. Sommando i due vettori abbiamo che la pioggia rispetto al viandante cade in maniera obliqua e l'ombrello va inclinato in avanti.
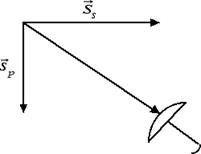
Per concludere questa sezione ricordiamo qual è la regola per moltiplicare un numero per un vettore. Supponiamo di moltiplicare un vettore di intensità s per un numero k positivo. Otterremo un vettore che ha stessa direzione e stesso verso e per intensità k · s. Se invece moltiplichiamo il vettore per un numero k negativo avremo un vettore con la stessa direzione, intensità k · s e verso opposto. In particolare due vettori si dicono opposti quando hanno stessa direzione, stessa intensità ma verso opposto. I vettori opposti sono importanti per il calcolo della differenza di due vettori: infatti la differenza di due vettori si definisce come la somma del primo vettore e dell'opposto del secondo vettore.
Un'altra operazione importante per quelle che sono le applicazioni alla fisica è la scomposizione di vettori rispetto a due assi. Noi ci limiteremo in questa sezione alla scomposizione di un vettore rispetto a due assi perpendicolari tra loro, ad esempio i due assi cartesiani x e y. La scomposizione di un vettore è un po' l'operazione inversa rispetto alla somma: assegnato un vettore, si tratta di trovare due vettori, uno di direzione orizzontale e l'altro verticale, la cui somma riproduca il vettore di partenza. La procedura che dobbiamo seguire è quella della proiezione geometrica del vettore lungo gli assi: partendo dalla punta del vettore dobbiamo tracciare una linea orizzontale e una linea verticale come nella figura sottostante. Queste due linee intersecano gli assi cartesiani in due punti, che diventano le punte dei due vettori richiesti:
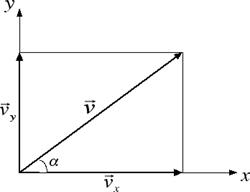
Applicando il teorema di Pitagora abbiamo che le intensità dei tre vettori v, vx e vy sono legate tra loro dalla relazione v2 = v2x + v2y.
Prima di passare agli esercizi, vogliamo ricordare come moltissime grandezze fisiche in natura sono grandezze vettoriali: oltre allo spostamento, sono dei vettori la velocità e l'accelerazione che incontreremo a più riprese durante queste lezioni. Le forze sono caratterizzate da una direzione (la retta d'azione della forza), da un verso, da un punto d'applicazione e dall'intensità misurata dal dinamometro. Pertanto anche le forze sono dei vettori. Esistono tuttavia anche delle grandezze fisiche caratterizzate solamente da un'intensità: tali grandezze sono dette grandezze scalari. Tipici esempi sono la massa di un corpo o la sua temperatura.
Risposta: Con i dati a disposizione non si può dare una risposta univoca. Infatti sappiamo che i vettori, oltre che dalla direzione e dall'intensità, sono caratterizzati da un verso e il testo dell'esercizio non ci dice nulla sul verso dei due vettori. Le risposte possibili sono due: se i due vettori hanno lo stesso verso allora l'intensità dello spostamento totale sarà la somma delle singole intensità sT = 35 m. Se invece i due vettori hanno verso opposto allora lo spostamento totale sarà un vettore che ha la stessa direzione dei due vettori spostamento, il verso coincidente con quello di intensità maggiore e per intensità la differenza delle due intensità:
sT = (20 - 15) m = 5 m.
Risposta: L'angolo formato dalle due forze è pari a 90°. Pertanto, applicando la regola del parallelogramma, avremo che la forza totale è data dalla diagonale di un rettangolo che ha per lati le due forze. L'intensità della forza totale sarà la lunghezza di tale diagonale. Per calcolarla possiamo usare il teorema di Pitagora oppure ricordarci che 3, 4 e 5 costituiscono una terna pitagorica al pari di tutti i loro multipli. Se moltiplichiamo per 5 ogni elemento della terna otteniamo che 15, 20 e 25 costituiscono un'altra terna pitagorica. Pertanto la forza totale avrà un'intensità di 25 N.
Risposta: La scomposizione di un vettore lungo due assi ortogonali si può eseguire agevolmente per un angolo α generico solo se si conoscono le regole della trigonometria. In caso contrario possiamo comunque scomporre un vettore in alcuni casi particolari, come quelli di questo esercizio, dove possiamo applicare le regole della geometria piana.
Se α = 45° le due componenti Fx e Fy sono uguali e pertanto diventano i lati di un quadrato di cui 10 N è la lunghezza della diagonale. Ora, in ogni quadrato la diagonale d = 1.41 · l, ossia la diagonale si ottiene moltiplicando il lato per 1.41. Di conseguenza se conosciamo la diagonale d = 10 N, possiamo ricavarci il lato, che è uguale alle due componenti cercate, dividendo la diagonale per 1.41: l = Fx = Fy = 10 N / 1.41 = 7.09 N.
Se invece α = 60° la figura che si viene a creare è uguale alla metà di un triangolo equilatero di lato F = 10 N. A questo punto Fx ed Fy sono rispettivamente la metà del lato e l'altezza del triangolo equilatero. Pertanto avremo che Fx = 10 N / 2 = 5 N e Fy = 0.866 · 10 N = 8.66 N.
Fonte: http://digilander.libero.it/quantum2008/APPUNTI/Nuova_cartella/Vettori.doc
Sito web da visitare: http://digilander.libero.it/quantum2008
Autore del testo: non indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve