Ingegneria forza elastica

La forza elastica

Si consideri una molla nel suo stato di riposo, cioè quando non è compressa né tirata; uno dei due capi è fisso, mentre all’altro capo, che è libero, è attaccato un oggetto assimilabile ad una particella. Se esercitiamo una certa azione sulla molla tirando il blocco verso destra, la molla eserciterà una azione di richiamo verso sinistra tendendo a ripristinare il suo stato di riposo. Se, al contrario, esercitiamo una azione verso sinistra comprimendo la molla, la molla a sua volta eserciterà una azione elastica tentando nuovamente di ripristinare il suo stato di riposo. Per molte molle si può ritenere che la forza F esercitata dalla molla sia proporzionale allo spostamento d del capo libero della molla rispetto allo stato di riposo. Tale forza è descritta dalla legge di Hooke
La legge di Hooke mette in relazione la forza applicata e lo spostamento (inteso come allungamento o accorciamento) di una molla.
La forza F di richiamo esercitata da una molla è proporzionale, secondo un coefficiente di elasticità k, allo spostamento d dalla sua condizione di riposo ed ha verso contrario ad esso:

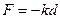
Lo spostamento è in genere un allungamento, ma può anche essere un accorciamento se la molla in condizione di riposo non ha le spire a contatto. Appendendo una molla ad un gancio e attaccando alla molla un peso, la molla si allunga per effetto della forza esercitata dal peso e l'allungamento si arresta quando la forza peso viene equilibrata dalla forza elastica.

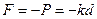
Se si aumenta il peso applicato alla molla, l'allungamento della molla cresce in modo direttamente proporzionale, fino ad un limite di elasticità. Se si supera tale limite, le deformazioni della molla divengono anelastiche, cioè permanenti; scaricando tutto il peso dalla molla, essa si trova ad avere una lunghezza maggiore che all'inizio.
k è la costante di Hooke e si misura in N/m; più k è grande e più la molla è rigida, ovvero occorre una forza maggiore per produrre un dato allungamento.
Se una massa m viene vincolata ad una molla posta su un piano orizzontale e la molla viene allungata e poi lasciata libera, la massa compirà delle oscillazioni armoniche intorno alla posizione di riposo con un periodo pari a
#

In effetti, la legge fondamentale della dinamica ci permette di calcolare l’accelerazione di un corpo di massa m soggetto alla forza elastica:

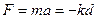
da cui

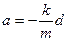
Come si vede l’accelerazione è direttamente proporzionale allo spostamento del corpo ed è sempre rivolta nel senso opposto ad esso.
Ricordando che l’accelerazione vale

e che

si ha che

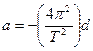
Dall’uguaglianza

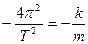
si ricava la relazione # espressa in precedenza.

Esercizio svolto

Ad una molla, fissata ad un sostegno, si appende un oggetto che pesa 1,26N e si ottiene un allungamento di 9cm.

• Quanto vale la costante elastica della molla?

Appendendo alla molla un oggetto di peso diverso si ottiene un allungamento di 13cm

• Quanto pesa l’oggetto?

Soluzione

La molla segue la legge di Hooke

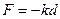
Poiché la forza peso è uguale alla forza elastica si ha:

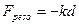
Da cui si ricava la costante elastica k

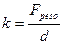
dove d indica l’allungamento. Introducendo i dati, tenendo conto di portare le misure nel SI, si ha

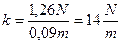
Nel secondo caso, applicando la legge di Hooke, in cui si sostituisce la forza peso al posto della forza elastica  si ha:

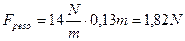
Esercizi proposti

ESERCIZIO N°1

Una molla, appesa a un sostegno e caricata con un peso di o,96N, si allunga di 12cm.

• Quanto vale la costante elastica?

Appendendo alla molla un peso diverso essa si allunga di 18cm

• Quanto vale il peso?

ESERCIZIO N°2

Una molla è lunga 12cm e ha la costante elastica di 7,5N/m. Appendendo alla molla un peso di 0,45N quale lunghezza raggiunge la molla?

ESERCIZIO N°3

La costante elastica di una molla è 10N/m. Appendendo alla molla un peso essa si allunga di 5cm.

• Quanto vale il peso?
• Di quanto si allunga la molla appendendo un peso di 1N?

Esercizio svolto

Un punto materiale di massa m = 300 g è sospeso ad un filo. La massa è sottoposta alla forza di una molla ideale, priva di peso, la cui costante elastica è k = 10 N/m e di cui l’altro estremo è fissato ad una parete verticale. Sapendo che per 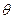= 30° il sistema è in equilibrio con la molla orizzontale, determinare l’estensione x della molla rispetto alla sua lunghezza a riposo
.

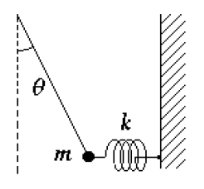
Soluzione

Le forze applicate alla massa M sono il peso, la forza elastica e la tensione T della fune. Scegliamo
un sistema di riferimento con l'asse x orizzontale diretto a destra e l'asse y diretto verso l'alto.
Allora, all'equilibrio, detta x l'estensione della molla:

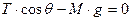
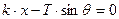
queste relazioni si possono scrivere:

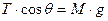
dividendo la seconda per la prima si ricava:

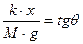
da cui ricavo x:

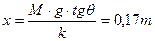
Seconda legge di Newton applicata al moto circolare

Consideriamo ora una situazione molto comune associata ad una particella che si muove con moto circolare uniforme. Si è visto che una particella che si muove con velocità costante in modulo su una circonferenza di raggio r ha un’accelerazione di modulo

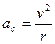
Il vettore accelerazione con questo modulo è diretto verso il centro della circonferenza ed è sempre perpendicolare a v.
In accordo con la legge di Newton, se c’è un’accelerazione vi deve essere una forza netta diretta verso il centro della circonferenza perché l’accelerazione ha quella direzione. Indipendentemente dalla natura della forza agente sulla particella in moto circolare, possiamo applicare la seconda legge di Newton alla particella lungo la direzione radiale:

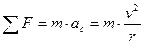
In generale, un oggetto si può muovere lungo una traiettoria circolare sotto l’azione di vari tipi di forze o una composizione di forze. Se la forza agente sull’oggetto divenisse nulla, l’oggetto non si muoverebbe più sulla traiettoria circolare ma si muoverebbe lungo una linea retta tangente alla circonferenza.

Se, ad esempio facciamo ruotare una pallina legata a un filo, essa descriverebbe una circonferenza finché è in moto ma non appena il filo si spezza la palla continua a muoversi lungo una linea retta tangente alla circonferenza nel punto dove il filo si è spezzato.

Rifletti

Stai girando su una ruota panoramica con velocità costante. La cabina nella quale siedi si mantiene sempre nella corretta orientazione verticale. Qual è la direzione della tua accelerazione centripeta quando stai nella sommità della ruota? Nel punto più basso della ruota? Qual è la direzione della forza normale che il sedile applica su di te quando ti trovi nel punto più alto della ruota? E nel punto più basso della ruota?

Curva pericolosa
Un'auto di 1000 kg impegna una curva di raggio 80 m a 100 km/h. La forza centripeta necessaria per curvare è fornita dalla forza di attrito statico tra gomme e strada. Riuscirà l'auto a chiudere la curva senza uscire di strada se il coefficiente d'attrito vale 0,8?

La forza centripeta necessaria per mantenere la curva vale

La massima forza d'attrito statico è proporzionale alla forza normale, cioè al peso della macchina


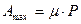
Risposta al problema.
La forza d'attrito non riesce a fornire la forza centripeta necessaria alla curva, ne consegue che l'auto curva ma non abbastanza, con un raggio di curvatura maggiore di R e quindi esce di strada.
Cosa dovrebbe fare l'autista per evitare l'incidente?
La forza centripeta dipende dalla massa, dalla velocità e dal raggio di curvatura. L'autista può agire solo sulla velocità dell'automobile e diminuirla fino ad ottenere una forza centripeta almeno uguale al massimo attrito disponibile.

Quindi


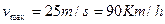
Seconda risposta al problema.
Decelerando fino a 90 km/h la forza necessaria per curvare uguaglia la forza di aderenza tra gomme e strada. Per una maggiore sicurezza l'autista dovrebbe tenersi a velocità inferiore a 90 km/h.

Fisica e realtà

Una macchina viaggia su una strada circolare di raggio r. La strada è piana e la macchina viaggia ad alta velocità in modo tale che la forza di attrito che causa l’accelerazione centripeta è al suo massimo valore possibile. Se la stessa macchina è condotta su un altro percorso circolare di raggio 2r e il coefficiente di attrito fra i pneumatici e la strada è lo stesso di quello della strada precedente, qual è la massima velocità che la macchina può sostenere senza slittare sulla strada?

Esercizio svolto
Al luna park

Nel rotore del Luna Park una persona viene fatta ruotare molto velocemente dentro un cilindro. La persona rimane bloccata contro la parete quando il pavimento del cilindro viene aperto. Il coefficiente di attrito statico tra la persona e la parete è 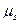ed il raggio del cilindro è R.
a) determinare il massimo periodo di rotazione necessario perché la persona non cada.
b) dare un valore numerico per T se R=4.00m e 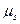=0.400.Quanti giri al minuto deve compiere il cilindro?

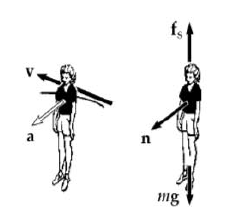
Soluzione

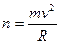
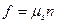
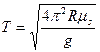
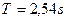
Ancora sull’auto in curva

Un’automobile di massa m=1600 kg viaggia con velocità costante su una pista circolare di raggio R = 190 m.  Quale è il valore minimo del coefficiente di attrito 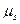 (pneumatici-terreno) che impedisce alla macchina di slittare verso l’esterno ?

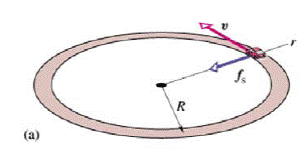
Idee chiave

• se l’auto percorre una  traiettoria circolare è sottoposta a forza centripeta
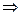• l’ unica forza orizzontale che agisce sull’ auto è l’attrito    forza centripeta = attrito
• l’auto non slitta verso l’esterno quindi si tratta di un attrito statico
• se l’auto è sul punto di slittare il modulo della forza di attrito è massimo

Sapendo che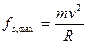                                    
e che                                                   
si ha:

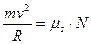
da cui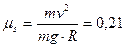                                                  
Pertanto se 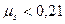 l’auto slitta verso l’esterno

La macchina in una curva sopraelevata

Un ingegnere vuole progettare una rampa sopraelevata per la strada, tale che le macchine non debbano fare  affidamento sull’attrito per affrontare la curva senza  slittare. Si supponga che l’auto percorra la curva a 48 km/h e che il raggio della curva sia 50.0 m. Con quale angolazione deve essere sopraelevata  la curva ?

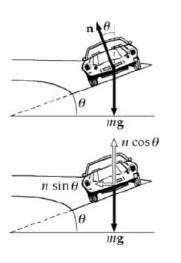
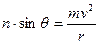
Poiché la somma delle forze lungo y è pari a zero, si ha

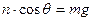
Dividendo membro a membro si ottiene:

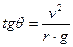
Da cui 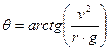= 20,1°

Esercizi proposti

Esercizio n°1

Un’auto di 1500Kg che si muove su una strada orizzontale piana, affronta una curva di 35,0m di raggio. Se il coefficiente di attrito statico tra pneumatici e terreno asciutto è 0,500, trovare la velocità massima che l’auto può mantenere per affrontare con successo la curva
[13,1m/s]

Esercizio n°2

In un giorno piovoso l’auto descritta nell’esercizio precedente comincia a sbandare nella curva quando la sua velocità raggiunge 8,00m/s. In questo caso, qual è il coefficiente di attrito statico?
[0,187]
Esercizio n°3

Un oggetto di massa 0,500Kg è attaccato all’estremità di una fune di lunghezza 1,50m. L’oggetto ruota su una circonferenza orizzontale. Se la fune può sopportare una tensione massima di 50,0N, qual è la massima velocità dell’oggetto prima che la fune si spezzi?
[12,2m/s]
Esercizio n°4

Calcolare la tensione della fune se la velocità dell’oggetto è 5,00m/s
[8,33N]

Esercizio n°5

La curva sopraelevata di un'autostrada è stata progettata per una velocità 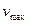. Il raggio della curva è r. In una brutta giornata il traffico percorre l'autostrada alla velocità v.

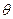• Quanto vale l’angolo di sopraelevazione?
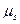• Quanto deve essere il minimo coefficiente d'attrito  che consente di superare la curva senza scivolare verso il basso?
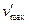• Usando tale coefficiente, con quale velocità massima  è possibile percorrere la curva senza scivolare verso l’alto?

[ = 95 km/h; r = 210 m; v = 52 km/h]

Esercizio n°6

Calcolare la velocità periferica di un corpo di massa m = 0,5 kg che si muove con velocità angolare ω= 0,6 rad/s lungo una circonferenza di raggio r = 1m. Quanto valgono l'accelerazione e la forza centripeta?
Ris.: v = 0,6 m/s, a = 0,36 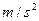, F = 0,18N

Esercizio n°7

Un disco con raggio R = 25 cm ruota con velocità angolare costante intorno ad una retta perpendicolare ad esso e passante per il suo centro. Un punto materiale A appartenente al bordo percorre un arco di 5 cm in 0,1 s. Calcolare:
a) la velocità periferica e la velocità angolare
b) l'accelerazione centripeta
c) il periodo e la frequenza del moto
d) il valore della forza che impedisce al punto di staccarsi, se la sua massa è pari a 2 g
Ris.: a) v = 0,5 m/s, ω= 2 rad/s; b) T = 3:14 s,f = 0,32Hz; c)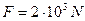

Esercizio n°8

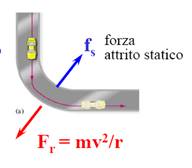
Un'autovettura percorre una curva di raggio R = 50m. Sia il coefficiente di attrito tra pneumatici e asfalto.
A - Si calcoli la velocità massima con cui l'auto può percorrere la curva senza sbandare. 

B - Si supponga che la curva sia sopraelevata, ovvero giaccia su un piano inclinato con inclinazione  di 10° rispetto all'orizzontale, qual è in questo caso la velocità massima con cui l'auto può percorrere la curva senza sbandare?

Esercizio n°9

Lungo la curva sopraelevata disegnata in figura, supposta circolare e di raggio R=200m, in una strada larga 12m (lato BC del triangolo BAC in figura) e realizzata in modo tale da avere coefficiente di attrito trascurabile, il limite di velocità è di 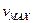=100 km/h. Calcolare di quanto il bordo esterno della strada, lato BA, debba essere rialzato rispetto a quello interno, affinché l’autovettura, procedendo alla massima velocità consentita, non sbandi uscendo fuori strada.

Esercizio n°10

Un ingegnere vuole progettare una rampa sopraelevata  per la strada, tale che le macchine non debbano fare  affidamento sull’attrito per affrontare la curva senza  slittare. Si supponga che l’auto percorra la curva a 48 km/h e che il raggio della curva sia 50.0 m. Con quale angolazione deve essere sopraelevata  la curva ?

Esercizio n°11

Un’automobile di massa m=1000 kg percorre una curva piana di raggio costante r=80 m con una velocità costante di 60 km/h. Determinare il minimo coefficiente di attrito statico tra asfalto e ruote dell’automobile  necessario perché l’automobile si mantenga  la traiettoria curva.

Esercizio n°12

Un’automobile sta percorrendo una curva di raggio 30 metri. Il coefficiente di attrito tra pneumatici e fondo stradale è 0,7.
Qual è la massima velocità con cui l’automobile può percorrere la curva senza pericolo?
Se nevica e il fondo stradale è viscido, il coefficiente di attrito si riduce a 0,2. In queste condizioni qual è la massima velocità che l’automobile può raggiungere senza slittare?
Che cosa accade se l’automobile supera la massima velocità?
[51Km/h; 27,6Km/h]
Esercizio n°13

Una curva ha il fondo stradale inclinato di 30° rispetto al piano orizzontale.
Se l’automobile di massa 900Kg percorre la curva, a quale forza centripeta è soggetta?
Se il raggio della curva è di 150m, a quale velocità massima può viaggiare l’automobile senza slittare?
Se la curva fosse piana quale dovrebbe essere il coefficiente di attrito per mantenere l’automobile sulla strada a parità di velocità?
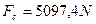[; v=105Km/h; k=0,58]

Esercizio n°14

Alida si diverte a far ruotare a 10 giri/s intorno al dito una catenina con un ciondolino di massa 20g su una circonferenza orizzontale di raggio 12cm. La catena supporta al massimo la tensione di 9N senza spezzarsi.
Qual è la massima velocità che può avere il ciondolino (trascurando il peso)?
Un ciondolino di massa doppia a quale velocità potrebbe ruotare?
(suggerimento: la tensione nella catenina è la forza centripeta)
[7,35m/s; 5,2m/s]

Esercizio n°15

Una pallina di massa 200g ruota su una circonferenza verticale di raggio 30cm, trattenuta da un filo di nylon teso durante la rotazione.
Qual è la minima velocità che deve avere la pallina nel punto più alto della traiettoria perché il filo non si allenti?
Se la pallina passa per il punto più alto con una velocità doppia, qual è la tensione del filo?
[v=1,7m/s; T=15,4N]
Esercizio n°16

Una pallina di 150g, trattenuta da un filo di nylon, viene fatta ruotare su una circonferenza verticale di raggio 40cm. La massima tensione che il filo può sopportare è 2N
Qual è la massima velocità che può avere la pallina nel punto più alto della circonferenza?
E nel punto più basso?