Ingegneria lavoro di una molla

CALCOLO DEL LAVORO DI UNA MOLLA

In questi appunti calcoleremo una grandezza molto importante: otterremo la formula che dà il Lavoro eseguito da una molla mentre si allunga/accorcia.

Se io allungo/comprimo una molla e poi vi collego una pallina, quando lascio andare la molla questa spinge via la pallina, dandole velocità e quindi eseguendo un Lavoro su di essa; tale Lavoro è tanto maggiore quanto più la molla era stata allungata/compressa. Ne segue che il Lavoro fatto dalla molla su di un oggetto esterno (la pallina in questo caso) è tanto più grande quanto più la molla si allunga/accorcia.

Inoltre: se uso due molle, una più rigida e l’altra meno rigida (costante della molla “K” maggiore e minore), noto che a parità di allungamento il Lavoro fatto dalla molla è tanto maggiore quanto più K è grande.

In conclusione: una molla riceve/fornisce Lavoro deformandosi; tale Lavoro aumenta tanto più la molla si deforma o, a parità di allungamento/accorciamento (cioè, a parità di DS), tanto più il valore di K è alto.

Ma qual è la relazione esatta che lega il Lavoro eseguito da una molla con K e DS? Sfruttiamo ciò che abbiamo imparato in altri appunti e calcoliamo l’esatta relazione matematica.

Lavoro di una molla – calcolo grafico
La Forza della molla cambia al cambiare di DS in base alla ben nota formula:
Fm = -Kmolla×DS       (in valore assoluto)                        (1)
Disegniamo il grafico Fm vs. DS (figura 1); per comodità lo disegniamo in valore assoluto, ponendo Fm sempre positivo. Adesso poniamoci questo problema: ho una molla che è stata già deformata di un tratto DSi, io voglio deformarla fino ad un tratto DSf (in pratica: mi danno una molla già deformata inizialmente ed io voglio stirarla/accorciarla un altro po’). Qual è il Lavoro della molla?

Sappiamo che il Lavoro di una forza non costante è uguale all’area sottesa dal grafico forza vs. spostamento, cioè all’area blu di figura 1.

Con un semplice calcolo geometrico arrivo a dire che l’area blu (Ar) è data dalla differenza delle aree dei due triangoli O DSf Hf   e  O DSi Hi  :
Ar = ½                                                                    (2)
Le altezze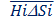
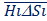  = Kmolla×DSf  
Sostituendo i valori sopra nell’eq. (2) abbiamo che:
Ar = ½DSf×(Kmolla×DSf)  -  ½DSi×(Kmolla×DSi) = ½Kmolla×(DSf2 - DSi2)                                       (3)
Ma poiché l’Area sottesa dal grafico è uguale al Lavoro, otteniamo:
Lavoro fatto da una molla = ½Kmolla×(DSf2 - DSi2)    (con la forza in valore assoluto!)      (4)
Nota che i valori degli spostamenti, DSi e DSf, sono al quadrato, perciò non importa se la molla viene allungata o contratta!

Infine, dobbiamo aggiungere il segno “-“ presente nell’eq. (1) e che noi non abbiamo considerato fino ad ora. Se aggiungo il “-“ alla forza lo devo aggiungere anche al Lavoro e ottengo la formula finale:
Lavoro fatto da una molla = - ½Kmolla×(DSf2 - DSi2) = ½Kmolla×(DSi2 - DSf2)                           (5)
Esempio 1
Supponi di avere una molla con Kmolla=30N/cm. La pongo su di un piano orizzontale, la comprimo di 4cm e ci metto accanto una pallina di massa 200g; dopodiché lascio andare la molla, che spinge via la pallina! Qual è il Lavoro che la molla esegue spingendo via la pallina? Con quale velocità schizza via la pallina?
La molla all’inizio è compressa di 4cm ® DSi=0,04m. Alla fine la molla è libera e perciò ritorna alla sua lunghezza di riposo: DSf=0. La costante della molla è Kmolla=30N/cm; portandola in metri ottengo Kmolla=3.000N/m. Il Lavoro che esegue è perciò (eq. 5): ½×3000×(0,042-02)=2,4J. Nota che ho messo tutto in metri perché l’unità di misura dell’energia è il Joule ed esso si misura in Newton×metro.
Per quanto riguarda la velocità iniziale della pallina, si applica la ben nota equazione: Kf - Ki = Lavoro.
Ki = 0J (la pallina all’inizio è ferma) ; Lavoro = 2,4J (è quello eseguito dalla molla, ottenuto sopra) ® Kf=2,4J. Kf= ½×M×Vf2 ® (sostituendo) ® ½×0,2kg×Vf2  ® Vf = 4,9m/s.

Esempio 2
Un’auto di 1000kg va a sbattere con una velocità di 8m/s contro un respingenti (una grande molla) con Kmolla=1.000N/cm. Di quanto deve contrarsi la molla per fermare l’auto in corsa?
Stessa formula di cui sopra: Kf – Ki = Lavoro. Ki = ½×M×Vi2 = ½×1.000×82 = 32.000J ; Kf=0 (l’auto è stata immobilizzata)  ® Lavoro = -32.000J.
Per quanto riguarda la molla: Kmolla=1.000N/cm = 100.000N/m ; DSi = 0 (all’inizio la molla era a riposo) ; devo trovare DSf.
Lavoro della molla = ½×Kmolla×(DSi2 - DSf2) = ½×100.000×(0 - DSf2) = -32.000J ® DSf = ± 0,8m. Il segno “±” indica che la molla può fermare l’auto o comprimendosi (se l’auto le viene addosso) o stirandosi (se essa viene agganciata dietro l’auto in corsa.
Adesso un secondo problema: quando il respingente è compresso di 0,4m, qual è la velocità dell’auto?
In questo caso DSf = 0,4m ® Lavoro della molla = ½×Kmolla×(DSi2 - DSf2) = ½×100.000×(0 – 0,42) = -8000J. Ki=32.000J , Lavoro della molla = -8000J ® Kf = 24.000J. Un rapido calcolo mostra che Vf = 6,93m/s.