I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
IL Rendimento delle macchine termiche
e il secondo principio della termodinamica
di Ezio Fornero
Contenuti:
Diciamo macchina termica un qualsiasi dispositivo che realizzi una trasformazione di calore in energia meccanica attraverso un processo (o, più esattamente, una serie di processi ciclici) la cui durata sia indefinita. Questo equivale a dire che una macchina termica deve essere in grado di erogare una quantità di lavoro potenzialmente illimitata in un tempo indefinito. Da un punto di vista fisico, non hanno molta importanza la struttura meccanica e i particolari tecnici di una data macchina termica (m.t.); è sufficiente dire che il lavoro di una m.t. è eseguito da un fluido che, assorbendo calore, si espande e produce lavoro: ciò può avvenire in più di un modo, p.es. spostando un pistone o mettendo in rotazione una turbina. Dal punto di vista termodinamico, una m.t. viene identificata nei processi fisici subiti dal fluido motore che la fa funzionare.
È chiaro che i processi termodinamici che avvengono in una m.t. devono essere ciclici, sia perché in generale i motori termici mettono in azione dei rotismi (albero motore, cambio ecc.) sia perché, in ogni caso, un fluido non potrà produrre lavoro espandendosi all’infinito, e quindi si deve pensare che, se il fluido compie lavoro espandendosi, dovrà poi essere ricondotto al volume iniziale. Perciò dobbiamo ammettere che, per poter erogare quantità arbitrariamente grandi di lavoro per tempi indefinitamente lunghi, una macchina termica deve operare secondo una serie di processi termodinamici ciclici.
Per il principio di conservazione dell’energia (meccanica + termica), il lavoro prodotto deve essere ottenuto a partire dal calore; ci dovrà quindi essere una sorgente termica, che fornisca il calore necessario. Dato che il lavoro della m.t. è potenzialmente illimitato, la sorgente termica dovrà essere in grado di fornire quantità di calore arbitrariamente grandi, senza raffreddarsi. Idealmente, ciò significa che la capacità termica di una sorgente di calore deve essere infinita, in modo che, pur continuando a fornire calore, la sua temperatura rimanga costante: perciò, la sorgente ideale deve essere un termostato. In realtà, le macchine “reali” come i motori dei mezzi di trasporto sono alimentate piuttosto da processi di combustione, che trasformano in modo irreversibile la composizione chimica del fluido motore, il quale evidentemente deve essere rinnovato ad ogni ciclo di funzionamento. La “sorgente termica” reale è quindi una trasformazione chimica continuamente rinnovata e non un sistema fisico persistente.
Dal punto di vista economico, l’ideale sarebbe che una m.t. fornisca lavoro convertendo una quantità equivalente di calore dall’ambiente circostante, sfruttando cioè solo l’enorme energia termica contenuta nell’atmosfera, nell’acqua degli oceani, ecc. Un dispositivo del genere non è realizzabile, ma non è vietato dal principio di equivalenza o dalla legge di conservazione dell’energia, che al contrario stabiliscono la possibilità di convertire energia meccanica in energia termica o viceversa, senza alcuna limitazione, secondo il fattore di conversione 1 cal = 4,186 J. Mentre però la trasformazione di energia meccanica in calore ceduto all’ambiente è facilmente realizzabile, è chiaro che il processo inverso è molto più difficile, e non può essere realizzato sfruttando l’ambiente come unica sorgente di calore. Ci deve essere quindi un secondo principio della Termodinamica che limita la possibilità di trasformare il calore assorbito da una sola sorgente in lavoro.
Infatti, tutte le macchine termiche assorbono durante un singolo ciclo di funzionamento una certa quantità di calore Q1 da una sorgente “calda” (cioè, a T maggiore di quella ambiente) e trasformano in lavoro L solo una parte dell’energia termica equivalente a Q1 ; il resto viene disperso, direttamente o indirettamente, sotto forma di calore non utilizzato e irrecuperabile, nell’ambiente esterno, che viene definito “sorgente fredda”. Indichiamo con Q2 il calore ceduto alla sorgente “fredda”, con T1 la temperatura della sorgente “calda”, e con T2 quella della sorgente “fredda”.
In base al principio di conservazione dell’energia, se anche il calore viene espresso in Joule, durante un singolo ciclo di funzionamento il lavoro prodotto sarà dato dall’equazione
L = Q1 - Q2 |
Il calore ceduto Q2 non può mai essere nullo, e quindi il rapporto tra L e Q1 è sempre minore di 1. Tale rapporto si chiama rendimento o “efficienza” di una m.t. ed è adimensionale. Si può esprimere anche in percentuale: 1 = 100%.
Per definizione, si ha quindi
h = |
Il secondo principio nasce dalla scoperta che questa limitazione al rendimento di una qualsiasi macchina termica non deriva da difficoltà tecniche rimediabili e neppure dal fatto che è impossibile isolare termicamente un motore rispetto all’ambiente. Infatti, è vero che se un motore non potesse trasferire calore all’ambiente si surriscalderebbe, e quindi le dispersioni termiche sono praticamente necessarie; ma l’impossibilità di ottenere un rendimento assoluto del 100% deriva da questioni di principio indipendenti da considerazioni pratiche. A questo proposito si introduce il postulato di Kelvin , il quale afferma che è impossibile realizzare una trasformazione il cui unico risultato sia la conversione in lavoro del calore assorbito da una sorgente a temperatura uniforme, cioè è impossibile in linea di principio realizzare una macchina termica ciclica che trasformi integralmente in lavoro il calore fornito da una sola sorgente.
Lo schema degli scambi energetici di una macchina termica – a prescindere dal suo effettivo funzionamento – è il seguente:
SORGENTE CALDA
Q1 = calore assorbito dalla
sorgente calda
Q2 = calore ceduto alla
sorgente fredda
L = lavoro eseguito
L = Q1 - Q2
SORGENTE FREDDA
Esiste una relazione logica di implicazione reciproca tra il Postulato di Kelvin (PK) e quello di Clausius (PC), nel senso che, se uno dei due fosse falso, lo sarebbe anche l’altro. Per esempio, si dimostra che la negazione di PK implica quella di PC, cioè, se fosse possibile costruire una m.t. avente rendimento = 1 , allora sarebbe possibile trasferire del calore da una sorgente fredda a una più calda, senza assorbire lavoro dall’esterno. Perciò, benché apparentemente siano del tutto indipendenti, i due enunciati sono fisicamente equivalenti, ed entrambi possono essere considerati formulazioni particolari del secondo principio (ce ne sono tante, a seconda dell’aspetto che si prende in considerazione).
Neghiamo quindi il Postulato PK ; ciò significa che esiste una m.t. M in grado di convertire integralmente in lavoro L il calore Q1 assorbito da una sola sorgente calda, a temperatura T1.
Perciò, abbiamo l’equazione L = Q1
Possiamo utilizzare questo lavoro per far funzionare un frigorifero “normale”, il quale assorba calore Q2 da una sorgente fredda a temperatura T2 e trasferisca calore alla stessa sorgente calda. Se indichiamo con Q3 la quantità di calore che il frigorifero cede alla sorgente calda, abbiamo, per la legge di conservazione dell’energia:
Q3 = L + Q2
cioè
Q3 = Q1 + Q2
Q3 - Q1 = Q2 .
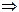 NO PC , e dato che ammettiamo PC come vero, anche PK deve essere vero, per assurdo.
NO PC , e dato che ammettiamo PC come vero, anche PK deve essere vero, per assurdo.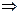 NO PK
NO PK
Una variante è la seguente: la macchina assorbe Q1 e trasferisce Q2 facendo lavoro L = Q1 – Q2 . E’ ancor più paradossale, dato che il calore Q1 – Q2 sarebbe estratto dalla sorgente fredda.
In teoria, una macchina termica può essere reversibile o irreversibile. Un ciclo motore ideale operante tra due sorgenti dovrebbe essere reversibile, dato che l’irreversibilità comporta dispersioni termiche e dissipazione di energia meccanica in calore ceduto all’ambiente (la sorgente “fredda”). Perciò una macchina reale è meno efficiente di una ideale, secondo le disuguaglianze
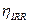 < 1
< 1
valide per macchine operanti tra le stesse sorgenti.
Osservazioni conclusive
In realtà, le considerazioni svolte sul ruolo della sorgente e sul funzionamento di una macchina termica sono molto schematiche. Per cominciare, non è detto che la sorgente “calda” sia effettivamente un termostato, né che essa sia esterna fisicamente alla m.t.; p.es. nei comuni motori a combustione interna (cioè, motori delle automobili e autoveicoli in generale, e anche nelle turbine a gas) la sorgente calda in realtà è sostituita dal processo di combustione di una miscela (benzina o gasolio + aria) interno alla macchina. Il termostato quindi deve essere sostituito nella realtà da un processo indefinitamente ripetibile di produzione di calore, p.es. mediante processi di combustione, che sono anch’essi irreversibili.
Infine, il funzionamento reale di una m.t. implica attriti tra parti meccaniche a contatto, con trasformazione anch’essa irreversibile di energia meccanica in calore.
Possiamo constatare che le macchine reali sono irreversibili anche in base alle seguenti considerazioni. Invertendo un ciclo motore si ottiene un ciclo frigorifero. E’ di fatto impossibile realizzare una macchina refrigerante invertendo tutti i movimenti e gli scambi termici di un motore, proprio perché i motori reali sono irreversibili.
Da un punto di vista termodinamico, le macchine “reali” sono ripetitive piuttosto che cicliche (basti pensare al fatto che nel corso di un “ciclo” di funzionamento si ha una combustione, la quale implica un non-ritorno alle condizioni di partenza).
A prescindere dall’essere il fondamento teorico del funzionamento dei motori termici, la teoria delle macchine termiche ha evidenziato il ruolo dei processi irreversibili in termodinamica. Mentre è possibile che una data quantità di energia meccanica venga integralmente convertita in calore ceduto all’ambiente o in generale a un termostato, non è possibile trasformare integralmente il calore fornito da un termostato in energia meccanica. Questa irreversibilità della conversione di energia meccanica in calore è, come s’è visto, fisicamente equivalente a quella degli scambi termici. Analizzando gli attriti possiamo vedere come la conversione di energia meccanica in calore venga osservata su scala macroscopica, mentre su scala microscopica o molecolare avvengono trasformazioni tra forme di energia ordinata o disordinata. Per esempio, l’energia cinetica di un pistone in moto è “ordinata”, dato che tutte le parti del pistone – al limite, tutti i suoi atomi – si muovono insieme (trascurando moti locali microscopici come vibrazioni atomiche ecc.). Le forze d’attrito trasformano energia ordinata in energia termica, che è la manifestazione macroscopica dell’energia molecolare. Il moto di atomi e molecole è caotico, quindi l’energia termica è disordinata. Gli stati disordinati di un sistema fisico sono generalmente più probabili di quelli ordinati, perciò è più facile realizzare trasformazioni termiche da uno stato iniziale a uno finale meno ordinato che a uno più ordinato, cioè, su scala macroscopica, trasformare lavoro in calore che viceversa. L’irreversibilità può essere interpretata come dovuta al passaggio da stati fisici “più ordinati” e meno probabili a stati “meno ordinati” ovvero “più disordinati” e più probabili.
La temperatura e il caos molecolare di un corpo (escludendo i termostati) che assorbe calore aumentano, perciò una temperatura più alta significa maggior disordine molecolare. Lo zero assoluto [1] sarà la temperatura di un sistema totalmente ordinato; dato che l’energia delle molecole è disordinata, l’ordine perfetto è possibile solo se tutti gli atomi o molecole sono fermi. Perciò, nella Fisica Classica, lo zero assoluto è lo stato di totale immobilità della materia (nella Meccanica Quantistica è solo lo stato di minima energia) – si veda anche la nota a fine testo.
Dunque sembra doversi concludere che i processi “spontanei” generino disordine, cioè un sistema termicamente e meccanicamente isolato evolve verso gli stati più disordinati, in modo che lo stato finale di equilibrio di un sistema isolato non può essere più ordinato di quello iniziale. In breve, il disordine dell’intero Universo aumenta col tempo. Potrebbe sembrare che tale legge non si debba applicare a processi artificiali come quelli prima analizzati, ma in natura non esistono processi “artificiali” , dato che le leggi fisiche sono universali e non distinguono tra processi “naturali” e “artificiali”. Anche i cicli motori operanti nelle macchine reali [2] seguono la legge dell’irreversibile aumento del disordine applicata all’intero universo, che in realtà va inteso come l’unione di un sistema fisico (in questo caso il fluido motore o l’intera macchina) e l’ambiente. Queste considerazioni costituiscono il fondamento concettuale del Secondo Principio della Termodinamica, del quale i postulati di Kelvin e di Clausius sono enunciati particolari.
Tuttavia, la precedente esposizione della seconda legge è assai incompleta, soprattutto per l’imprecisione del concetto di disordine, dal momento che non abbiamo definito come misurarlo.
La misura del disordine è definita da una grandezza fisica detta entropia. L’entropia di un sistema fisico termicamente e meccanicamente isolato non può diminuire, cresce nelle trasformazioni irreversibili e non varia in quelle reversibili. L’aumento dell’entropia separa il passato dal futuro, dato che, per un sistema isolato, l’entropia futura sarà maggiore dell’attuale. Il Secondo Principio afferma che l’entropia dell’Universo deve aumentare col tempo, e le sue formulazioni parziali come i postulati di Kelvin e di Clausius – sebbene limitate apparentemente a fenomeni circoscritti e a problemi tecnici – ne esprimono il significato fisico in via preliminare.
Mentre il primo principio della Termodinamica è una equazione e quindi non indica la direzione in cui un processo fisico avviene e non introduce asimmetrie, al contrario il secondo implica una asimmetria temporale per cui l’Universo non può essere ricondotto in nessuno dei suoi stati precedenti (sebbene esistano trasformazioni cicliche, ma solo su scala locale), vale a dire: la serie degli istanti, in cui pensiamo di dividere il tempo, non può essere invertita. Così sembra che il secondo principio definisca univocamente la direzione del tempo (“freccia del tempo”). Il grande interesse verso il secondo principio, da un punto di vista fisico, trae origine dalla natura fisica dell’irreversibilità. Questo concetto può essere applicato solo a sistemi costituiti da molte particelle a causa del suo carattere statistico, che possiamo riconoscere dalla sua connessione con ordine e disordine – questi termini hanno senso solo se si riferiscono a un grande numero di particelle identiche. La seconda legge traduce in Fisica la legge matematica dei grandi numeri, per cui differisce profondamente dalle altre leggi fisiche della Dinamica e dallo stesso primo principio, e non può essere ricondotta a qualche principio meccanico. [3]
[1] Lo zero assoluto è l’estremo inferiore di ogni scala delle temperature piuttosto che il minimo, dato che nessuna serie di cicli frigoriferi può raggiungere questo punto, mentre in teoria è possibile raggiungere qualsiasi temperatura ad esso superiore. Le scale termiche correntemente usate sono: la scala kelvin (o assoluta), la Celsius e la Fahreneith. La prima e la seconda sono universali, ma secondo il Sistema Internazionale di Unità (S.I.) l’unità fondamentale della temperatura termodinamica è il kelvin (K), non il grado Celsius ( °C ), più usato in pratica. La temperatura termodinamica espressa in K è la “temperature assoluta”, alla quale generalmente si riferiscono i fisici, dato che esprime l’energia cinetica media di atomi e molecole. Ovviamente 0 K corrisponde allo zero asoluto. Il punto triplo dell’acqua è, per convenzione, 273.16 K o 0.01 °C (trascurando alcuni dettagli). La differenza tra due temperature è la stessa nelle due scale, che differiscono per i valori assegnati ai punti fissi. Se “ T ” indica la temperatura in K e “t” in °C, si ha t = T - 273.15 , così lo zero assoluto corrisponde a - 273.15 °C.
La scala Fahrenheit è comunemente usata negli Stati Uniti; la sua unità è il grado Fahrenheit ( °F) . Se “F” indica la temperatura in gradi Fahrenheit, si ha F = 1.8 T - 459.67 , quindi lo zero assoluto è a - 459.67 °F.
[2] Le macchine “reali” operano mediante trasformazioni irreversibili che producono aumento di entropia. Le macchine “ideali” sono reversibili, cioè l’entropia non varia. I due postulati valgono per entrambe, quindi non implicano necessariamente un aumento dell’entropia; questo si verifica comunque perchè le macchine reali sono irreversibili. Viceversa, l’irreversibilità dei motori implica h < 1 .
[3] Le leggi di Newton implicano che tutti i moti sono invertibili rispetto al tempo. La Dinamica classica, la Relatività Ristretta e Generale sono simmetriche rispetto al tempo. Queste teorie implicano che l’Universo evolva a partire da condizioni iniziali lontane da uno stato di equilibrio. La questione è meno chiara in Meccanica Quantistica: il collasso della funzione d’onda Y è irreversibile, ma il sistema formale (equazioni e relative soluzioni) è invariante rispetto all’inversione del tempo. Quindi tutte le teorie fondamentali comunemente accettate sono simmetriche rispetto all’inversione del tempo.
Fonte: http://www.superzeko.net/doc_eziof/EzioForneroSussidiDidattici/Il_rendimento_delle_macchine_termiche.doc
Sito web da visitare: http://www.superzeko.net/
Autore del testo: E.Fornero
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve