Disegno geometria piana

DISEGNO TECNICO
FONDAMENTI DI GEOMETRIA PIANA

Si comincia ad utilizzare i rapidograph eseguendo facili esercizi molto importanti sotto il profilo geometrico. Per convenzione, in rosso è riportato il pennino 0,2 ed in nero quello 0,4.

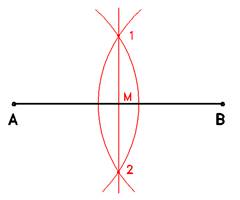
Costruzione della mediana di un segmento

Dato un segmento AB, tracciare con il compasso due porzioni di circonferenza puntando sia in A che in B con la medesima apertura, opportunamente maggiore della metà.
Le intersezioni 1 e 2 delle due porzioni di circonferenza individuano una retta mediana, ovvero passante per un punto M, medio, eqiuidistante dai punti A e B.
In geometria, A e B sono detti polari rispetto la mediana, che quindi è il luogo geometrico dei punti equidistanti da i poli

Costruzione della perpendicolare in un punto

Data una retta r ed un punto P ad essa appartenente per cui si voglia trovare una perperndicolare,  tracciare un semicerchio puntando il compasso nel punto P, ottenendo le intersezioni indicate con 1 e 2.
Puntando il compasso in 1 e 2 con apertura maggiore, si ottiene l'intersezione 3.
Congiungendo l'intersezione 3 con il punto P si ottiene una retta perpendicolare alla retta r nel punto P.

  Costruzione della parallela per un punto assegnato P

Data una retta r ed un punto P, segnare su r un punto 1, arbitrariamente scelto.
Tracciare con apertura 1-P una porzione di circonferenza fino ad intersecare r in un punto che chiameremo 2.
Senza mutare apertura, tracciare puntando in 2 (o in P) un'altra porzione di circonferenza. Questa passerà in entrambi i casi per il punto 1.
Registrare sul compasso la distanza 2-P, e con tale apertura riprodurre questa misura puntando in 1 il compasso. Verranno  
così a generarsi i punti 3 (o 4), per i quali passa la retta parallela
                                                              ad r e passante per P

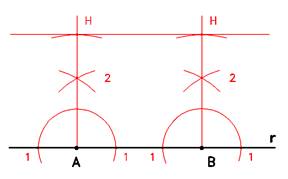Costruzione della parallela a distanza assegnata H

Data una retta r, scegliere arbitrariamente due punti A e B, opportunamente distanti.
Applicare il metodo delle perpendicolari (puntando in A ed in B il compasso ad apertura arbitraria, e generando due semicirconferenze; puntare nei punti 1 con apertura maggiore individuando i punti 2, per cui passano le perpendicolari alla retta r nei punti A e B.)
Registrare sul compasso la distanza prefissata e riportarla sulle perpendicolari fino a trovare i punti H, per i quali passa
la retta parallela alla retta r.

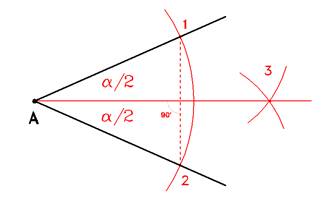La bisettrice

Dato un angolo a di cui si voglia trovare la bisettrice, puntare in A con apertura arbitraria, fino a trovare sulle rette che delimitano l'angolo a, i punti 1 e 2.
Con apertura maggiore, puntare sia in 1 che in 2 tracciando delle porzioni di circonferenza tali da intersecarsi individuando così il punto 3.
la congiungente tra A ed il punto 3 è detta retta bisettrice, in quanto divide l'angolo in due parti uguali.
NOTA: La bisettrice è anche mediana della corda 1-2 e dell'arco da essa sotteso.

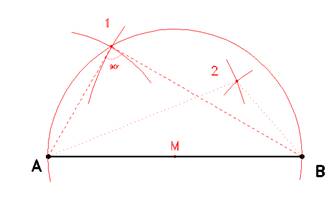Triangolazioni

Per posizionare nel piano un punto (1 o 2) tale da formare un triangolo rispetto ad un segmento AB, ed essendo note le misure dei cateti, basti puntare in A con apertura pari ad un cateto, ed in B con la misura dell'altro. L'intersezione delle due circonferenze individuano in modo univoco il terzo punto.
NOTA: Nel caso dei triangoli rettangoli, è da notare come il terzo punto appartiene alla circonferenza di centro M (punto medio di AB), e di raggio AB/2.
NOTA: Nel rilievo architettonico, la triangolazione è l'unico modo valido per avere una perfetta riproduzione
                                                                            delle reali disposizioni degli oggetti.

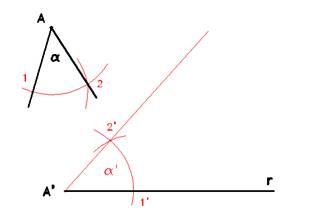Riproduzione di un angolo

Dato un angolo a ed una retta r sulla quale rintracciare il medesimo angolo, puntare il compasso con apertura arbitraria ed opportunamente ampia nel vertice A, intersecando in due punti che chiameremo 1 e 2.
Sulla retta r, segnare un punto A' e riprodurre la precedente apertura fino a rintracciare il punto 1'.
Tornando all'angolo a, registrare sul compasso la distanza 1-2, e riprodurla sulla retta r puntando in 1', trovado così il punto 2'.
La congiungente A'2' contiene rispetto a r la medesima porzione di piano di a.

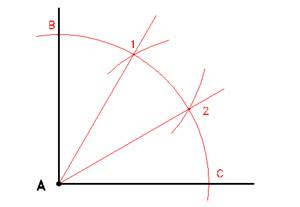Divisione di un angolo retto in tre parti

Dato un angolo retto, tracciare ad apertura arbitraria e puntando nel vertice A una porzione di circonferenza fino a trovare i punti B e C.
Con la medesima apertura puntare sia in B che in C ottenendo le intersezioni rispettivamente 2 e 1.
Le congiungenti A-1 ed A-2 dividono l'angolo retto in tre parti uguali da 30° ciascuna.
NOTA: i punti 1 e 2, dividono in tre anche l'arco, e le distanze B-1, 1-2 e 2-C sono uguali.

Costruzione delle tangenti ad una circonferenza

Data una circonferenza di centro C ed un punto esterno A da cui tracciare le tangenti, congiungere il punto A con il centro C (per individuare il centro, basti puntare in due punti della circonferenza con medesima apertura del suo raggio).
Tramite il metodo delle mediane rintracciare il punto medio M.
Con apertura M-C, puntando in M, tracciare una porzione di circonferenza tale da intersecare la circonferenza data in due punti che chiameremo T.
Le congiungenti A-T sono entrambe tangenti la circonferenza rispetto ad un punto dato.
Si noti come il triangolo ACT sia rettangolo in T, che quindi il raggio nel punto di tangenza sia sempre perpendicolare alla tangente.
Si noti anche che l'asse CA è mediana della corda TT e bisettrice dell'angolo di vertice in A.
Tangenti equatoriali si avrebbero se A giacesse all'infinito.

Il principio di Talete

Di notevole importanza per le fondamenta della geometria, nonchè della teoria della proiezione è il teorema di Talete.
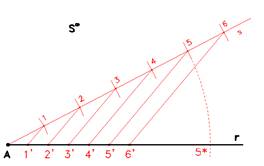Tracciare una retta r, e partendo da un punto A, tracciare una retta s arbitrariamente ed opportunamente inclinata rispetto ad r. Segnare dei punti ad intervalli regolari sulla retta s, in figura i punti 1, 2, 3, 4, 5, 6.
Scegliere un'inclinazione (*) e tracciare parallelamente tra loro dei segmenti passanti per i punti 1, 2, 3, 4, 5, 6, fino ad intersecare la retta r, generando le intersezioni 1', 2', 3', 4', 5'. 
Si noti come le misure dei segmenti proiettati siano inferiori rispetto al vero (osservare 5' e 5*), ma anche che il rapporto delle loro distanze è costante, tutto per effetto della proiezione da una sorgente impropria S , posizionata all'infinito.

(*) tale inclinazione offre proiezioni non aberrate se parallela alla corda 5-5*, ovvero perpendicolare alla bisettrice dell'angolo contenuto tra r ed s.

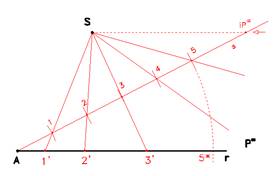
Il principio di Talete con sorgente propria

Proiettando da un punto proprio S gli intervalli 1, 2, 3, 4, 5, 6 sulla retta r, generando i punti 1', 2', 3', 4', .. noteremo una crescita progressiva delle distanze dovuta alla proiezione da sorgente propria.
NOTA: Nel caso di una sorgente propria S, le rette proiettanti non sono più parallele tra loro (fascio improprio), bensì convergenti nella sorgente prefissata (fascio proprio).
Se ne deduce che se la sorgente S si allontanasse all'infinito, allora il fascio proiettante diventa improprio e le rette proiettanti diventano tra loro parallele.
NOTA: Proiettando infine da S in maniera parallela ad r, rintracceremmo sulla retta s l'immagine di un punto P giacente all'infinito lungo la retta r.
A titolo informativo tali relazioni tra elementi di una proiezione sono dette corrispondenze.
NOTA: La vera posizione ad esempio del punto 5 su r si ottiene solo ribaltando il punto 5 rispetto il punto A, che in geometria è detto il punto unito, ottenendo così il punto 5*.