I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Lo sviluppo evolutivo dell'umanità fu determinato dal linguaggio e dalla sua capacità di elaborare un sistema di regole logiche (grammatica) che permisero di creare una "madre lingua" o particolari "lingue" . Il linguaggio grafico fu una delle prime forme di comunicazione dell'umanità, da cui scaturirono direttamente molte lingue ideografiche scritte come quella egiziana, cinese, ecc..
La nascita e lo sviluppo delle “lingue” hanno sempre avuto delle motivazioni di carattere ideologico, religioso, politico-economico e culturali e pochi individui venivano coinvolti, perché la " lingua" era uno strumento necessario per rappresentare e comunicare la conoscenza; per cui i poteri religioso, politico utilizzava la "lingua" come strumento di controllo e di consolidamento del loro potere.
Nell'antico Egitto gli scribi erano una casta privilegiata di funzionari e/o intellettuali al servizio dei Faraoni ed era a loro proibito diffondere o insegnare la "lingua" al di fuori della loro casta ed in particolare tra le classi inferiori e sottomesse al potere dei Faraoni.
L'antica segretezza che avvolgeva la "lingua", purtroppo, ancora oggi persiste nell'uomo, che la utilizza come segno di potere, di appartenenza ad un gruppo o come merce. Per fortuna accanto a queste forme di "lingue" chiuse o copyright vi sono esempi di "lingue" aperte o copyleft, che si basano sulla non mercificazione e sul libero scambio delle comunicazioni. Esempio di linguaggio copyleft è il sistema operativo LINUX.
Con la creazione delle "lingue naturali" non venne meno l'importanza del linguaggio grafico, che continuò ad esistere ed evolversi, generando altre "lingue", con delle grammatiche più o meno logiche e definite, ciò dipendeva dalle esigenze, motivazioni e conoscenze acquisite.
Anche nel campo artistico-pittorico vi furono e continuano ad esserci proposte di "grammatiche" o regole di rappresentazione grafiche, che alcune volte hanno dato origine a movimenti artistici legati al potere politico. La creatività artistica pur utilizzando delle regole di rappresentazione non può esprimersi mediante una lingua completamente codificata, ma ha necessità di avere delle libertà per meglio comunicare la soggettività e i valori culturali e umani dell’artista. Pertanto nel campo artistico il linguaggio grafico pur basandosi su alcuni criteri di rappresentazione è auspicabile che non si trasformi in lingua.
Mentre, l'esigenza di avere una precisa rappresentazione di un manufatto da realizzare venne avvertita anche dalle passate civiltà, perché era evidente che una buona rappresentazione grafica di un prodotto era una delle condizioni necessarie per la sua fattibilità. Nell'evoluzione delle tecniche di rappresentazione grafica di un manufatto, che hanno dato origine al "disegno tecnico", sono ben presenti i binomi disegno/progetto, forma/funzione, prodotto/produzione, scienza/tecnica, ecc., e di come lo svilupparsi di tali binomi ha permesso di trasformare il disegno delle macchine del XVII secolo nell'attuale disegno tecnico, che è una lingua in cui sono ben codificate le informazioni (forma, progetto, ecc.) riguardanti l'intero processo di progettazione/produzione di un prodotto.
Fu con la rivoluzione industriale del XVIII secolo che le esigenze di produzione e di organizzazione del lavoro imposero l'introduzione di precise e condivise regole per il "disegno tecnico", che non poteva più dipendere solo dalle capacità artistiche del progettista-disegnatore.
Una data che segna l'introduzione delle prime regole razionali riguardanti il Disegno Tecnico è il 1794, anno in cui fu pubblicato il libro " La Géometrie Descriptive" di Gaspard Monge ( 1746-1818).
L'anno precedente ( 1793) G. Monge pubblicò un altro importante libro " Description de l'art de fabriquer les canons" in cui già veniva illustrato il suo metodo della doppia proiezione ortogonale. Il metodo consisteva nel proiettare ortogonalmente un oggetto tridimensionale su due piani, uno orizzontale e l'altro verticale, ottenendo così due proiezioni che venivano chiamate , rispettivamente, pianta ed elevazione. Con il ribaltamento di 90° del piano verticale attorno alla retta intersezione tra i due piani di proiezione si otteneva un disegno di un oggetto costituito da due proiezioni che erano in relazione tra di loro.
Forse fu proprio la semplicità del metodo della doppia proiezione a determinare una rivoluzione nella tecnica del disegno, soprattutto nel settore dell'ingegneria militare, con la conseguenza che tale metodo fu ritenuto per molti anni un segreto militare da non divulgare. Infatti i primi studi di Monge sulla geometria descrittiva e l'applicazione dei suoi risultati al disegno tecnico risalgono al 1775.
La riservatezza del metodo venne ben espressa dall'architetto T. Jefferson, futuro presidente degli Stati Uniti ed ambasciatore a Parigi ai tempi di Luigi XVI, che in nota riservata scriveva " sul metodo francese di costruire cannoni : così esattamente simile che ciò che appartiene ad uno può essere usato per ogni altro".
Dopo la " La Géometrie Descriptive " di G. Mongevennero pubblicati molti manuali di geometria descrittiva da parte di numerosi allievi di G. Monge e polytechniciens furono chiamata gli autori di tali manuali. Alcuni di questi manuali ebbero enorme diffusione, come il manuale di S.F. Lacroix ( 1765-1843), che ebbe ben venticinque edizioni in un periodo di 90 anni.
Questi manuali contribuirono a dare delle basi matematiche al nostro Disegno Tecnico, essi si diffusero in molti settori non solo industriali e condizionarono anche il Disegno Architettonico. Nel 1824 venne pubblicato "Art de l'ingénieur" di B. Brisson, in cui gli aspetti artistici del disegno venivano di molto ridimensionati e si riconosceva l'utilità della "geometria descrittiva" di G. Monge nel Disegno.
[ Noto storica: G. Monge fu tra i fondatori e docente dell' école Polytechnique di Parigi ( 1794). Docenti di matematica di tale scuola furono : Lagrange e Laplace, che parteciparono attivamente alla Rivoluzione Francese insieme agli altri matematici come Legendre, Lazare Carnot, Condorcet, ecc.. Purtroppo qualcuno di loro fu vittima del terrore rivoluzione, come Condorcet che tra l'altro come Presidente dell'Assemblea Legislativa propose un progetto di Scuola Pubblica gratuita, che venne realizzato dopo il suo suicidio avvenuto il giorno dopo il sua arresto nel 1794. Mentre L. Carnot fu mandato in esilio da Napoleone, perché nel difendere gli ideali repubblicani della Rivoluzione si oppose a Napoleone. ]
Anche in Italia furono pubblicati testi di Geometria Descrittiva i cui contenuti si rifacevano ai libri di G. Monge. Tra questi ricordiamo il testo di C. Burali Forte , che venne pubblicato nel 1921 ed era suddiviso in due volumi ( Vol. I - Assonometria, Vol. II - Proiezioni quotate, Proiezioni di Monge, Prospettiva), i testi di Gino Loria su Storia della geometria descrittiva (1921) e Complementi di Geometria Descrittiva (1924), ecc..
Lo stretto rapporto che esiste tra Geometria Descrittiva e Disegno Tecnico era ben evidente a Monge, che nell'introduzione al suo testo riporta :
" La Géometrie descriptive a deux objets principaux: le premier, de donner les méthodes pour représenter sur une feuille de dessin qui n'a que deux dimensions, savoir, longueur et largeur, tous les corps de la nature qui en ont trois, longueur, largeur et profondeur, pourvu néanmoins que ces corps puissent être définis rigoureusement.
Le second object est de donner la manière de reconnaître, d'après une desciption exacte, les formes des corps, et d'en déduire toutes les vérités qui résultent et de leur forme et de leurs positions respectives. …"
Il precedente rapporto era più evidente in Burali-Forte, che nella prefazione al suo I volume di Geometria Descrittiva riporta " l'Assonometria … è strumento indispensabile per la rappresentazione d'insieme, o di dettaglio, delle macchine, per il taglio delle pietre e dei legnami; e poiché, essa può essere ridotta a forma teorica e grafica semplicissima, e dà, inoltre, una rappresentazione chiara e prossima alla visione ordinaria, è naturale che sia premessa alle altre specie di rappresentazione. "
Attualmente, il "Disegno Tecnico" è da considerarsi una “lingua” e la sua grammatica è rappresentata da ben definite norme , emanate da enti nazionali ( UNI, DIN, ANSI, ecc.) ed internazionali ( ISO, CEN, ecc.).
Resta, comunque, che la parte più importante del Disegno Tecnico è la rappresentazione della forma degli oggetti tridimensionali, ciò si ottiene definendo prima un modello geometrico dell'oggetto e solo successivamente lo si può proiettare su uno o più superfici piane detti piani di proiezione, che sono il foglio di disegno, lo schermo di un computer, ecc..
Pertanto la conoscenza dei metodi di proiezione è fondamentale per chi vuole disegnare un oggetto anche mediante i sistemi CAD (Computer Aided Drafting). L'evoluzione dei sistemi CAD, a partire dalla loro prima utilizzazione negli anni ’60 , ha comportato una modifica dei metodi tradizionali del Disegno Tecnico e più in generale dei metodi di progettazione e produzione. Un risultato molto importante dei nuovi sistemi CAD/CAM ( Computer Aided Design/Computer Aided Manufacturing) e di aver introdotto una metodologia di integrazione tra attività e discipline che si erano formalmente separate; recuperando in parte una visione unitaria ed originaria del processo disegno/progettazione/produzione tipica del periodo pre-industriale, dove spesso era la stessa persona (artigiano/progettista) che disegnava, progettava e produceva e spesso commercializzava il prodotto.
Per un miglior utilizzo e gestione dei sistemi CAD è indispensabile avere buone conoscenze di geometria analitica, che possono anche meglio far comprendere alcune tecniche di disegno che si basavano sulle costruzioni grafiche.
Questi appunti cercano di recuperare i forti legami esistenti tra il disegno tecnico e la geometria analitica, e si collegano idealmente al libro “La Géometrie Descriptive" di G. Monge con un Capitolo dedicato alla Geometria Descrittiva. Inoltre gli appunti sono finalizzati ad introdurre l’allievo allo studio della “computation geometry” che insieme alla computer graphics hanno permesso lo sviluppo dei sistemi CAD.
Capitolo I
PROIEZIONI
1.1 Definizione di proiezione
Nel disegno una proiezione è una trasformazione geometrica da uno spazio tridimensionale (3D) in uno spazio bidimensionale (2D). Dato un punto PÎObÌÂ3 , che appartiene all'oggetto Ob , è possibile calcolare la sua proiezione P' su un piano P ÍR2 mediante la funzione
P'=f(P, parametri della proiezione)
I parametri di una proiezione sono: il "punto di vista" o centro di proiezione, il "piano di proiezione" e l'oggetto.
La retta che passa per un generico punto PÎOb ed il centro di proiezione (PV) è detta "retta di proiezione" o raggio di proiezione. Tale retta interseca il piano di proiezione P in un punto P' , che rappresenta la proiezione o immagine del punto P.
Matematicamente, la determinazione della proiezione di un punto consiste nel calcolare la soluzione di un sistema di equazioni , costituito dalle equazioni della retta e della superficie di proiezione. In generale la superficie di proiezione è un piano, ma si potrebbe anche assegnare una superficie non piana come quella sferica, è ovvio che una tale proiezione è poco pratica perché il supporto di ogni proiezione è piano.
Se si esegue la proiezione per tutti i punti di PÎOb, si ottiene un insieme di punti Im, che definiamo immagine o proiezione di Og e tale che P'ÎImÌP.
Si osserva che facendo variare uno o più parametri della proiezione si ottengono differenti immagini dello stesso oggetto. Ad esempio se il punto di vista tende all'infinito le linee di proiezione convergono all'infinito e quindi sono parallele tra di loro.
E' possibile avere una prima classificazione delle proiezioni in base alla posizione del punto di vista PV rispetto all’oggetto. Se tale punto sta a distanza finita da P, tutte le sue rette di proiezione convergono verso il punto di vista, e la proiezione è detta prospettica o prospettiva. Se il punto di vista PV sta all'infinito la proiezione è detta parallela. Analizzando l'immagine prospettica di un oggetto, si ha che le sue dimensioni sono più piccole di quelle dell'oggetto se la distanza del piano di proiezione da PV e minore della distanza tra l'oggetto e PV; inoltre se PV è situato tra l'oggetto ed il piano di proiezione l'immagine risulta anche capovolta.
La geometria proiettiva ben descrive le proiezioni prospettiche e alcune proprietà dell’oggetto che possono risultare invarianti durante la trasformazione. Lo studio delle invarianti fu il tema principale delle ricerche geometriche nel XIX secolo. Molte proprietà geometriche variano durante la proiezione come quella del parallelismo, per cui se due spigoli dell'oggetto sono paralleli le corrispondenti immagini prospettiche non lo sono.
Le proiezioni prospettiche sono utilizzate nel disegno architettonico e in quelle applicazioni dove si vuole avere immagini reali dell'oggetto. Infatti la nostra visione della realtà non è altro che una rappresentazione prospettica, dove il piano di proiezione è la retina dell'occhio.
Viceversa, per un'assegnata direzione delle rette di proiezione, l'immagine che si ottiene di un oggetto con la proiezione parallela è la stessa su tutti i piani di proiezione tra di loro paralleli. Come vedremo in seguito, la proiezione parallela conserva il parallelismo tra entità lineari ma non la loro inclinazione. La conservazione dell'inclinazione vale solo per le entità dell'oggetto che sono parallele al piano di proiezione.
Inoltre, è interessante osservare che nella proiezione parallela se uno spigolo dell'oggetto è parallelo al piano di proiezione, esso conserva la sua lunghezza quando è proiettato.
Le proiezioni prospettiche non sono utilizzate nel Disegno Tecnico per cui non andremo a trattarle, mentre è necessario classificare ulteriormente le proiezioni parallele.
1.2 Classificazione delle proiezioni parallele
Le linee di proiezione sono caratterizzate da una direzione, a cui è possibile associare un versore l; mentre il piano di proiezione può essere univocamente determinato da un suo punto e dalla sua normale n.
Con la proiezione parallela il piano di proiezione può essere caratterizzato solo dalla sua normale n , poiché l'immagine dell’oggetto non varia se i piani di proiezione sono tra di loro paralleli.
Quando i versori l e n sono paralleli tra di loro la proiezione è detta "proiezione ortogonale" o assonometrica; viceversa quando i precedenti due versori non sono paralleli si ha una “proiezione obliqua”.
Teoricamente l'angolo tra i versori n e l potrebbe assumere qualsiasi valore compreso nell'intervallo [0,90°], ma si osserva che se l'angolo tende a 90° anche alcune dimensioni dell'immagine tendono ad avere valori infiniti. Ad esempio, se i due versori l e n sono tra di loro perpendicoli, la lunghezza dell'immagine di uno spigolo dell'oggetto, non parallelo al piano di proiezione, assume valore infinito.
Nel Disegno Tecnico le proiezioni oblique sono poco diffuse e le norme considerano solo due possibili angoli a tra l e n, che sono 30°,45° e 60°. Quando l'angolo è a=45° la proiezione obliqua è detta “cavaliere”.
Per comprendere la proiezione obliqua è sufficiente osservare l'ombra (immagine) del nostro corpo quando è illuminata dai raggi del Sole. La distanza del Sole dalla Terra è tale che si possono considerare i raggi del Sole come rette di una proiezione parallela. I parametri di tale proiezione sono i raggi del sole ( linee di proiezione), la superficie terrestre ( piano di proiezione) ed il nostro corpo.
Quando i raggi sono perpendicolari alla superficie si ottiene un'ombra che è l'immagine del nostro corpo ottenuta con una proiezione ortogonale, per altre inclinazioni si ha un'ombra che è una proiezione obliqua, al tramonto o all'alba tale ombra tende ad avere una lunghezza infinita.
Le proiezioni ortogonali ( assonometriche ) sono principalmente utilizzate nel Disegno Tecnico, che come vedremo possono essere infinite perché occorre considerare tutte le possibili posizioni relative tra l'oggetto e il piano di proiezione.
Per meglio analizzare le posizioni relative tra oggetto e piano di proiezione è opportuno considerare l'oggetto in una posizione fissa associando ad esso un sistema di riferimento di assi cartesiani per cui il versore del piano di proiezione sarà riferito a tale sistema di riferimento.
La scelta del sistema di riferimento, anche se è soggettiva, deve rispettare alcuni criteri razionali ed in particolare quello di semplificare la descrizione matematica dell'oggetto. Ad esempio se l'oggetto è un parallelepipedo, il sistema di riferimento più naturale è quello di associare ai suoi tre spigoli principali un sistema di riferimento cartesiano. Potremmo definire anche un altro sistema di riferimento cartesiano, ma sicuramente la descrizione matematico-geometrica dell'oggetto sarebbe più complicata.
In generale un buon sistema di riferimento cartesiano associato ad un oggetto ha almeno un asse e/o un piano principale paralleli ad assi e superfici piane dell'oggetto, o più in generale deve facilitare la descrizione matematica delle caratteristiche ( linee, superfici, ecc.) dell'oggetto. Se l'oggetto è abbastanza complesso o composto da più parti è possibile definire per ogni parte dei sistemi di riferimenti locali .
Rispetto ad un sistema di riferimento cartesiano, il piano di proiezione è individuato dal versore della sua normale n =(nx,ny,nz), in particolare da due sue componenti, perché la terza è dipendente dovendo essere soddisfatta la relazione
![]() (1.1)
(1.1)
Poiché due componenti di n possono assumere infiniti valori, ne consegue che è possibile avere infinite proiezioni ortogonali.
Quando il piano di proiezione è parallelo ad uno dei piani principali del sistema cartesiano, la proiezioni che si ottiene è detta " proiezione ortografica".
Se si considera anche il verso ( + e -) di proiezione, si osserva che esistono ben 6 distinte proiezioni ortografiche. In questi casi il versore n ha una componente uguale in valore assoluto ad 1 e le altre due sono uguali a zero.
Ad esempio, il piano di proiezione avente n=(0,1,0) rappresenta una proiezione ortografica su un piano parallelo al piano xz nella direzione opposta al versore associato all'asse y. I sei versori di n a cui corrispondono le sei proiezioni ortografiche sono :
(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1), (0,0,-1).
Se il piano di proiezione non è parallelo ad un piano principale del sistema di riferimento cartesiano associato all'oggetto si ha una proiezione che è detta "proiezione assonometrica". Per motivi di classificazione si è ritenuto opportuno di utilizzare il termine di proiezione assonometrica solo a quelle proiezioni il cui piano di proiezione non è parallelo ad uno dei piani principali. In diversi testi e come abbiamo anche noi detto in precedenza, spesso tutte le proiezioni parallele ed ortogonali vengono chiamate proiezioni assonometriche.
Mentre si possono avere solo 6 proiezioni ortografiche, viceversa il numero delle proiezioni assonometriche che si può avere è infinito. Infatti è possibile orientare il piano di proiezione in infiniti modi, ovvero si possono assegnare a due componenti del versore n infiniti valori compresi nell'intervallo aperto ]-1,1[.
Le norme prevedono solo tre possibili proiezioni assonometriche : le isometriche, le dimetriche e le trimetriche. La differenza principale tra i tre tipi di assonometrie dipende dalla riduzione che subiscono i tre versori principali quando vengono proiettati ortogonalmente sul piano di proiezione.
Nella proiezione isometrica la normale al piano di proiezione ha componenti uguali in valore assoluto, per cui i tre versori principali del sistema cartesiano presentano la stessa inclinazione rispetto al piano di proiezione e la loro lunghezza subisce la stessa riduzione quando viene proiettata.
Quesito: Quante sono le possibili proiezioni isometriche?
La risposta a questo quesito verrà data in modo analitico più avanti.
Nella assonometria dimetrica solo due versori principali subiscono la stessa riduzione , mentre nella assonometria trimetrica i tre versori principali subiscono differenti riduzioni.
In Fig. 2 è riportata una classificazione delle proiezioni.
Come abbiamo detto in precedenza, le proiezioni utilizzate nel Disegno Tecnico sono quelle ortogonali, infatti lo stesso G. Monge dava la seguente definizione di proiezione : " On appelle projectionda'u point sur un plan, le pied de la perpendiculaire abaissée du point sur le plan"; che rappresenta una proiezione ortogonale.
Nella progettazione industriale al posto del termine "oggetto" o altro sinonimo si utilizza spesso il termine "prodotto" , che ben si collega all'inglese "product" ( Product Design., Product Development).
1.3 Definizioni ed operazioni elementari sui vettori
Un punto P=(x,y,z) in un sistema tridimensionale di assi cartesiani CS=(0;x,y,z) è individuato dai valori delle tre coordinate o componenti del vettore posizione
r=OP=xi+yj+zk (1.2)
dove i, j e k sono i versori associati rispettivamente agli assi x, y e z.
Le tre componenti del vettore r =(x,y,z) non sono altro che le proiezioni ortogonali del vettore r sui tre assi principali.
Un vettore è caratterizzato da un'origine, da una direzione orientata (verso) e da una lunghezza. Un vettore avente lunghezza zero è chiamato vettore nullo, a tale vettore non è possibile associare una direzione.
![]()
La lunghezza o modulo del vettore r è uno scalare che si può ottenere dal teorema di Pitagora
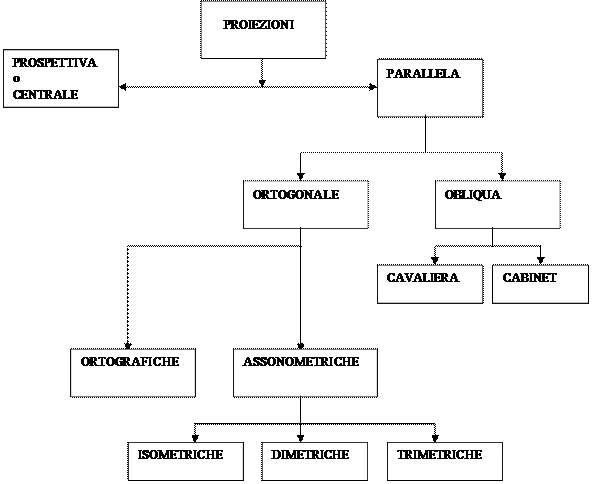
Fig. 1.2: Classificazione delle proiezioni
Il vettore unitario o versore di r nella direzione OP è il vettore
![]() (1.3)
(1.3)
Due vettori r1=( x1,y1,z1) e r2=(x2,y2,z2) sono uguali solo se tutte le corrispondenti componenti lo sono
r1= r2 ↔ (x1= x2 , y1= y2 , z1 =z2 )
La somma o differenza tra due vettori si ottiene sommando o sottraendo le corrispondenti componenti, graficamente la somma tra vettori si ottiene applicando la regola del parallelogramma
r = r1 ± r2 = ( x1±x2, y1±y2, z1±z2 ) (1.4)
La moltiplicazione tra uno scalare l ed un vettore r =(x,y,z) da un vettore avente la stessa direzione e senso di r ma il suo modulo è uguale a lïrï
l r = (l x, ly, lz) (1.5)
Il prodotto scalare tra due vettori r1=( x1,y1,z1) e r2=(x2,y2,z2) è uno scalare il cui valore è dato da
![]() (1.6)
(1.6)
dove a è l'angolo tra r1 e r2.
Il prodotto scalare tra due vettori perpendicoli è zero, mentre se sono paralleli il prodotto scalare non è altro che il prodotto tra i loro moduli.
La (1.6) è molto importante sia per calcolare l'angolo tra due vettori sia per calcolare la proiezione ortogonale di un vettore su un'assegnata direzione. Infatti se u2=r2 è un versore si ha che il precedente prodotto scalare rappresenta la lunghezza della proiezione ortogonale di r1 sulla retta avente direzione u2.
![]() (1.7)
(1.7)
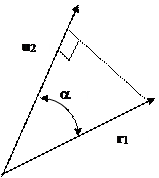
Fig. 1.3: Proiezione ortogonale di un vettore su una retta orientata u2 .
Se consideriamo i versori i= (1,0,0), j=(0,1,0) e k=(0,0,1) si ha
i.i=j.j=k.k=1 , i.j=j.k=k.i=0
Il prodotto scalare tra vettori permette di scrivere in forma più compatta il modulo somma o differenza tra due vettori che è dato da
![]()

 r1
r1![]()
![]()
![]()
![]()
r = r1 + r2 r = r1 - r2
Fig. 1.4 : Somma e sottrazione di vettori.
![]() (1.8)
(1.8)
che rappresenta la legge dei coseni già nota agli antichi greci.
Nel caso di una sommatoria tra n vettori ri per i=1,..,n è possibile generalizzare la precedente formula ottenendo
![]() (1.9)
(1.9)
Vedremo in seguito che la (1.9) contiene come caso particolare anche il teorema generalizzato di Carnot, che si ottiene quando n=3.
Il prodotto vettoriale tra due vettori r1=( x1,y1,z1) e r2=(x2,y2,z2) è un vettore perpendicolare al piano formato da r1 e r2 ed è dato da
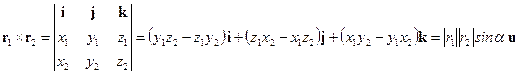 (1.10)
(1.10)
dove u è il versore normale al piano formato da r1 e r2 .
Per conoscere il senso del versore u è sufficiente applicare la regola della mano destra dove il pollice indica r1, l'indice r2 ed il medio indica il senso del versore u.
Mentre il prodotto scalare tra un vettore ed una retta orientata permette di calcolare la sua proiezione ortogonale sulla retta, viceversa il prodotto vettoriale tra un vettore e una retta orientata da la componente del vettore in direzione perpendicolare alla retta. Infatti se u2 = r2 è il versore associato alla retta orientata si ha
![]()
![]()
da cui si ottiene la seguente relazione
![]() (1.11)
(1.11)
Altre proprietà del prodotto vettoriale sono
![]()
i x i = j x j = k x k = 0 i x j= k , j x k = i , k x i = j
Le precedenti equazioni permettono di calcolare il prodotto vettoriale, ottenendo l'equazione (1.10)
r1 x r2 = (x1i+y1j+z1k) x ( x2i+y2j+z2k)=( y1z2- y2z1)i +( x2z1- x1z2)j+( x1y2- x2y1)k
Se r3=(x3, y3 , z3 ) è un terzo vettore, il triplo prodotto scalare è dato da
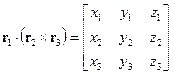 (1.12)
(1.12)
Se si effettua una ciclica permutazione delle righe del determinante il suo valore non cambia, pertanto
r1 . (r2 x r3 ) = r2 . (r3 x r1 ) = r3 . (r1 x r2 )
Se due vettori sono paralleli, ciò comporta che il determinante ha due righe proporzionali o uguali per cui il triplo prodotto scalare è nullo.
2. 4 Alcune applicazioni delle operazioni vettoriali
Un piano è univocamente definito se si considerano tre suoi punti non allineati. Per calcolare il vettore normale a tale piano è sufficiente considerare il prodotto vettoriale tra due vettori aventi per estremi i punti assegnati.
Problema 1.1: Calcolare la normale al piano passante per i tre punti P1=(1,2,0),
P2=(2,4,1) e P3=( 3,2,1) e l’area del triangolo avente per vertici tali punti.
Consideriamo i vettori P1P2= (2-1,4-2,1-0)=(1,2,1) e P1P3=(3-1,2-2,1-0)=(2,0,1), questi vettori appartengono ad un piano il cui vettore normale N è dato da

Il versore di N versore è
![]()
L’area del triangolo avente per vertici P1=(x1,y1,z1), P2=(x2,y2,z2), e P3=(x3,y3,z3) è uguale al semiprodotto di una sua base per la relativa altezza. Se H è la proiezione ortogonale di P3 su P1P2 , il vettore P3H rappresenta un’altezza del triangolo, per cui si ha
![]() (1.13.a)
(1.13.a)
E' preferibile associare all'area del triangolo un vettore ottenuto dal prodotto vettoriale (1.13.a), per cui la sua direzione risulta perpendicolare al piano del triangolo mentre il suo modulo è uguale all'area
 (1.13.b)
(1.13.b)
dove Ar,i , Ar,j Ar,k sono le componenti del vettore area del triangolo.
Il quadrato del modulo del vettore area risulta essere uguale a
![]() (1.14)
(1.14)
La (1.14) può essere considerata come la generalizzazione del teorema di Pitagora applicato ad una generica figura piana. Infatti è sempre possibile mediante triangolazioni avere una partizione della figura piana costituita dall'unione di triangoli complanari, per cui considerando le loro proiezioni si ha che la somma dei quadrati delle aree di una figura piana su tre piani perpendicolari è uguale al quadrato dell'area della figura.
Se i vertici del triangolo appartengono tutti al piano xy , l'unica componente diversa da zero è la k per cui la (1.13.b) si semplifica nella seguente formula, che fu proposta da Lagrange
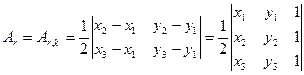 (1.15)
(1.15)


Fig. 1.5: Altezza di un triangolo.
[Nota storica: Nel 1802 sul Journal de l'E'cole Polytechnique venne pubblicata una memoria di Monge e Hachette intitolata Application d'algébre à la géométrie , che iniziava con la dimostrazione della generalizzazione del teorema di Pitagora per una superficie piana.]
L'aver associato un vettore all'area di un triangolo, permette di calcolare facilmente la sua proiezione ortogonale su un piano di proiezione di normale n. Infatti, se si calcola il prodotto scalare tra Ar, e n, si ottiene l'area dell’immagine del triangolo sul piano di normale n.
Se si considera un tetraedro, definito da quattro punti non complanari, risulta che la somma delle proiezioni ortogonale delle aree di tre triangoli sulla superficie del quarto triangolo è proprio uguale all'area di quest'ultimo; pertanto possiamo scrivere
![]() (1.16)
(1.16)
dove A, B,C e D sono i vettori area dei quattro triangolo che compongono il tetraedro, mentre nA, nB , nC e nD sono i corrispondenti versori normali. Gli angoli α, β, e δ sono rispettivamente le inclinazioni dei piani contenenti B, C e D rispetto al piano contenente A.
Un teorema riguardante le aree dei quattro triangoli di un tetraedro fu formulato anche da L. Carnot, che rappresenta una generalizzazione della legge dei coseni quando si considera la somma di tre vettori
![]() (1.17)
(1.17)
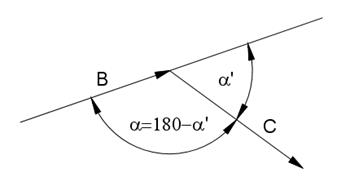
dove α, β, e δ sono, rispettivamente, gli angoli tra i piani contenenti i triangoli B e C, B e D , C e D.
Come è stato detto in precedenza, la formula di Carnot (1.17) si ottiene dalla (1.9) quando n=3, dove, per semplicità di notazione si è posto : A=r, B=r1, C=r2 e D=r3. I tre segni negativi che appaiono nella (1.17) sono dovuti al fatto che in tale formula gli angoli che si considerano sono quelli supplementari degli angoli definiti tra due vettori consecutivi, che si ottengono dal prodotto scalare, infatti
Fig. 1.6 :Angoli tra vettori
E' possibile generalizzare la (1.16) ed applicarla ad un poliedro qualsiasi costituito da facce triangolari, dove la normale alle superfici triangolari è rivolta verso l'esterno. Al pari di un poligono chiuso, la cui somma vettoriale dei lati è uguale a zero, anche per il precedente poliedro la somma vettoriale delle aree dei triangoli è nulla e ciò vale, ovviamente, anche per ogni sua proiezione.
Se il piano di proiezione contiene una faccia del poliedro, che indichiamo col vettore area A e se Ti ,i=1,..,n sono i vettori aree delle restanti facce triangolari del poliedro si ha
![]() (1.18)
(1.18)
Sempre considerando un generico tetraedro, si osserva che l'altezza relativa ad una sua base è data dal prodotto scalare tra il versore area della base e un vettore qualsiasi associato ad uno spigolo non appartenente alla base; pertanto se P1=(x1,y1,z1), P2=(x2,y2,z2), P3=(x3,y3,z3) e P4=(x4,y4,z4) sono i quattro vertici del tetraedro il suo volume è dato dal triplo prodotto scalare
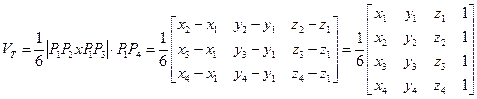 (1.19)
(1.19)
La precedente formula compatta fu ottenuta da Lagrange che la espose nel 1775 nel suo lavoro Solutions analytiques de quelques problémes sur les pyramides triagulaires.
In generale il volume di un generico prisma retto o non è dato dal prodotto scalare tra il vettore area di una base e un vettore spigolo non appartenente alla base.
Problema 1.2: Verificare le precedenti formule per il tetraedro avente i seguenti vertici P0=(0,0,0), P1=(x,0,0), P2=(0,y,0) e P3=(0,0,z). Inoltre, calcolare la normale del piano obliquo e le inclinazioni tra le facce.
I quattro punti determinano i sei vettori spigoli r1=P0P1=(x,0,0), r2=P0P2=(0,y,0), r3=P0P3=(0,0,z), r4=P1P2=(x,y,0), r5=P1P3=(x,0,z), r6=P2P3=(0,y,z).
Fig. 1.7: Tetraedro

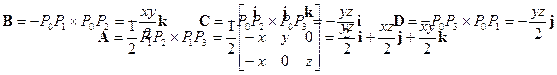
Tutti i vettori delle aree sono stati orientati verso l'esterno, per cui si verifica facilmente che A+B+C+B=0 . I versori normali ai piani contenenti le facce B, C e D sono banali, essendo rispettivamente nB=-k, nC=-i e nD=-j; mentre il versore di A è dato da
![]() (1.20)
(1.20)
Le inclinazioni tra le facce del tetraedro si ottengono considerando i prodotti scalari dei corrispondenti versori normali, nel nostro esempio il calcolo è semplice perché tre facce hanno la normale orientata secondo gli assi principali, pertanto se indichiamo con α, β, e δ gli angoli tra la faccia obliqua e le facce appartenenti ai piani xy, yz e zx si ha

Analogamente semplice è il calcolo del volume, dove molti termini del determinante (1.19) sono uguali a zero, per cui si ha
VT=xyz/6
1.5 Rapporti di riduzione nelle proiezioni ortogonali ed oblique.
Si consideri un generico vettore V in uno spazio (0;x,y,z) e la sua proiezione ortogonale su un piano di normale n.
E' possibile definire come rapporto di riduzione o fattore di riduzione il rapporto tra i moduli del vettore immagine e il vettore proiettato. Il modulo del vettore immagine si ottiene dal prodotto vettoriale tra V ed n, per cui il rapporto di riduzione in una proiezione ortogonale è dato da:
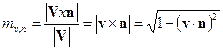 (1.21)
(1.21)
dove v è il versore di V.
Il rapporto di riduzione nella proiezione ortogonale è compreso nell'intervallo [0,1], è uguale a zero se V ed n sono paralleli, mentre è uguale a l se V e n sono perpendicolari, in quest'ultima condizione l'entità geometrica non subisce nessuna riduzione quando viene proiettata.
La precedente equazione può essere utile per risolvere il problema inverso, cioè assegnati dei rapporti di riduzione determinare il piano di proiezione, che è individuato dal suo versore normale. Il problema ammette infinite soluzioni se si assegna un solo rapporto di riduzione, perché abbiamo un sistema di due equazioni con le tre incognite n=(nx,ny,nz). Le due equazioni sono ottenute una dal rapporto di riduzione e l'altra è l'equazione quadratica che lega le componenti di un versore.
Per determinare uno o più piani di proiezione occorre assegnare il rapporto di proiezione di un altro vettore v2 non parallelo al primo v1, così avremo un sistema nonlineare di tre equazioni di secondo grado in tre incognite
 (1.22)
(1.22)
Per il teorema di Bezout il precedente sistema può avere un massimo di 8 soluzioni.
La formula del rapporto di riduzione si semplifica se al posto del generico versore v consideriamo i versori principali del sistema di riferimento: i=(1,0,0), j =(0,1,0) e k=(0,0,1). Per tali versori il loro prodotto scalare con il versore n non è altro che la corrispondente componenti del versore n. Pertanto, la (1.21) applicata ai versori principali diventa
 (1.23)
(1.23)
Le equazioni della (1.23) non sono tra di loro indipendenti, infatti la somma dei loro quadrati è
![]() (1.24)
(1.24)
pertanto, è possibile assegnare solo per due versori principali il rapporto di riduzione su un piano di proiezione.
Se si applicano le precedenti equazioni alla proiezioni ortografiche si osserva che due versori principali hanno un rapporto di riduzione uguali ad 1 mentre il restante ha il rapporto di riduzione uguale a zero.
La soluzione del problema inverso è semplice quando si assegnano i rapporti di riduzione di due versori principali, perché nel sistema di equazioni (1.23) ogni equazione ha una sola incognita, per cui
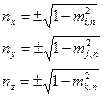 (1.25)
(1.25)
Ad esempio, se si vuole avere mi,n=1 e mk,n=1 , risulta per la (1.24 ) che mj,n= 0 ed i versori del piano di proiezione sono n=(0,±1,0)= ± j, cioè piani di proiezione paralleli al piano principale xz , il segno + o - indica i due sensi di proiezione rispetto al versore j.
Se si considera l'assonometria isometrica si ha che i rapporti di riduzione dei versori principali devono essere uguali, per cui dalla (1.24) si ha
![]()
I versori dei piani di proiezione nell’assonometria isometrica possono essere determinati o dalla (1.25) o semplicemente considerando che le componenti di n sono uguali in valore assoluto per cui
![]()
Si osserva che il numero delle combinazione dei segni + e - per le componenti del versore n sono 8, pertanto le possibile assonometrie isometriche di un oggetto sono 8.
Le norme UNI considerano anche le assonometrie dimetriche dove due versori principali presentano lo stesso rapporto di riduzione, in particolare tale rapporto è posto uguale a 0.94 da cui risulta che il terzo rapporto di riduzione deve essere uguale a 0.48.
Se si assume mi,n=0.94, mj,n=0.94 e mk,n= 0,48, gli 8 piani su cui si ha una proiezioni dimetrica sono
n= ( ±0.34, ±0.34, ± 0.87)
Anche per la proiezione obliqua possiamo determinare il rapporto di proiezione, ma per tale proiezione occorre assegnare una direzione di proiezione, che indichiamo con il versore l. Per determinare l'immagine di un vettore V sul piano di proiezione di normale n, consideriamo prima la proiezione sul piano di normale l, che è uguale al modulo del prodotto vettoriale tra V e l. Tale proiezione è il cateto di un triangolo rettangolo la cui ipotenusa è proprio l'immagine obliqua di V. L'angolo tra il cateto e l'ipotenusa è l'uguale al supplementare dell'angolo formato tra i versori l e n, il cui coseno è uguale al prodotto scalare l.n, da ciò deriva che l'immagine obliqua è dato dal rapporto |Vxn| / l.n, per cui
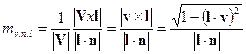 (1.26)
(1.26)
Nella proiezione obliqua il rapporto di proiezione è compreso nell'intervallo [0,∞[ , per cui la lunghezza dell'immagine può essere più grande della lunghezza reale dell'entità proiettata.
Anche nella proiezione obliqua il rapporto di riduzione è uguale a 1 se il versore v è parallelo al piano di proiezione. Infatti in tali casi i versori v e n sono perpendicolari per cui se si considerano le loro proiezioni ortogonali sulla retta di direzione l si ha la relazione
![]()
che sostituita nella (1.26) da per il rapporto di riduzione il valore 1.
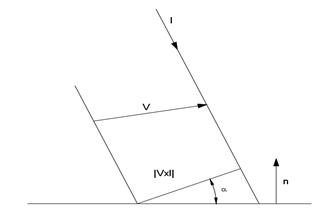
Fig. 1.8: Proiezione obliqua.
1.6 Formulazione parametrica di rette e piani.
L’introduzione dei sistemi CAD nei settori della progettazione e produzione industriale ha comportato la necessità di utilizzare la formulazioni parametrica per le curve e superfici, ciò permette una più facile manipolazione, analisi, rappresentazione, ecc. della forma geometrica degli oggetti.
Prima di esporre la formulazione parametrica delle curve ed in particolare delle rette, si illustreranno alcuni limiti delle tradizionali formulazioni esplicite ed implicite delle curve.
1.6.1 Formulazione esplicita ed implicita delle curve.
La retta è la più semplice curva e la sua equazione più familiare sul piano (x,y) è data da
y=mx+c (1.27)
deve m è la pendenza e c è l'intersezione della retta con l'asse y.
La (1.27) è l’equazione esplicita della retta e permette di calcolare la variabile dipendente y una volta assegnato il valore di x.
Purtroppo, questa semplice e diffusa formulazione non permette di rappresentare le linee verticali, come x=1.
Se si assegnano due punti P1(x1,y1) e P2(x2,y2), la retta che passa per questi punti è
![]()
o nella forma più simmetrica ![]() 1.28)
1.28)
La (1.28) è la forma implicita di una retta, perché y può essere calcolato, per un assegnato valore di x, solo risolvendo l’equazione. Lo stesso vale se si vuole calcolare x per un assegnato valore di y. Pertanto, nella (1.28) non esiste una variabile dipendente.
La formulazione implicita (1.28), diversamente dalla (1.27) permette di rappresentare le linee verticali, infatti se x2=x1 ed y2#y1 l'equazione della retta verticale è
x=x1
In generale, la formulazione implicita di una retta è data da
ax+by+c=0
che per b=0 rappresenta una retta verticale.
Le formulazioni esplicita ed implicita di una curva piana nel sistema bidimensionale (O ;x,y) sono rispettivamente
y=f(x) e g(x,y)=0 (1.29)
La forma esplicita è accettabile quando la curva ha un solo valore di y per ogni x e non presenta tangenti verticali. Purtroppo con tale formulazione non è possibile rappresentare importanti curve come l’ellisse. Ad esempio, l’equazione della circonferenza viene data, generalmente, nella formulazione implicita
![]()
Se si volesse la sua forma esplicita occorrerebbe dividerla in due parti, che corrispondono ai valori positivi e negativi delle ordinate
![]()
L’equazione della retta tangente ad una curva data in forma esplicita nel punto P1=(x1,y1), è data dallo sviluppo lineare della funzione (1.29) ottenendo
![]() (1.30)
(1.30)
Se la curva presenta una tangente verticale in P1 , la sua derivata assume valore infinito e ciò è un’ulteriore verifica della difficoltà ad operare con la formulazione esplicita.
Analogamente, lo sviluppo lineare della curva implicita g(x,y)=0 nel punto P1=(x1,y1), rappresenta l'equazione della tangente in tale punto ed è data
![]() (1.31)
(1.31)
Problema 1.3: Calcolare la tangente all'ellisse 2![]() nel punto P1=(1/3,4/3).
nel punto P1=(1/3,4/3).
Derivando l'equazione dell'ellisse si ha: ![]()
Dalla (1.31) si ha 2/3(x-1/3)+8/3(y-4/3)=0, che si semplifica nella : 3x+12y-17=0.
Il calcolo dell’equazione della retta normale si ottiene considerando che i coefficienti angolari sono opposti e reciproci a quelli della tangente, pertanto si ha
![]() e
e ![]()
1.6.2 Formulazione parametrica di una curva nello spazio.
Se le coordinate x, y e z sono funzione di un parametro ausiliario t, si ha la formulazione parametrica della curva, che è data da
x=x(t) y=y(t) z=z(t) a£t£b (1.32)
Ad esempio, la circonferenza di centro C=(0,0,0) e raggio R nel piano (x,y) può avere la seguente formulazione parametrica
![]()
Se il limite superiore del parametro t fosse stato posto eguale ad a avremmo definito un arco di circonferenza compreso tra 0 ed a.
Generalmente, si preferisce normalizzare il parametro t facendolo variare nell’intervallo tÎ[0,1], ciò si ottiene mediante una semplice trasformazione lineare.
![]()
Ad esempio se tÎ[a,b] il corrispondente parametro normalizzato t sarà data dalla trasformazione lineare
Nel nostro caso essendo a=0 e b=2p, l’equazione parametrica normalizzata della circonferenza diventa
![]()
La retta tangente alla curva parametrica (1.32) nel punto P1(x1,y1,z1), dove x1=x(t1), e y1=y(t1) e z1=z(t1) è data dallo sviluppo lineare delle componenti
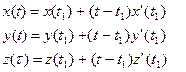
Problema 1.4: Calcolare la tangente e la normale all’ellisse di equazione x=2cos(2πt) , y=sin(2πt) nel punto P1=(sqrt(2),sqrt(2)/2) corrispondente al parametro t=1/8.
Poiché x’(t)=-4psin(2pt) e y’(t)= 2pcos(2pt), la retta tangente è data da
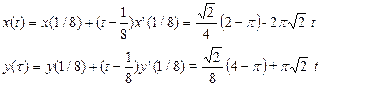
u
Una curva può presentare diverse formulazioni parametriche così come è possibile passare da una formulazione ad un'altra. La trasformazione che permette di ottenere una formulazione implicita da una parametrica viene detta "implicitizzazione", mentre la trasformazione inversa è detta "parametrizzazione".
Nel caso particolare di una retta passante per i punti P1(x1,y1,z1) e P2(x2,y2,z2) la sua equazione parametrica è data da
![]() (1.33)
(1.33)
Si osserva che tutti i punti del segmento P1P2 si ottengono facendo variare tÎ[0,1].
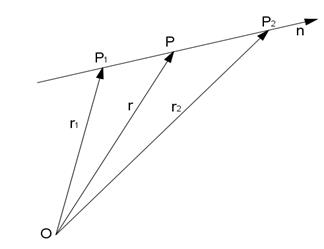
Associando a ciascun punto P=(x,y,z) il corrispondente vettore posizione r=0P=(xi,yj,zk), l’equazione della retta passante per i punti P1(x1,y1,z1) e P2(x2,y2,z2) può essere descritta in termini vettoriali. Infatti, considerando la Fig. 1.9 si ha : r1+P1P=r.
Il vettore P1P a meno di uno scalare t ha la stessa direzione del vettore P1P2 per cui si può porre P1P=tP1P2, pertanto l'equazione della retta è
r(t) = r1+ tP1P2= r1 + t (r2- r1)=(1-t) r1 +t r2 (1.34)
Se si esplicita la precedente equazione rispetto a ciascuna componente si ottiene la formulazione parametrica (1.33). Pertanto, la formulazione vettoriale di una curva rappresenta un modo più semplice e generale per esprimere la formulazione parametrica in uno spazio Rn.
Se invece dei due punti viene assegnato un punto ed un versore direzione n, l’equazione della retta è data da
r (t) = r1+t n.
Fig. 1.9 : Rappresentazione di una retta.
Problema 1.5 : Calcolare l’equazione della retta passante per il punto P1=(1,2,1) ed avente direzione N=(1,2,2).
Se si considera il versore di N si ha n=(1/3,2/3,2/3), pertanto l’equazione della retta è
r= (1,2,1)+ t n → x=1+t/3 , y=2+t 2/3 , z= 1+ t 2/3.
u
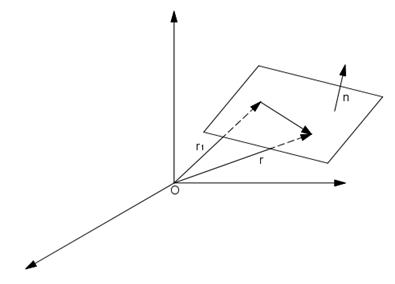
Utilizzando i vettori è possibile ottenere facilmente anche l’equazione di un piano passante per un assegnato punto P1 ed avente normale n.
Per ogni punto P appartenente al piano, il vettore P1P è normale a n, per cui il prodotto scalare P1P .n=0 ; poiché P1P =r- r1 , l'equazione del piano è
(r-r1).n =0 → r.n = x nx+ y ny + z nz = r1.n = p (1.35)
dove lo scalare p rappresenta la distanza del piano dall’origine.
Fig. 1.10: Equazione del piano (r-r1).n =0.
Dalla (1.35) si osserva che se f(x,y,z)=ax+by+cz+d=0 è l’equazione implicita del piano, le componenti del vettore normale al piano sono
![]()
Per calcolare la distanza del piano dall’origine occorre considerare il versore di N, pertanto abbiamo

Un piano può essere univocamente individuato anche quando sono assegnati tre suoi punti non allineati. In questo caso se indichiamo con r1, r2 e r3 i vettori posizione dei tre punti, la normale al piano è data dal prodotto vettoriali di due vettori giacenti sul piano. Se si considerano i vettori (r2- r1) e (r3- r1), la normale è data da N=(r2- r1)x (r3- r1), per cui il piano sarà
r.N =. ri .N
dove l'indice i può essere il valore 1, 2 o 3. E' preferibile sostituire ad N il suo versore n.
Problema 1.6: Calcolare la distanza del piano dall’origine passante per r1=(1,2,1) ed avente normale N=(1,2,2).
Considerando il versore di N, che è n=(1/3,2/3,2/3) dalla (1.35) si ha l’equazione del piano
![]()
![]()
per cui la distanza del piano dall'origine è uguale a 7/3.
1.7 Proiezione di punti su un piano e su una retta.
1.7.1 Proiezione ortogonale di un vettore su un sottospazio
La comprensione della definizione generale di proiezione ortogonale di un vettore su un sottospazio, permette di comprendere meglio l’esistenza di altre proiezioni ortogonali come quella di un punto su una retta, ecc..
Consideriamo lo spazio lineare ordinario Rn e un insieme ordinato di vettori U=(u1,u2,..,un), tali vettori è una base ortogonale di Rn se il prodotto scalare tra due qualsiasi vettori di U è zero
![]()
Se il vettore ui ha lunghezza unitaria la base è detta ortonormale.
I vettori di una base ortogonale sono linearmente indipendenti e ogni punto rÎRn , che è rappresentato dal vettore posizione OP, può essere espresso come combinazione lineare di U
![]()
dove O è l’origine da cui partono tutti i vettori della base.
La base ortonormale U e l’origine O costituiscono un sistema di coordinate ortonormale dello spazio Rn e il vettore a=(a1,a2,..,an) sono le coordinate del punto r, che sono uguali rispettivamente ai prodotti scalari
ai=r.ui i=1,2,..,n
Sia V=(v1,v2,..,vn) un’altra base ortonormale di coordinate i cui vettori sono dati da

Le coordinate dello stesso punto r rispetto a V sono date dai prodotti scalari
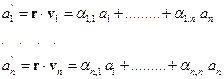
Le precedenti equazioni possono essere espresse nella forma matriciale
![]()
dove A è la matrice di trasformazione, che ha la proprietà di essere una matrice ortogonale, poiché il prodotto con la sua trasposta da la matrice unità
![]()
Sia Li un sottospazio di Rn, l’insieme dei vettori di Rn ortogonale a Li è il complemento ortogonale di Li e viene indicato simbolicamente con Li┴.
Siano Ui=(u1,u2,..,ui) e U2=(uì+1,uì+2,..,un) due basi ortonormali, rispettivamente, di Li e Li┴ , allora ogni vettore rÎRn può essere scritto sotto forma di una somma di vettori
![]() con r1ÎLi e r2Î Li┴
con r1ÎLi e r2Î Li┴
gli addendi r1 e r2 rappresentano, rispettivamente, le proiezioni ortogonali del vettore r sui sottospazi Li e Li┴.
Dalla proprietà degli spazi lineari si ha che la proiezione ortogonale di una somma di vettori su un sottospazio è uguale alla somma delle proiezioni degli addendi.
Se si considera lo spazio ordinario R3 si ha che i suoi sottospazi propri hanno dimensione 1 e 2 , per cui è possibile avere le proiezioni ortogonali su rette e piani.
Esercizio 1.7: Sia U=(u1,u2,u3) un sistema ortonormale di coordinate di R3. Dimostrare che il sistema di vettori
![]()
rappresenta anche un sistema ortonormale di coordinate di R3 e la matrice di trasformazione è ortogonale. Se r=(2,3,1) sono le coordinate di r rispetto a U, calcolare le coordinate di r rispetto V.
1.7.2 Proiezione ortogonale ed obliqua di punti su un piano
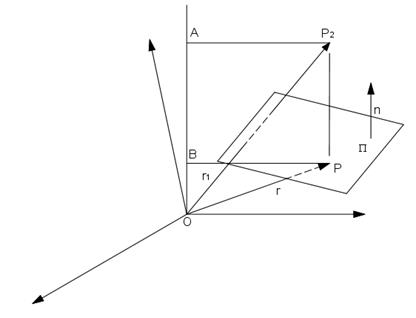
La formulazione vettoriale permette di calcolare facilmente la proiezione ortogonale di punti su un piano o su una retta. Sia P2 un generico punto e sia P la sua proiezione ortogonale su un piano Õ (r.n=p) (Fig. 1.11). Sommando i vettori posizione dei punti si ha
r= r2- |PP2| n
Considerando i prodotti scalari 0A=r2.n e 0B=p=r.n , è possibile calcolare la distanza |PP2| del punto P2 dal piano, che risulta essere data da
|PP2| =0A-0B= r2.n-r.n= r2.n -p
per cui la proiezione ortogonale del punto P2 sul piano di proiezione r.n=p è data da
r= r2- (r2.n -p) n (1.36)
Se il piano di proiezione coincide con un piano principale si ha p=0 e il versore n avrà due componenti nulle, pertanto come è ben evidente due coordinate del punto proiezione restano inalterate mentre la restante sarà uguale a zero. Ad esempio se il piano di proiezione coincide col piano principale xz ( n=(0,1,0) ) , dalla (1.36 ) si ha che la proiezione ortogonale di un generico punto r2=(x,y,z) è data da r=(x,0,z).
Quando l'equazione del piano è dato nella formulazione implicita f(x,y,z)=ax+by+cz+d=0 , per le relazioni esistenti tra coefficienti dell'equazione e versore normale al piano, si ha che la distanza del punto P2=(x2,y2,z2) può essere espressa anche da
![]() (1.37)
(1.37)
[Nota storica: Lagrange fu il primo a esprimere la distanza di un punto da un piano mediante la precedente formula.]
Fig. 1.11 : Proiezione ortogonale di un punto su un piano.
Applicando ad ogni vertice di un poliedro la (1.35) si otterrà la sua proiezione ortogonale su un assegnato piano Õ.
Se i punti appartengono ad un insieme continuo, che possono essere rappresentati da una curva parametrica r2(t), la (1.36) permette di calcolare la sua proiezione che è la curva parametrica r(t).
Consideriamo, come esempio, la proiezione di una retta passante per r2 ed avente per direzione u, la cui equazione è data da
![]()
Sostituendo la precedente equazione nella (1.36) abbiamo
![]()
che è l’equazione di una retta passante per la proiezione di r2 ed avente direzione u’=u-(u.n)n.
Il vettore u’ non è un versore, per calcolare il suo modulo è opportuno considerare che esso è normale ad n, per cui
![]()
Si osserva che se la retta è parallela al piano la sua proiezione conserva la direzione perché il prodotto scalare u.n=0.
Mentre se consideriamo la proiezione di due rette aventi direzione u1 ed u2, per confrontare le inclinazioni tra le rette e le loro proiezioni è necessario considerare i prodotti scalari
![]()
Esplicitando i prodotti scalari si ha una relazione tra gli angoli
![]()
Si osserva che in generale i due angoli non sono uguali, per cui l’inclinazioni tra rette nella proiezione non si conserva a meno che le due direzioni non siano parallele al piano di proiezione o sono parallele tra di loro. Nel primo caso i prodotti scalari sono uguali a zero per cui si ha cos( α’)=cos (α) mentre nel secondo caso essendo cos(α)=1 e u1=u2 la precedente relazione comporta che deve essere anche cos( α’)=1. Un altro caso in cui si conserva l’inclinazione tra le rette è quando sono tra di loro perpendicolari ed una è parallela al piano di proiezione. Infatti se si assume u1 normale ad n si ha
![]()
la precedente relazione è soddisfatta se cos( α’)=0, oppure se la retta u2 è parallela ad n ma quest’ultima condizione non permette di determinare cos( α’).
Problema 1.7: Determinare l’angolo tra la retta passanti per P1=(1,1,1) ed avente direzione parallela all’asse y con quella passante per P2=(1,2,1) ed avente direzione U2=(2,1,2). Calcolare, inoltre, l’equazioni delle proiezioni delle due rette sul piano xy e la loro inclinazione.
Soluzione : La retta 1 ha la direzione u1=(0,1,0), mentre la retta 2 ha come direzione il versore u2=(2/3,1/3,2/3). Il piano di proiezione ha normale n=(0,1,0) ed equazione r.n=y=0. Le equazioni delle due rette e le sue proiezioni sono
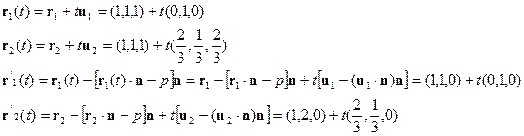
La direzione della proiezione della retta 2 è un vettore il cui modulo è sqrt(5)/3. L’angolo tra le due rette non è altro che l’arco coseno del prodotto scalare tra i versori, per cui
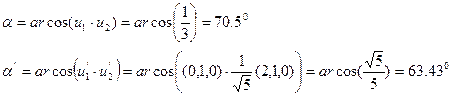
L'equazione (1.36) può essere ottenuta considerando la proiezione come un problema di intersezione tra una retta ed un piano, che è rappresentato dal seguente sistema di quattro equazioni nelle 4 incognite (x,y,z,t). Le prime tre equazioni sono l’equazione vettoriale della retta, mentre la quarta è l’equazione del piano di proiezione
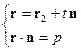
Sostituendo la prima equazione vettoriale nella seconda si ha
![]()
Sostituendo tale valore scalare nella equazione della retta si ottiene la (1.36).
Se consideriamo la proiezione obliqua occorre assegnare anche una direzione di proiezione l, per cui la retta di proiezione è data da r=r2+t l. Risolvendo il sistema precedente mediante il metodo di sostituzione si ha la proiezione obliqua di un punto su un piano
![]() (1.38)
(1.38)
1.7.3 Proiezione di un punto su una retta
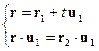
La determinazione della proiezione ortogonale del punto r2 su una retta passante per r1 e direzione u1 può essere ottenuta risolvendo il sistema di equazioni costituito dall'equazione vettoriale della retta e dall’equazione del piano passante per r2 e avente normale u1
Sostituendo la prima equazione nella seconda ed essendo u1 .u1=1 si ottiene il valore del parametro
t= (r2- r1). u1
che sostituito nella prima equazione permette di calcolare la proiezione ortogonale di r2 su una retta passante per r1 ed avente direzione u1
r= r1+ [(r2- r1). u1] u1 (1.39)
![]()
Per calcolare la distanza di un punto da una retta occorre calcolare il modulo del vettore ottenuto dalla differenza tra il vettore posizione del punto e la sua proiezione ortogonale. Utilizzando la (1.39) si ha
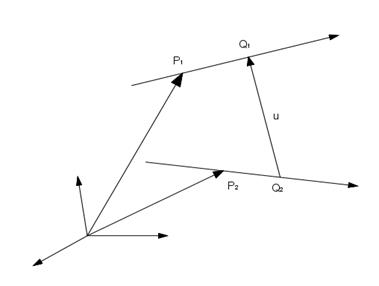
Il calcolo della distanza tra due rette sghembe può essere fatto considerando che esiste una perpendicolare comune passante per due punti appartenenti , rispettivamente , a ciascuna retta.
Se r= r1+tu1 e r= r2+tu2 sono le due rette e Q1 e Q2 sono i punti appartenenti alle due rette, che individuano la loro perpendicolare comune u, allora il segmento |Q2Q1| misura la loro distanza minima. Per calcolare tale distanza si consideri il vettore posizione del punto Q1 che è dato da
![]()
Moltiplicando scalarmente la precedente equazione per il vettore u , che è ortogonale a u1, u2 dove
![]()
si ottiene la distanza minima che è data da ![]()
Problema 1.8 : Calcolare la proiezione ortogonale del punto P2=(3,2,4) sul piano
passante per il punto P1=(1,1,1) e avente normale n=(1/3,2/3,2/3).
L’equazione del piano è data da (x,y,z).(1/3,2/3,2/3)=(1,1,1).(1/3,2/3,2/3)=2
Dalla (1.35) si ha
(x,y,z)=(3,2,4)-[(3,2,4).(1/3,2/3,2/3)-2] (1/3,2/3,2/3)=(3,2,4) -3 (1/3,2/3,2/3)= (2,0,2)
Problema 1.9 : Calcolare la distanza minima tra il punto r2 =(2,1,3) e la retta passante
per r1=(1,1,2) e direzione u=(1/3,2/3,2/3).
L’equazione della retta è r= r1+t u =(1,1,2)+t (1/3,2/3,2/3)
La distanza minima è data ha
![]()
Fig. 1.12 : Distanza minima tra due rette sghembe.
La proiezione ortogonale di un punto su una superficie può essere ottenuta dall’intersezione tra la superficie e la retta di proiezione passante per il punto e ortogonale alla superficie di proiezione. La distanza tra il punto e la sua proiezione rappresenta la distanza minima del punto dalla superficie. Una tale proiezione non rientra tra quelle previste nella classificazione delle proiezioni, perché pur essendo una proiezione ortogonale essa tuttavia non è una proiezione parallela perché la direzione della retta di proiezione dipende dal punto proiettato. Se la superficie è sferica il problema si semplifica abbastanza perché la retta di proiezione è data dalla congiungente il punto ed il centro della sfera.
Pertanto considereremo come superficie di proiezione una sfera.
Per semplicità supponiamo che la sfera di raggio R abbia il centro coincidente con l’origine degli assi cartesiani. Se P1=(x1,y1,z1) è un generico punto che si vuole proiettare, la sua proiezione si determina risolvendo il sistema di quattro equazioni costituite dalla retta di proiezione passante per P1 ed il centro della sfera e la superficie sferica
![]()
Sostituendo la prima equazione nella seconda si ottiene il valore del parametro t e da questo le tre coordinate del punto proiezione che sono date da
 (1.40)
(1.40)
Può essere interessante calcolare la proiezione per un insieme di punti e confrontare le proprietà geometriche delle due entità.
Se i punti appartengono ad una curva parametrica r1(t) , la sua proiezione è anche una curva parametrica che è data dalla (1.40) dove al posto della coordinate vanno considerate le corrispondenti funzioni parametriche x1(t), y1(t) e z1(t).
Per una generica curva è difficile analizzare le proprietà della sua proiezione su una superficie sferica, mentre può essere più facile se si considerano le proiezioni di rette situate in posizioni particolari.
Calcoliamo come primo esempio la proiezione di un segmento di retta aventi per estremi le coordinate P1=(0,R,0) e P2=(0,R,R). L’equazione che passa per i precedenti due punti è data da
![]()
che sostituita nella (1.40) al posto del generico punto P1 da
![]() (1.41)
(1.41)
E’ facile verificare che la curva (1.41) giace sul piano yz ed è un arco di circonferenza e rappresenta una formulazione parametrica razionale di un arco di circonferenza.
Come secondo esempio consideriamo la proiezione del segmento passante per i punti P1=(R,-R,R) e P2=(R,R,R), la cui equazione è data da
![]()
Dalla (1.40) si ottiene l’equazione della proiezione, che è data da
![]()
Si consideri un generico piano di proiezione che interseca gli assi principali nei punti P1=(x,0,0), P2=(0,y,0) e P3=(0,0,z). Si è visto in precedenza che se si proiettano su tale piano i versori principale si hanno dei rapporti di proiezione che dipendono dalle componenti del versore normale al piano di proiezione , che è dato da
![]()
Utilizzando le formule ottenute in precedenza si ottengono la distanza del piano dall'origine, che è data dal prodotto scalare tra il vettore posizione di uno dei tre punti assegnati ed n, e la proiezione O' dell'origine O del sistema cartesiano su tale piano
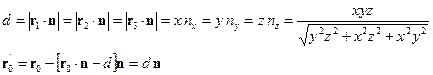 (1.42)
(1.42)
Le proiezioni dei versori principali individuano su tale piano un sistema di riferimento piano, che è utile quando si vuole disegnare una proiezione assonometrica dell’oggetto
Tale sistema piano è individuato dai vettori O'P1 = r1-r'o= (x-d nx,-d ny ,-d nz ), O'P2 = r2-r'o = (-d nx, y-d ny , -d nz ), e O'P3 = r3-r'o = (-d nx, -d ny , z-d nz ), i cui moduli sono uguali a
![]()
Per calcolare le inclinazioni tra i precedenti vettori, che indichiamo con α, β e γ , è sufficiente considerare i prodotti scalari tra i vettori
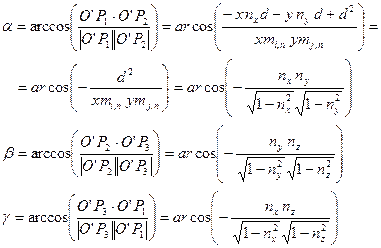 (1.43)
(1.43)
Una particolare proiezione assonometrica è quella isometrica, per tale proiezione il piano interseca gli assi principali ad una stessa distanza dall'origine per cui x=y=z. Sostituendo tali valori nella ( 1.42) si ha
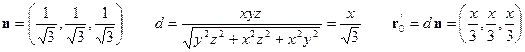
Sul piano isometrico i vettori O'P1 O'P2 e O'P3 sono uguali in modulo ed hanno le seguenti componenti
![]()
Sostituendo le componenti di n nella (1.41) si ha
![]()

La determinazione della proiezione prospettica di un arbitrario punto r1 richiede l’assegnazione del piano di proiezione e la posizione del punto di vista. Il calcolo della proiezione di r1 può essere ottenuto risolvendo il problema dell’intersezione tra la retta di proiezione passante per il punto di vista e r1 con il piano di proiezione, ottenendo così il seguente sistema di equazioni
dove r0 è il vettore posizione del punto di vista , n è la normale del piano di proiezione distante p dall’origine. Sostituendo la prima equazione nella seconda si ottiene il valore del parametro t
![]()
che sostituito nella prima equazione ci da le coordinate del punto proiezione
![]() (1.44)
(1.44)
dove d1 e d0 sono, rispettivamente, le distanze del punto r1 e del punto di vista r0 dal piano di proiezione, presi col segno algebrico, per cui se rispetto al piano di proiezione i due punti stanno su lati opposti le loro distanze hanno segni contrari.
Se consideriamo la proiezione di un vettore parallelo al piano di proiezione dato da a= r2 -r1, poiché d1 =d2 , dalla precedente equazione si ha
![]()
pertanto la direzione si conserva mentre il modulo del vettore proiezione può essere anche maggiore del modulo del vettore proiettato.
Esercizio: Calcolare la proiezione prospettica del punto r1=(3,2,1) sul piano di
proiezione passante per (1,1,1) e avente normale N=(1,1,1) e punto di vista
r0=(3,5,4).
Il piano di proiezione coincide con un piano della proiezione isometrica dove n=(1,1,1)/sqrt(3) ed è dato dal piano
![]()
Le distanze dal piano di proiezione di r1 e del punto di vista sono
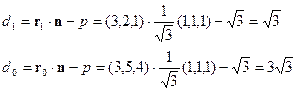
Sostituendo i valori calcolati nella (1.44) si ha
![]()
Capitolo II
2.1. Norme tecniche ed organismi normatori.
L’esigenza di definire delle norme tecniche si pose dopo la rivoluzione industriale per facilitare gli scambi di informazioni tecniche all’interno delle aziende industriali. Lo sviluppo industriale e l’espansione degli scambi commerciali imposero l’emanazione delle prime norme condivise da più aziende riguardanti sia le informazioni tecniche sia i prodotti.
All’inizio furono le aziende ad adottare delle norme interne che permettevano di risolvere problemi di comunicazione tra i suoi vari reparti, ma alla fine del 1800 si pose il problema di unificare le diverse norme aziendali, che spesso erano in contraddizione tra di loro, e si costituirono alcuni organismi normatori nazionali.
La presenza di enti normatori nazionali non limitò le aziende nell’emanazione di norme interne, soprattutto se queste non erano in contraddizione con le norme nazionali o coprivano dei settori in cui non vi erano delle norme nazionali, così anche oggi osserviamo che molte aziende adottano delle norme tecniche aziendali ( NTA).
La costituzioni degli tanti organismi nazionali, se da un lato favorì lo sviluppo industriale su scala nazionale, rappresentò anche un limite quando il commercio dei prodotti e lo scambio delle informazioni tecniche coinvolgevano più nazioni.
Dopo la seconda guerra mondiale, il mercato di molti prodotti era diventato internazionale, per cui si avvertì l’esigenza di costituire organismi normatori internazionali per l’emanazione di norme tecniche internazionali.Alcuni importanti enti di normazione nazionali sono:
ANSI |
American National Standard Institute |
AFNOR |
Association Francaise de Normalisation |
DIN |
Deutsche Industrie Normen |
UNI |
Ente Nazionale Italiano di Unificazione |
CEI |
Comitato Elettrotecnico Italiano |
BS |
British Standards |
Molte volte accanto agli enti nazionali esistono anche organizzazioni tecniche di categoria, associazioni industriali, ecc. che emanano specifiche o norme, come ASME ( American Society of Mechanical Engineers), IEEC ( Institute of Electrical and Electronic Engineers), UNAVIA ( Commissione Tecnica di Unificazione nell’Aeronautica), ATA ( Air Transport Association of America), AECMA ( European Association of Aerospace Industries), FAR ( Federal Aviation Regulation), FAA ( Federal Aviation Administration),ecc.. I principali enti normatori internazionali sono:
ISO |
International Standards Organization |
IEC |
International Electrotechnical Commission |
CEN |
European Committee for Standardization |
CENELEC |
Comitato Europeo per la Normazione Elettrotecnica |
Dal principio del secolo ad oggi, l’evoluzione della normazione non si è solo concretizzata in un allargamento di orizzonti geografici: la normazione ha infatti subito anche una sensibile evoluzione concettuale, che l’ha portata ad abbracciare significati sempre più ampi.
Oggi l’attività di normazione ha per oggetto anche la definizione dei processi, dei servizi e dei livelli di prestazione, intervenendo così in tutte le fasi di vita del prodotto, nelle attività di servizio e si occupa anche di definire gli aspetti di sicurezza, di organizzazione aziendale (UNI EN ISO 9000) e di protezione ambientale (UNI EN ISO 14000), così da tutelare le persone, le imprese e l’ambiente.
Secondo la Direttiva Europea 98/34/CE del 1998 si definisce come norma una specifica tecnica approvata da un organismo riconosciuto a svolgere attività normativa per applicazione ripetuta o continua, la cui osservanza non sia obbligatoria e che appartenga ad una delle seguenti categorie:
Le norme, quindi, sono documenti che definiscono le caratteristiche (dimensionali, di prestazioni, ambientali, di sicurezza, di organizzazione ecc.) di un prodotto, processo o servizio, secondo lo stato dell'arte. L’iter che porta alla nascita di una norma si articola in diverse fasi: la messa allo studio, la stesura del documento, l'inchiesta pubblica, l'approvazione da parte della CCT e la pubblicazione. Le parti economico/sociali interessate possono prendere parte all'iter di elaborazione di una norma, partecipando ai lavori di Commissione o inviando all'ente di normazione i propri commenti.
La messa allo studio
Gli organi preposti dell'organismo di normazione elaborano uno studio di fattibilità che mette in relazione la situazione del mercato con le necessità normative, valutano le risorse e le competenze da coinvolgere, nonché i benefici. Se il risultato dell'analisi è positivo si procede alla stesura del progetto di norma.
La stesura del documento
L'organismo di normazione svolge una funzione di coordinamento dei lavori, mettendo a disposizione la propria struttura organizzativa, mentre i contenuti delle norme vengono definiti dagli esperti esterni che, in ambito europeo ed internazionale, vengono nominati dai singoli Paesi.
La discussione della bozza di norma, messa a punto tramite il lavoro a distanza su internet e/o per mezzo di apposite riunioni, ha come obiettivo l'approvazione consensuale della struttura e dei contenuti tecnici del progetto di norma.
L'inchiesta pubblica
Il progetto di norma approvato viene reso disponibile al mercato, mediante comunicazione sui canali d'informazione degli organismi di normazione (per una durata variabile in funzione della tipologia del documento) al fine di raccogliere commenti ed ottenere il più ampio consenso: tutte le parti economico/sociali interessate, in particolare coloro che non hanno potuto partecipare alla prima fase della discussione, possono così contribuire al processo normativo. Negli ambiti europei ed internazionali, tali commenti possono essere inoltrati al CEN e all'ISO soltanto tramite gli organismi di normazione nazionali.
La pubblicazione
La versione definitivamente concordata tiene conto delle osservazioni raccolte durante l'inchiesta pubblica. Nel caso di norme nazionali, il progetto finale viene esaminato dalla Commissione Centrale Tecnica per approvazione, mentre a livello europeo ed internazionale, viene sottoposto al voto degli organismi di normazione nazionali al fine di essere ratificato e pubblicato come norma.
A livello europeo ogni membro CEN ha l'obbligo di recepire le norme EN (che diventano UNI EN in Italia) eventualmente pubblicandole nella propria lingua, e ritirando quelle nazionali esistenti sul medesimo argomento. Tale obbligo non esiste invece per le norme ISO che possono essere volontariamente adottate (con la sigla UNI ISO in Italia).
Qualsiasi norma tecnica deve avere le seguenti caratteristiche:
CONSENSUALITÀ: deve essere approvata con il consenso di coloro che hanno partecipato ai lavori.
DEMOCRATICITÀ: tutte le parti economico/sociali interessate possono partecipare ai lavori e, soprattutto, chiunque è messo in grado di formulare osservazioni nell'iter che precede l'approvazione finale.
TRASPARENZA: UNI segnala le tappe fondamentali dell'iter di approvazione di un progetto di norma, tenendo il progetto stesso a disposizione degli interessati.
VOLONTARIETÀ: le norme sono un riferimento che le parti interessate si impongono spontaneamente.
2.1.2. Introduzione alla ICS
Ogni norma è individuata dalla sigla dell’ente di normazione e da un numero, che viene assegnato in modo progressivo, per cui diventa difficile la ricerca delle norme riguardanti un particolare settore.
Per facilitare la ricerca delle norme, l’ISO adottò un sistema di classificazione per le Norme Tecniche denominato ICS (International Classification for Standards). Dal 1997 tutte le norme ISO oltre al numero contengono sulla prima pagine la classificazione ICS, ciò ha permesso di fornire un criterio univoco e razionale alla struttura di cataloghi e repertori di norme tecniche. Tale classificazione é stato favorevolmente accolto dalla maggioranza dei membri ISO ed è stata adottata da alcuni di loro.
L'UNI, in qualità di membro dell'ISO, già dall' edizione 1993 del suo catalogo ha sostituito il vecchio criterio di classificazione, basato sulla CDU (Classificazione Decimale Universale) ormai ritenuta obsoleta da quasi tutti gli Enti normatori, con la ICS. Il sistema di classificazioni ICS si articola sulla base di un ordinamento gerarchico consistente di tre livelli numericamente rappresentati e separati tra di loro da un punto.
Costituito dalle prime due cifre, definisce 41 campi di applicazione, denominati "campi fondamentali", in cui le norme possono trovare applicazione.
Esempio:
43 - Tecnica dei Veicoli Stradali
17 – Metrologia e misurazioni
21 – Sistemi e componenti meccanici per uso generale
Si compone di complessivi 358 gruppi, rappresentati da tre cifre precedute da quelle del campo fondamentale sopra descritto.
Esempio:
21 - Sistemi e componenti meccanici per uso generale
21.060 – Elementi di collegamento
É un'ulteriore esplosione dei 358 gruppi di cui sopra. Viene rappresentato dalla ultime due cifre.
Esempio:
21 - Sistemi e componenti meccanici per uso generale
21.060 – Elementi di collegamento
21-060.10 -Viti, viti prigioniere e tiranti
Le norme così classificate sono proposte in tutti i campi nei quali possono trovare applicazione. Per esempio, la norma "UNI 9940 - Gruppi di sicurezza idraulica per riscaldatori ad accumulo - Requisiti e prove" è rintracciabile nel presente catalogo nei due punti seguenti:
13.120 Sicurezza domestica e
91.140.70 Apparecchi Sanitari
Ad ogni Organismo normatore nazionale è lasciata facoltà di introdurre un ulteriore livello laddove sia giustificato dalla presenza di numerose norme di diversa tipologia in un medesimo gruppo o sottogruppo. Questo ulteriore sotto-sottogruppo è costituito da due cifre precedute da un trattino.
L'ambito dinamico della normazione, in continua evoluzione col progredire della tecnica, può rendere l'ICS soggetto ad aggiornamenti, da parte dell'ISO, per cui l'attuale classificazione è senz'altro destinata ad arricchirsi e a perfezionarsi nel corso del tempo.
Viene mostrata la prima pagina della norma UNI EN ISO 5456 emanata nel febbraio del 2001 che definisce i metodi di proiezione.
La presenza delle sigle UNI EN ISO, indica che è una norma nazionale, europea ed internazionale. La classificazione ICS è 01.100.01
2.2 Metodi di disposizione delle proiezioni
Il Disegno Tecnico utilizza principalmente le proiezioni ortografiche per rappresentare degli oggetti e solo raramente per scopi puramente di presentazione commerciale di un prodotto si possono utilizzare le proiezioni assonometriche o prospettiche.
La più recente Norma che illustra i vari metodi di proiezione è la UNI EN ISO 5456 del 2001 ( ICS 01.100.01). La norma ISO 5456 è costituita da 4 parte, nella prima parte (5456-1) vi è una panoramica dei metodi di proiezione, nella parte 5456-2 sono descritte le proiezioni ortografiche e i metodi di disposizione delle proiezioni o viste, nella parte 5456-3 sono descritte le proiezioni assonometriche, infine nella quarta parte (5456-4) sono descritte le proiezioni prospettiche.
Le sei proiezioni ortografiche di un oggetto sono individuate da una direzione a cui viene assegnata una lettera minuscola dell’alfabeto, mentre la corrispondente vista è indicata dalla lettera maiuscola.
La vista maggiormente rappresentativa dell’oggetto viene scelta come vista principale e rappresenta la vista frontale. Le sei viste sono così designate:
Vista in direzione |
Vista |
Designazione della vista |
a |
frontale |
A |
b |
dall’alto |
B |
c |
da sinistra |
C |
d |
da destra |
D |
e |
dal basso |
E |
f |
posteriore |
F |
Rispetto alla vista A occorre ruotare le altre viste in modo da avere su un unico foglio di disegno tutte le altre viste. La Norma ISO 5456 prevede quattro metodi di disposizione delle viste che vengono indicati come : primo diedro, terzo diedro, frecce di riferimento, rappresentazione ortografica speculare.
Nel metodo del I diedro ( spesso indicato come metodo europeo) l’oggetto è situato tra l’osservatore ed i piani di proiezione, le posizioni delle viste rispetto alla vista A sono determinate dalla rotazione dei piani di proiezione attorno a linee coincidenti o parallele agli assi principali del sistema di riferimento in modo da avere la vista sullo stesso piano su cui è riportata la vista A, ovviamente la vista ruotata non deve sovrapporsi alla vista A. Pertanto, con il metodo del I Diedro, le viste sono disposte rispetto alla vista principale A nel modo seguente:
Il segno grafico che identifica questo metodo, che va sempre posto nel cartiglio, è anche riportato nella Figura 2.1.
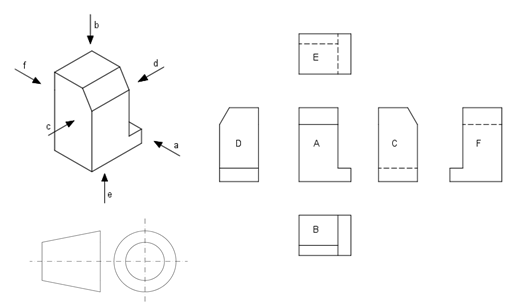

Figura. 2.1 : Metodo I diedro
Nel metodo del Terzo Diedro ( metodo americano) il piano di proiezione è disposto tra l’oggetto e l’osservatore e le posizioni delle varie viste rispetto alla vista principale A sono determinate dalla rotazione dei piani di proiezione, che sono coincidenti o paralleli ai piani principali, in modo da avere sullo stesso piano della Vista A le altre viste.
La disposizione delle viste col metodo del III diedro e il relativo simbolo sono riportate nelle seguente Figura 2.2.
Nei casi in cui si preferisce posizionare liberamente le viste rispetto alla vista principale si deve utilizzare il metodo delle frecce di riferimento. Con tale metodo,sulla vista principale viene riportata una freccia a cui è associata una lettera maiuscola, che indica la direzione di proiezione della vista. Le viste così identificate possono essere disposte liberamente sul foglio di disegno e nessun simbolo grafico è previsto per identificate questo metodo.
Il metodo delle frecce di riferimento è particolarmente utile se una faccia dell’oggetto non è parallela a nessun piano principale, per cui alcune entità geometriche appartenenti alla faccia presentano rapporti di proiezione differenti da uno se sono proiettate sui piani principali. Il metodo delle frecce di riferimento può essere utilizzato in aggiunta agli altri due metodi.
Nei disegni di costruzione può essere utilizzato il metodo della rappresentazione ortografica speculare, in cui la vista dell’oggetto è una riproduzione dell’immagine in uno specchio disposto, di norma, parallelamente ad un piano dell’oggetto. La vista ottenuta tale metodo deve contenere la traccia del piano dello specchio e una lettera maiuscola per l’indicazione della vista.
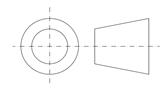
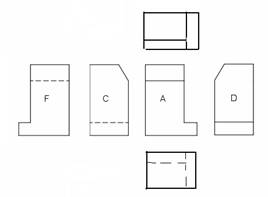
Figura 2.2 : Metodo III Diedro
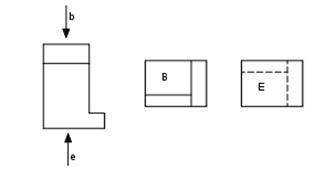
Figura 2.3 : Metodo delle frecce di riferimento
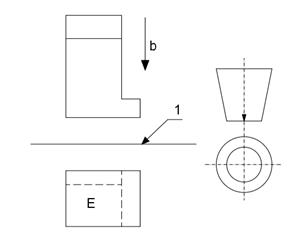
Figura 2.4 Metodo rappresentazione ortografica speculare
2.3 Formato dei fogli, riquadro delle iscrizioni, ecc.
I disegni dovrebbero essere eseguiti su fogli di dimensioni minime compatibili con la necessaria chiarezza richiesta per poter analizzare e leggere la rappresentazione grafica dell’oggetto. I fogli sono disponibili in formati della serie principale ISO-A (UNI EN ISO 5457), dove il formato A0 ha una forma rettangolare avente superficie uguale ad 1 m2 e il rapporto tra i lati uguali a sqrt(2). Se si divide il formato A0 secondo il lato maggiore si ottiene il formato A1 dove il rapporto tra i lati è uguale a quello di A0. Analogamente è possibile definire formati più piccoli.
I formati più grandi vengono indicati con 2A0, 3A0, ecc. e si ottengono raddoppiando, triplicando, ecc. la lunghezza dal formato A0. Per esigenza di riproduzione i grandi formati nA0 hanno una lunghezza che non è esattamente uguale a n volte la lunghezza del formato A0, perché è previsto uno spazio di sovrapposizione di larghezza uguale a 148.5 mm. Pertanto le larghezze dei formati 2A0, 3A0 sono rispettivamente uguali a L=2x1189-148.5=2229.5 e L=3x1189-2x148.5=3270.
La designazione del formato dei fogli deve essere collocata sul bordo dell’angolo inferiore destro del foglio. Tutti i formati devono prevedere dei margini contenuti entro i bordi del foglio rifiliato. Sul bordo sinistro la larghezza del margine è di 20 mm mentre per gli altri bordi la larghezza dei margini è di 10 mm.
Per facilitare la riproduzione del disegno si devono prevedere quattro segni di centratura che sono posizionati all’estremità dei due assi di simmetria del foglio rifilato.
I fogli devono presentare un sistema di riferimento lungo i margini del foglio al fine di consentire l’immediata individuazione di particolari aree del disegno. Generalmente, i riferimenti verticali sono contrassegnati da lettere maiuscole ( non si utilizzano le lettere I e O), mentre i riferimenti orizzontali sono dei numeri. Le larghezze delle divisioni in cui si collocano i riferimenti sono di 50 mm a partire dagli assi di simmetria del formato rifilato. Per il formato A4 i riferimenti sono collocati solo sul lato destro del foglio.
Formato dei fogli rifilati e non e zona esecuzione disegno |
||||||
Designazione |
Dim. Foglio rifilato |
Zona disegno |
Foglio non rifilato |
|||
A0 |
841 |
1189 |
821 |
1159 |
880 |
1230 |
A1 |
594 |
841 |
574 |
811 |
625 |
880 |
A2 |
420 |
594 |
400 |
564 |
450 |
625 |
A3 |
297 |
420 |
277 |
390 |
330 |
450 |
A4 |
210 |
297 |
180 |
277 |
240 |
330 |
I fogli devono presentare un sistema di riferimento lungo i margini del foglio al fine di consentire l’immediata individuazione di particolari aree del disegno. Generalmente, i riferimenti verticali sono contrassegnati da lettere maiuscole ( non si utilizzano le lettere I e O), mentre i riferimenti orizzontali sono dei numeri. Le larghezze delle divisioni in cui si collocano i riferimenti sono di 50 mm a partire dagli assi di simmetria del formato rifilato. Per il formato A4 i riferimenti sono collocati solo sul lato destro del foglio.
Il foglio deve contenere sia il disegno sia il riquadro delle iscrizioni ( cartiglio), la cui collocazione per i formati da A1 ad A3 è in corrispondenza dell’angolo inferiore destro della zona di disegno, questi formati devono essere posizionati orizzontalmente. Per il formato A4, che va posizionato verticalmente, il riquadro delle iscrizioni è situato lungo il lato corto della zona per il disegno.
Il riquadro delle iscrizioni ( UNI 8187, ISO 7200) contiene informazioni relative alla identificazione, interpretazione e gestione del disegno. La forma del riquadro delle iscrizioni è rettangolare e viene suddiviso in tante caselle le cui dimensioni non sono vincolate dalla norma ma dipendono dalle specifiche informazioni inscritte. Alcune informazioni sono presenti sempre come l’identificazione dell’Azienda, l’oggetto, il disegnatore, data, la Scala, il simbolo del metodo di disposizione delle viste, ecc..
Le dimensioni del riquadro delle iscrizioni sono conseguenza della sua posizione sul formato A4, pertanto esso ha una larghezza di 190 mm ( per fogli con margine sinistro di 10 mm) o di 175 mm ( per fogli con margine sinistro di 25 mm), mentre la sua altezza non deve superare 148.5 mm che è la metà dell’altezza del formato A4.
Nell’ambito di una stessa azienda, il riquadro delle iscrizioni deve avere un’identica configurazione per i diversi formati.
Nelle aziende con una organizzazione semplice, per contenere la quantità di documenti in circolazione, è preferibile riportare nel riquadro anche una telegrafica descrizione degli aggiornamenti. Se lo spazio del riquadro non è sufficiente a contenere le informazioni può espandersi verso l’alto, come nel caso di un disegno di complessivo di un prodotto assemblato per cui occorre riportare nel riquadro anche una sommaria descrizione riguardanti tutte le componenti o parti del prodotto.
Per identificare le parti vengono riportate nel disegno complessivo delle linee di richiamo (UNI EN ISO 6433-97) con dei numero di posizione per ogni parte. Se i numeri di posizione sono inscritti in una circonferenza, le linee di richiamo devono essere dirette verso il centro della parte. In Fig. 2.1 sono mostrati esempi di linee di richiamo.
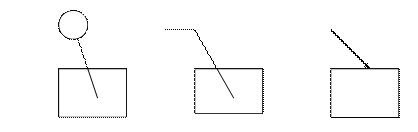

Fig. 2.4 Linee di richiamo e numeri di posizione
Per una migliore leggibilità del disegno è preferibile disporre i numeri di posizione secondo linee orizzontali o verticali. L’assegnazione dei numeri di posizione deve rispettare un ordine che può dipendere:
Nel cartiglio ogni componente è identificata dal numero di posizione e spesso anche da un Part/Number, che è un codice assegnato dall’azienda a quel particolare componente.
Il riquadro delle iscrizioni è solo una parte del disegno che contiene informazioni scritte, altre informazioni sono contenute in documenti allegati ai disegni complessivi o di dettaglio come la Distinta Componenti ( UNI ISO 7573), che è l’elenco completo di tutti i componenti del prodotto. La corrispondenza tra gli elementi di una distinta componenti e la loro rappresentazione sul corrispondente disegno viene espletata dai numeri di posizione o dal Part/Number.
E’ possibile compilare diverse distinte per scopi differenti come il rilevamento dei tempi, la gestione delle scorte, ecc..
La Distinta Componenti, spesso denominata “Lista Dettaglio”, può non essere compilata per prodotti semplici, se è possibile inserire tutte le informazioni nel Riquadro delle Iscrizioni. Viceversa, se esiste una Distinta Componenti essa deve essere identificata dallo stesso codice del relativo disegno e per poterla meglio distinguere da altri documenti, la norma raccomanda che il codice sia preceduto dal prefisso “distinta”.
La Distinta Componenti è strutturata in più colonne in cui vengono riportate le informazioni sotto le intestazioni seguenti:
Nella colonna “individuazione” si riporta il numero di posizione o codice della parte come indicato sul disegno.
La colonna “descrizione” riporta il nome della parte o una sua sommaria descrizione. Nel caso di parti normalizzate ( per esempio viti, chiodi, ecc.) la loro designazione deve essere conforme a quella prevista dalle norme specifiche.
Nella colonna “quantità” si indica, per ciascuno componente, il numero totale degli elementi utilizzati per la costruzione del prodotto rappresentato nel disegno complessivo.
La colonna “riferimenti” viene utilizzata per richiamare componenti che non vengono completamente rappresentati sul disegno, come le parti rappresentati in altri disegni, normalizzati, ecc..
La colonna “materiali” riporta il tipo e la qualità di materiale utilizzato e se esso è normalizzato occorre indicare la sua designazione normalizzata.
La distinta componenti può contenere altre informazioni necessarie per il prodotto finito come: codice di magazzino, massa unitaria, stato di fornitura, note.
La sequenza delle iscrizioni sulla distinta deve essere la stessa usata dai numeri di posizione apposti sul disegno complessivo. Se la distinta componenti è indicata sul disegno ( cartiglio) la sequenza deve essere dal basso verso l’alto, con le intestazione delle colonne alla base.
Spesso nell’angolo superiore destro del foglio è riportata la Colonna Modifiche in cui si indicano la descrizione della revisione del disegno, con data e firma di chi l’ha approvata.
Su molti fogli di disegni aerospaziali vi sono delle caselle complementari come:
5 |
|
|
Smussi non quotati |
Rugosità |
||||
4 |
|
|
||||||
3 |
|
|
Trattamento termico |
|||||
2 |
|
|
||||||
1 |
|
|
N. Modello |
|||||
N |
Descrizione |
Quant. |
Data |
|||||
Disegnatore |
Controllore |
Quote senza indicazione di tolleranza |
Scala |
Simbolo |
||||
DITTA |
Titolo del disegno |
|||||||
Fonte: https://www.docenti.unina.it/downloadPub.do?tipoFile=md&id=131355
Sito web da visitare: https://www.docenti.unina.it/
Autore del testo: E. Santoro -Appunti sulle Proiezioni
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve