Elettricità

 

 

 

I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore

 

 

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

 

 

 

Elettricità

L’elettricità                                      

La materia è costituita essenzialmente da atomi che a loro volta sono costituiti da protoni, neutroni ed elettroni, mentre gli elettroni, più leggeri, ruotano attorno al nucleo.
Si può comunque dire che alcuni corpi, a causa della loro struttura atomica, possiedono elettroni che sono debolmente vincolati ai rispettivi nuclei atomici e sono detti “elettroni liberi”, i quali opportunamente stimolati  (vedi ad Es. una pila), si spostano da un polo all’altro  in modo ordinato.           
Parliamo dunque della corrente elettrica.
Come dice la parola stessa, corrente e' qualcosa che scorre, che fluisce all'interno di alcuni materiali; si definisce quindi corrente elettrica (elettricità) il movimento (o flusso) ordinato degli elettroni che si spostano da un polo all’altro. Tali materiali, proprio perché si prestano a consentire questo flusso, vengono definiti conduttori. Altri materiali, che invece si oppongono al passaggio della corrente, vengono definiti isolanti ( in questi materiali gli elettroni sono forte- mente attratti dal nucleo centrale dell’atomo).
I materiali conduttori che più ci interessano sono i metalli (ad esempio il rame, l'argento e l'alluminio, che vengono usati per costruire i cavi elettrici).
Tra i materiali isolanti ricordiamo il vetro, il marmo, la plastica, la gomma, il sughero, il legno e la carta (se sono ben asciutti)
Le grandezze elettriche prese in esame in questo grande fenomeno  sono tre :

• Tensione
• Resistenza
• Intensità

  
     Tensione o Potenziale
Perché ci sia corrente elettrica, deve esistere una differenza di potenziale agli estremi del conduttore e quindi un campo di forze elettrico(es. Pila)
In particolare, un generatore di tensione  ha due morsetti: il polo positivo, con potenziale elettrico più elevato (abbiamo una mancanza di elettroni), ed il polo negativo (abbiamo un eccesso di elettroni) con potenziale elettrico minore.
Il passaggio di elettroni tende a livellare il potenziale tra i due poli.
Similitudine idraulica

Il circuito in questione si dice chiuso perché l'acqua aspirata ritorna al serbatoio attraverso la pompa per poi ritornare in circolo.
In un circuito elettrico  il flusso di elettroni è continuo  fin quando esiste la differenza di potenziale  tra i due poli e più precisamente fin quando la sostanza acida presente nel generatore  stimola il Polo Positivo a perdere elettroni e quello Negativo ad acquistare elettroni.
Occorre però fare una precisazione: negli impianti elettrici di casa nostra non c'e' la corrente, ma c'e' la tensione, ovvero quella forza che spinge gli elettroni a muoversi, dando origine alla corrente. Questa forza ha un valore ben preciso, che si indica con un numero, abbinato ad una unità di misura:  il volt,possiamo dire che la tensione disponibile  nelle prese di casa nostra misura 220 volt.
Resistenza  elettrica
Abbiamo visto che la corrente scorre per effetto di una forza detta forza elettromotrice o tensione; c'è però qualcosa che contrasta di più o di meno questa forza e tende a frenare lo scorrere degli elettroni: questa forza frenante, che dipende dalla natura del materiale attraversato, viene detta resistenza elettrica.
L’intensità luminosa che avremo in un semplice circuito elettrico dipenderà da alcuni fattori:

• dalla forza elettromotrice, o tensione, applicata
•  dalla resistenza del materiale

 quest’ultimi  strettamente legati alle leggi  di Ohm Georg Simon( fisico tedesco) e descritte dalle seguenti  relazioni matematiche.
Prima Legge di Ohm: Resistenza Elettrica
Prima Legge di Ohm: Il rapporto tra la d.d.p. V tra due punti di un conduttore metallico a temperatura costante e l’intensità di corrente che fluisce in esso è costante. La resistenza determina l'intensità della corrente che fluisce attraverso il circuito, ai cui capi è applicata una differenza di potenziale.

•        dove si evince che il valore della Resistenza è inversamente proporzionale a quello dell’Intensità luminosa (I =V/R), mantenendo costante il valore della tensione applicata.

Si consideri che il valore  dell’intensità della corrente elettrica  corrisponde alla quantità di cariche elettriche che passano in un determinato punto del circuito ed anche in un particolare momento.

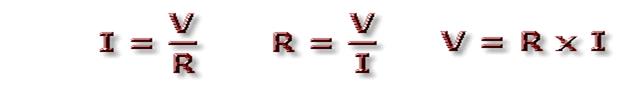
Seconda Legge di Ohm: Resistività
Seconda legge di Ohm: A parità di ogni altra condizione, la resistenza R di un conduttore è direttamente proporzionale alla sua lunghezza e inversamente proporzionale alla sua sezione (u.m. Ωmm2/m)   Resistività è la misura della capacità del materiale di opporsi al fluire in esso della corrente elettrica (indipendentemente dalle sue dimensioni e dalla sua forma, Campione di lunghezza e sezione unitarie)
Filo utilizzato in elettricità
 Più grande è la lunghezza del filo più grande è la resistenza R
Più piccola è la lunghezza del filo più piccola è la resistenza R
                                         Più grande è lo spessore del filo più piccola è la resistenza R
Più piccolo è lo spessore del filo più grande è la resistenza R

•   seconda legge di Ohm, che permette di calcolare la resistenza di un mate riale a partire dalle sue caratteristiche fisiche e geometriche (spessore , lunghezza)

dove  è la resistività del materiale (anche detta resistenza elettrica specifica, è l'attitudine di un materiale a opporre resistenza al passaggio delle cariche elettriche. Nel sistema internazionale la resistività si misura in ohm per metro (Ω·m).
 Conduttori
I materiali  sono catalogati a seconda della maggiore o minore capacità di far passare gli elettroni al loro interno.
Appartengono al primo gruppo tutti i metalli, come, ad esempio, rame (Cu), argento (Ag), Alluminio (Al).
Isolanti
In un isolante non esistono elettroni di valenza liberi di muoversi e tali da evidenziare un flusso di cariche ordinate, sotto l’azione di un campo elettrico. In realtà non esistono isolanti perfetti, ma sostanze definite isolanti perché offrono una resistenza assai grande al passaggio di cariche elettriche.
l è la lunghezza del filo, misurata in metri
S è l'area della sezione, misurata in metri2

Passiamo ad analizzare più  da vicino il comportamento  degli impianti  elettrici che più di altri  passano sotto i nostri occhi.
Il circuito elettrico è costituito :
      

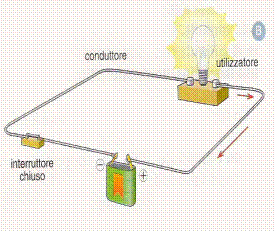
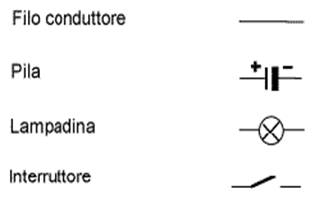
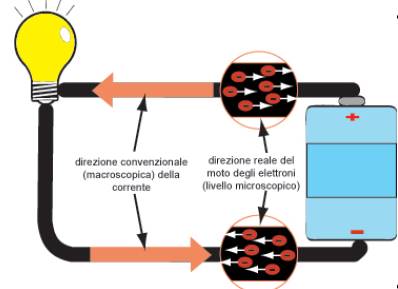
Il verso della corrente
Gli impianti elettrici più comuni:

Circuito elettrico in serie di più generatori  (in questo caso avremo  una tensione di   4,5V x 3= 13,5 Volt)

                                   
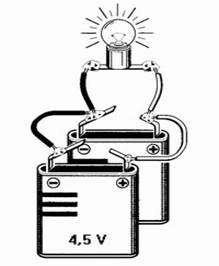
Circuito elettrico in parallelo di più generatori                     Circuito elettrico in serie di più utilizzatori (lampadine),
 (in questo caso avremo  una tensione   paria 4,5 Volt)       ogni lampadina avrà una tensione pari a  1/3  di 4,5 V 

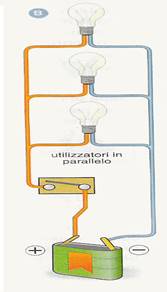
 Circuito elettrico in parallelo di più lampadine

Analizziamo   alcuni   circuiti  in “Serie”
Se "n" resistenze sono collegate in serie, la resistenza totale è la somma delle singole resistenze
R = R1 + R2 + .... + Rn
      
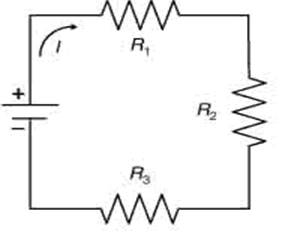
Esempio di Resistenza in serie                          Esempio di utilizzatori in serie
Collegamento in serie: tutti gli utilizzatori sono attraversati dalla stessa corrente; la tensione si ripartisce sui vari utilizzatori.
Esempio caratteristico di collegamento in serie sono le lampadine dell'albero di natale, la tensione di 220 volt della presa di casa nostra risulta applicata a tutta la fila di lampadine  (10 lampadine tutte aventi le stesse caratteristiche elettriche), quindi per far passare corrente deve vincere la resistenza non di una sola, ma di tutte le lampadine, una dopo l'altra; la resistenza che incontra la tensione è equivalente quindi alla somma di tutte le resistenze. La tensione di 220 volt si suddividerà allora tra le varie lampadine, e su ogni lampadina sarà presente la tensione che occorre perché la corrente in circuito possa superare la resistenza di quella lampadina. Se supponiamo di collegare in fila 10 lampadine identiche, troveremo che su ogni lampada sarà presente una tensione di 22 volt. Se una di esse venisse collegata da sola alla rete a 220 volt, scoppierebbe immediatamente; insieme alle altre invece essa sopporta solo una piccola parte della tensione di rete e può funzionare senza bruciarsi.

01 - Resistori in serie.
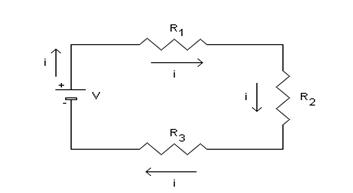
Consideriamo il seguente circuito :

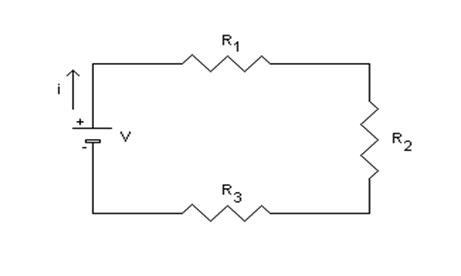
        (si noti il verso convenzionale della corrente dal  +  al - )
Si tratta di un circuito che presenta tre resistori collegati in serie, di resistenza  , , rispettivamente.

Se poniamo  :
        ,
chiamando 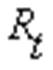   resistenza totale, avremo :
  .
Questa formula è identica a quella di un circuito con un solo resistore !!!
Il circuito in questione è quindi equivalente al seguente circuito dotato di un unico resistore con resistenza uguale alla somma delle tre resistenze originali :

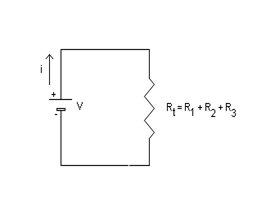
E' importante infine riassumere ciò che caratterizza un circuito di resistori collegati in serie :

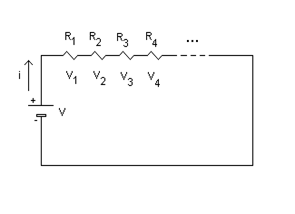
 - 1 -    nei singoli resistori e nel generatore stesso circola la medesima corrente    
        - 2 -    la somma delle tensioni del generatore, cioè :
                            ,
        - 3 -    la resistenza equivalente (totale) è data dalla somma delle resistenze cioè :
                            .
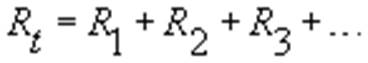Consideriamo i seguenti esempi :
        - 1 -    esempio 
Nel caso del circuito con tre resistenze in serie, si abbia :
        .
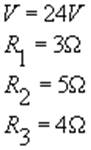Calcoliamo subito la resistenza totale :
        .
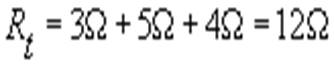Essendo 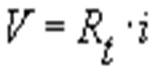 , si ricava la corrente :

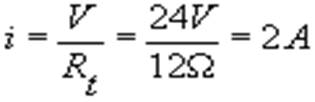
La corrente che circola in ciascun resistore e nel generatore stesso è quindi di due ampere.

• Se utilizziamo un numero inferiore di utilizzatori, avremmo  ai capi di ogni lampadina una maggiore potenza  con il rischio di bruciarle.
• Se utilizziamo un numero superiore di utilizzatori, avremmo che ai capi di ogni lampadina una minore potenza  con il rischio questo produrrebbe meno luce.
• Se una lampadina si fulmina, il circuito si interrompe e non passa più corrente.

Circuiti elettrici in parallelo
Volendo collegare alla rete diverse lampadine, la tensione sarà la stessa per tutti gli utilizzatori; ogni utilizzatore assorbe la sua corrente in tal modo ognuna delle lampade risulta collegata a 220 volt ed assorbe la corrente che il suo filamento lascia passare.

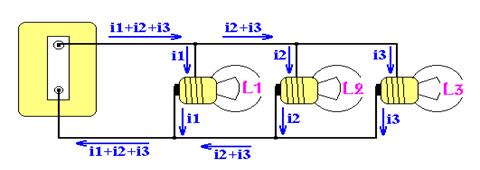
Con il collegamento in parallelo di "n" resistenze si sommano le conduttanze, rispettivamente i reciproci delle resistenze:

• Se utilizziamo un numero inferiore di utilizzatori, avremmo  ai capi di ogni lampadina una maggiore potenza  con il rischio di bruciarle.
• Se utilizziamo un numero superiore di utilizzatori, avremmo che ai capi di ogni lampadina una minore potenza  con il rischio questo produrrebbe meno luce.
• Se una lampadina si fulmina, il circuito si interrompe e non passa più corrente.
• - 2 -    esempio 

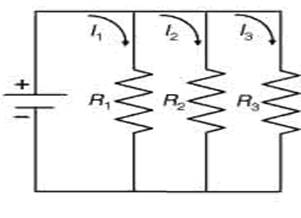
- Resistori in parallelo.
Consideriamo il seguente circuito elettrico :
         
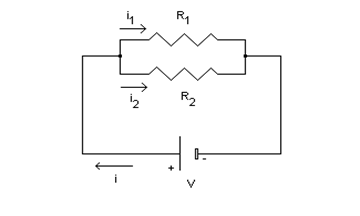
I due resistori di resistenza    ed    si dice che sono collegati in parallelo perché i loro estremi sono collegati assieme nei punti   e  .
Intuitivamente, è come se la corrente, entrando nei due resistori, si "dividesse" (in generale in parti diverse) e poi si "ricomponesse" uscendo da essi.
Le due correnti sono immediatamente calcolabili. Abbiamo :
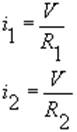           per cui :     
Vediamo il seguente esempio in cui abbiamo tre resistori in parallelo (ovviamente, le considerazioni fatte per due resistori in parallelo valgono anche per    resistori in parallelo).

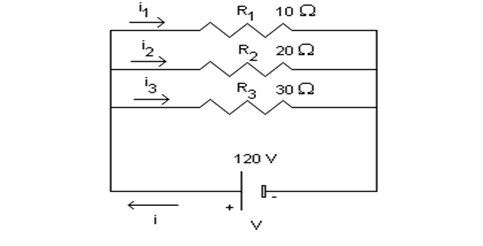
Le tre correnti sono date da :

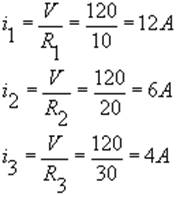
Si noti che si hanno correnti minori dove la resistenza è maggiore, come è giusto che sia.

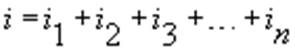
Diamo, senza dimostrazione, il valore della resistenza equivalente. Essa vale :

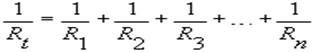
Nel caso di due resistori, la formula può essere scritta in un'unica frazione (facendo il minimo comune multiplo dei denominatori) :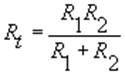
E' facile rendersi conto che la resistenza totale  , per i resistori in parallelo, è minore di ciascuna resistenza. Si ha cioè :
        .                                           
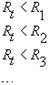Vediamolo matematicamente nel caso di due resistori in parallelo.
       
Fisicamente si capisce che aggiungendo un resistore in parallelo si ottiene una resistenza complessiva minore perché si aumenta la corrente totale a parità di tensione, essendo :
         
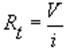
per cui, aumentando    diminuisce  , a parità di  .
Nel caso di due resistenze uguali (ciascuna di valore  ) in parallelo si ha :

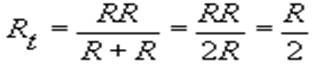
ovvero la resistenza totale è metà di una delle due come è giusto che sia.
Riassumiamo infine ciò che caratterizza un circuito di resistori collegati in parallelo :
       
        - 1 -    la somma delle correnti che circolano nei resistori eguaglia la corrente che circola nel generatore, cioè :
                           
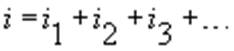
        - 2 -    ai capi dei resistori vi è la stessa tensione, quella del generatore
        - 3 -    la resistenza equivalente (totale) è data dalla formula :
                            .
      
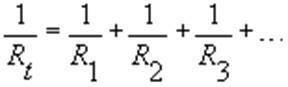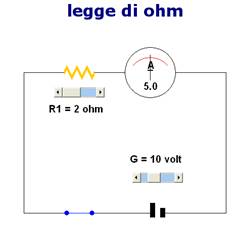
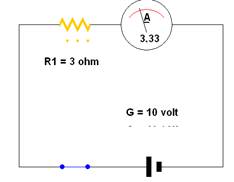
R1= 2Ω    Intensità = 5,0 A          R2= 3Ω          Intensità = 3,33 A
Aumentiamo solo il valore della Resistenza     R
                         
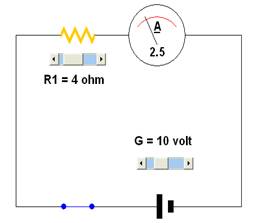
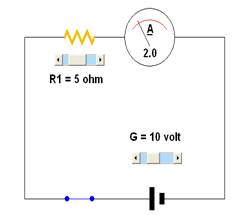
   R1= 4Ω Intensità = 2,5 AR1= 5ΩIntensità = 2,0 A
Altri  esempi di esercizi   svolti
Esercizio n° 1
Due resistori in parallelo, da R1=R2 = 20 W ciascuno, vengono collegati ad un unico generatore di tensione avente la tensione V (generatore) = 12 Volt

Con la legge di Ohm ci calcoliamo la corrente totale del circuito:
Vt = Rt x It
Ricaviamo la formula inversa:
    It =  Vt =    12 V      =  1,20  A
            Rt       10Ω
Essendo tutti i componenti collegati parallelo avranno tutti la stessa tensione
V1 = V2 = V (generatore) =  12,00 V
Non resta ora che calcolare le due correnti dei due resistori:
I1 =      V1      =    12      =  0,60  A
            R1             20
I2 =      V2      =    12      =  0,60  A
            R2             20                                    Esercizio n ° 2
 
E =Generatore = 12 V
R1 = 1 W
R2 = 1.000 W
R3 = 1.000 W
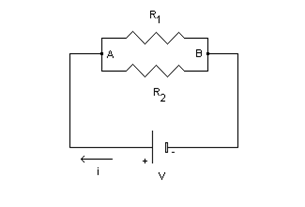
Notiamo che i resistori R2 ed R3 sono collegati in parallelo, in quanto tutti e due hanno i rispettivi terminali l'uno collegato al punto A e l'altro al punto B del circuito.
Poiché i due resistori R2 ed R3 sono in parallelo ci calcoliamo la loro resistenza equivalente Rp:
Rp =                             1                       =
                             1      +       1     .
                                R2                  R3 .
 
 =                1                       =  500 W
              1      +       1     .
              1000             1000 .
Sostituendo ai due resistori R1 ed R2 il loro parallelo Rp, il circuito diventa:

Circuito equivalente a quello iniziale
Ci calcoliamo, ora la resistenza totale; notiamo che R1 ed Rp sono in serie, quindi la loro resistenza equivale alla seguente:
Rt = R1 + Rp = 1 + 500 = 501 W
Il circuito, ora è il seguente: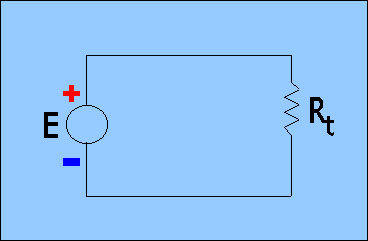
Con la legge di Ohm ci calcoliamo la corrente totale del circuito.
Vt = Rt x It
Ricaviamo la formula inversa:
It =       Vt      =    12      =  0,023952  A
               Rt           501

La corrente totale circola nella resistenza totale Rt  .
Riconsideriamo, ora, il circuito equivalente precedente:

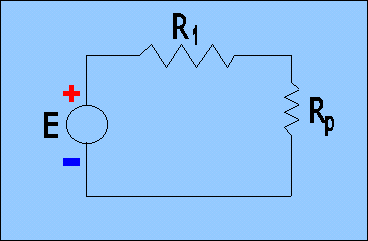
Circuito equivalente a quello iniziale
 
La corrente sarà uguale in tutti i componenti del circuito e in particolare in R1 e in Rp. Quindi possiamo scrivere:
I1 = Ip = It = 0,023952 A
A questo punto ci possiamo calcolare le due tensioni esistenti ai capi di R1 e ai capi del parallelo Rp, utilizzando la legge di Ohm. Otteniamo, allora:
V1 = R1 x I1= 1 x 0,023952 = 0,023952 V
mentre per V p  otteniamo:
V p = Rp x Ip = 500 x 0,023952 = 11,976 V
Ma poiché Rp rappresenta il parallelo dei due resistori R2 ed R3, e sapendo che i resistori in parallelo hanno la stessa tensione, possiamo scrivere:
V2 =V3 =V p = 11,976 V
Applicando ora la formula inversa della legge di Ohm ci possiamo calcolare le due correnti:
I2 =      V2   =    11,976   =  0,011976 A
               R2         1000
Analogamente per I3 otteniamo:
I3 =      V3      =    11,976   =  0,011976 A
              R3             1000
Più piccola è lo spessore del filo più grande è la resistenza R
Un altro elemento che influisce sulla legge di Ohm è il tipo di materiale e quindi la sua Resistività  in Wmm2/m capacità del materiale di opporsi al fluire in esso della corrente elettrica.
Rame =                  0,016  Wmm2/m                         Tugsteno=0,05  Wmm2/m                        
Alluminio =            0,026 Wmm2/m                           Piombo = 0,20  Wmm2/m                        

Applicazione  della formula I = V / R
ESERCIZI                     IL valore V  è sempre costante  ed è pari a  9V
IL valore della R  diminuisce     18Ω , 15 Ω , 12 Ω, 9 Ω, 6 Ω, 3 Ω,
1° esempio  I =  9V/18 Ω  = 0,50 A
2° esempio I =9V/15= 0,60 A
Continuare  con  i seguenti valori di Hom 14 Ω,12 Ω, 9 Ω, 6 Ω, 3 Ω,1 Ω
Applicazione  della seguente  formula  **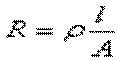             
ESERCIZI
Applicate  i valori di    del rame, dell’alluminio,del  tugsteno e del piombo.
ESERCIZI
l =  10 m  in mm 10000 
Invece dell’area A mettere lo spessore in mm ____    2mm, 4mm, 6mm, 8 mm.
Svolgimento:     R = 0,016 x 10000/2= 80 Ω
8 m, 6m, 5m, 4m, 2m;
Applicando i valori       della tabella di pag 5
Applicate la formula ** variando prima  la lunghezza , poi lo spessore, poi i due valori insieme,   considerando  che ogni esercizio  si deve cambiare il tipo di materiale.

 

Fonte: http://www.dantealighieritorino.it/realizzazioni/didattica/amato/Tesina%20sull'Elettricita.doc

Sito web da visitare: http://www.dantealighieritorino.it/

Autore del testo: non indicato nel documento di origine

Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.

 

Elettricità

 

 

I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

Elettricità

 

"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco

www.riassuntini.com dove ritrovare l'informazione quando questa serve