Materiali ferromagnetici

 

 

 

I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore

 

 

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

 

 

 

Materiali ferromagnetici

MATERIALI MAGNETICI

Lez. 14a                         Lez. 1 della Parte 3a

COMPORTAMENTO MAGNETICO DEI MATERIALI

OBIETTIVI DELLA LEZIONE 3.1

Richiamare le relazioni principali sul magnetismo.

Presentare e classificare i fenomeni magnetici nei materiali.

Fornire una spiegazione qualitativa di tali fenomeni.

MATERIALI FERROMAGNETICI

Costituiscono i circuiti magnetici e gli elementi di schermatura magnetica nei componenti a funzionamento elettromagnetico

RICHIAMI DI MAGNETISMO

Ricordiamo che se si pone:

B = vettore induzione magnetica

H = vettore intensità del campo magnetico

nel vuoto possiamo porre:

B = mo H

La costante mo si chiama permeabilità magnetica del vuoto e nel sistema di misura SI abbiamo:

 

mo = 4 p 10-7 H/m

 

in pratica approssimato a:

mo = 1,26 10-6 H/m

 

In presenza di un qualunque materiale si può porre:

 

B = mr moH

 

dove si ha:

mr = permeabilità relativa del materiale.

e da un punto di vista quantitativo abbiamo:

mr < 1, per materiali diamagnetici.

mr > 1, per materiali paramagnetici. 

mr >> 1, per materiali ferromagnetici e ferrimagnetici.

Tenendo conto che, salvo che per i materiali ferromagnetici e ferrimagnetici, mr  è  sempre molto prossima ad 1.

Si può inoltre definire un vettore M  intensità di magnetizzazione:

M = (B - Bo)/m0

 

dove Bo è l’induzione nel vuoto e B l’induzione che si stabilisce quando si sostituisce al vuoto un qualunque  materiale.

Si può anche porre:

 

B = m0 (H + M)

 

Dove M rappresenta il momento magnetico per unità di volume del materiale.  Si può anche porre:

 

B= m0 (H + M)

 

Si definisce suscettività magnetica la quantità:

cm = M/H

 

Dalle relazioni precedenti si ottiene:

 

cm = (mr - 1)

 

Per materiali diamagnetici si ha M < 0,.

Nel vuoto si ha M = 0, c = 0.

Per materiali paramagnetici si ha M > 0, c > 0.

Per i materiali ferromagnetici e ferrimagnetici si ha M >> 0, c >> 0.

Solamente i materiali ferromagnetici e ferrimagnetici hanno importanza pratica nell’industria elettrica.

 

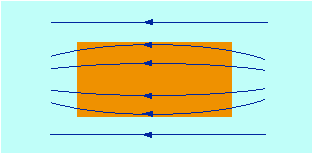
Fig. 14.1 - Materiali diamagnetici.

 

Il campo magnetico viene indebolito all’interno del materiale. sono diamagnetiche tutte le sostanze. l’effetto è molto debole (mr circa 1, c  circa 10-6), è  mascherato dal paramagnetismo e dal ferromagnetismo (Figg. 14.1, 14.2 e 14.3).

In un materiale diamagnetico non esistono dipoli magnetici permanenti. l’applicazione di un campo magnetico di induzione B crea dei dipoli magnetici di direzione opposta e quindi tali da indebolire B.

Fig. 14.2 - Materiale diamagnetico in assenza di campo magnetico esterno.

 

Fig. 14.3 - Materiale diamagnetico in presenza di un campo magnetico  esterno.

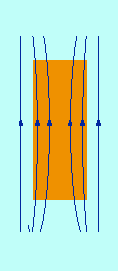
Fig. 14.4 - Materiali paramagnetici.

 

Il campo magnetico viene rafforzato all’interno del materiale. l’effetto è piuttosto debole (mr circa 1, c = 10-6 - 10-2) anche se tale da mascherare il comportamento diamagnetico (Fig. 14.4).

nei materiali paramagnetici sono presenti dipoli magnetici permanenti di tipo atomico:

Per B = 0  i dipoli non hanno una direzione preferenziale;

Per  B diverso da zero i dipoli tendono ad orientarsi nella direzione del campo rafforzandolo.

Il fenomeno è disturbato dall’agitazione termica

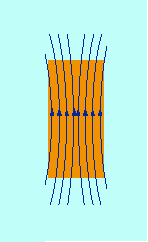
Fig. 14.5 - Materiali ferromagnetici.

Si ha un effetto simile a quello dei materiali paramagnetici ma molto rafforzato (mr dell’ordine di alcune migliaia o decine di migliaia) (Fig. 14.5). I dipoli permanenti sono raggruppati in domini (detti domini di Weiss) i cui momenti magnetici non sono concordi fra loro per valori nulli o molto bassi di B.Se B cresce aumentano le dimensioni dei domini concordi con il campo e si ha rotazione rigida di altri domini (Figg. 14.6 e 14.7).

 

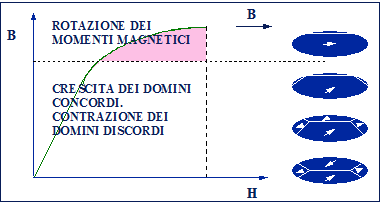
Fig. 14.6 - Crescita e rotazione dei domini magnetici.

Fig. 14.7 - Spostamento delle pareti dei domini per effetto del campo magnetico esterno.

RIEPILOGO DELLA LEZIONE 3.1

Sono state richiamate le relazioni generali sul magnetismo nei materiali.

Sono stati brevemente descritti i materiali:

diamagnetici

paramagnetici

ferromagnetici

Lez. 15a                         Lez. 2 della Parte 3a

MATERIALI FERRIMAGNETICI, ANTIFERROMAGNETICI E
FERROMAGNETICI

OBIETTIVI DELLA LEZIONE 3.2

Presentare i materiali ferrimagnetici ed antiferromagnetici.

Descrivere da un punto di vista macroscopico il comportamento dei materiali ferromagnetici.

Presentarne le proprietà di interesse tecnico.

MATERIALI ANTIFERROMAGNETICI

Sono materiali per i quali l’accoppiamento dei dipoli magnetici è rigorosamente antiparallelo. Si comportano come materiali paramagnetici al disopra di una certa temperatura detta temperatura di Néel (Fig. 15.1).

MATERIALI FERRIMAGNETICI

In questi materiali sono presenti ioni con diverso momento magnetico. si hanno quindi effetti esterni intermedi fra i materiali ferromagnetici e quelli antiferromagnetici. Anche in questo caso al disopra di una certa temperatura il materiale diviene paramagnetico (Fig. 15.1).

Sono ferrimagnetici alcuni materiali ceramici chiamati ferriti. essi hanno un valore di permeabilità magnetica relativa dell’ordine delle decine o delle centinaia.

 

Fig. 15.1 - Schematizzazione di domini di materiali ferromagnetici, antiferromagnetici e ferrimagnetici.

MATERIALI CON DIVERSO COMPORTAMENTO MAGNETICO.

DIAMAGNETICI: bismuto, rame, argento, stagno, zinco.

PARAMAGNETICI: alluminio, calcio, ossigeno, platino.

FERROMAGNETICI: ferro, cobalto, nichel.

ANTIFERROMAGNETICI: MnO2.

FERRIMAGNETICI: magnetite.

 

CARATTERIZZAZIONE DI UN MATERIALE FERROMAGNETICO.

Definiamo curva di magnetizzazione di un materiale (Figg. 15.3 e 15.4) la curva di B in funzione di H. Questa curva può essere determinata sperimentalmente usando un toro di materiale ferromagnetico (Fig. 15.2).

Fig. 15.2 Circuito per la determinazione della curva di magnetizzazione di un materiale.

 

Si ottiene quindi il valore del campo:

H = N1 IM/2p r

La tensione indotta al secondario vale:

 

e2= N2DF/Dt = N2BA /Dt

Si ottiene quindi  il corrispondente valore dell’induzione magnetica:

 

B = e2 Dt / N2A

Dove A è la sezione del toro.

Se chiudiamo il secondario su una resistenza R circolerà, per un tempo Dt, una corrente i2 pari a:

 

i2 = e2/R

si ha quindi:

 

B = e2Dt/N2A = i2RDt/N2A = qR/N2A

dove q è la carica che fluisce in R nel tempo Dt. Tale carica si può misurare con un galvanometro balistico.

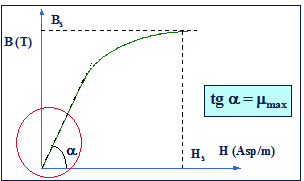
Fig. 15.3 - Curva di prima magnetizzazione di un materiale ferromagnetico

Fig. 15.4 - Tratto iniziale della curva di prima magnetizzazione

 

L’andamento del tratto iniziale della curva B - H si può spiegare con un ritardo dei domini ad orientarsi nella direzione del campo magnetico.

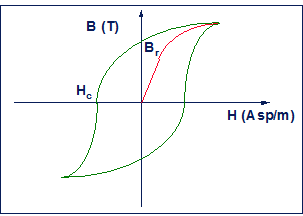
Fig. 15.5 - Ciclo di isteresi di un materiale ferromagnetico

 

Il fenomeno dell’isteresi in un materiale ferromagnetico (Fig. 15.5) si può spiegare con il fatto che per B = 0 non tutti i domini ritornano all’orientamento iniziale. L’isteresi magnetica produce delle perdite la cui entità è proporzionale  all’area del ciclo. L’orientamento dei domini avviene in modo discontinuo (Fig. 15.6).

PROPRIETÀ DEI MATERIALI FERROMAGNETICI

Le proprietà dei materiali ferromagnetici di interesse applicativo sono:

L’induzione di saturazione Bs

Il campo di saturazione Hs

La permeabilità massima mmax 

La permeabilità iniziale mi

Risultano inoltre di particolare interesse per i magneti permanenti:

l’induzione residua Br

la forza coercitiva Hc

 

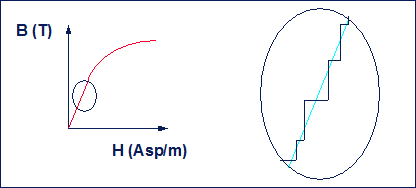
Fig. 15.6 - Orientamento dei domini di Weiss per effetto del campo

RIEPILOGO DELLA LEZIONE 3.2

Abbiamo presentato i materiali antiferromagnetici e ferrimagnetici

Abbiamo introdotto la curva di prima magnetizzazione ed il ciclo di isteresi.

Sono state elencate le proprietà dei materiali ferromagnetici.

 

 

 

Lez. 16a                         Lez. 3 della Parte 3a

MATERIALI FERROMAGNETICI, APPLICAZIONI

CON FLUSSO COSTANTE.

OBIETTIVI DELLA LEZIONE 3.3

Presentare i materiali ferromagnetici  dolci e duri (Figg. 16.1 e 16.2).

Descrivere i metalli elementari dotati di proprietà ferromagnetiche.

Considerare le applicazioni di materiali ferromagnetici in presenza di flusso costante.

 

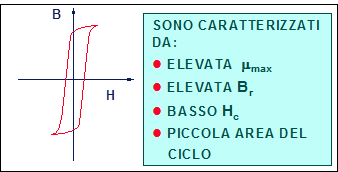
Fig. 16.1 - Materiali ferromagnetici dolci.

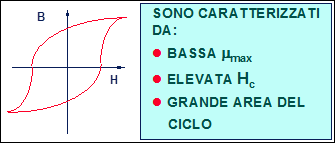
Fig. 16.2 - Materiali ferromagnetici duri.

ELEMENTI FERROMAGNETICI

    Gli elementi ferromagnetici sono:

Ferro

Cobalto

Nickel

FERRO

È l’unico elemento utilizzato allo stato puro come materiale ferromagnetico. presenta perdite per isteresi ridotte. Si smagnetizza facilmente. È il componente fondamentale di molte leghe ferromagnetiche (Figg. 16.3, 16.6 e 16.7).

 

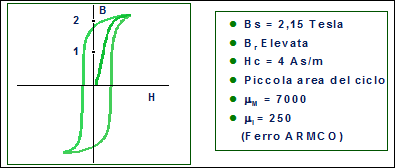
Fig. 16.3 - Caratteristiche magnetiche del ferro

NICHEL

Si tratta di un materiale non interessante allo stato puro. Le sue proprietà dipendono molto dai trattamenti e dalle lavorazioni. è costituente di molte leghe (Figg. 16.4, 16.6 e 16.7).

 

Fig. 16.4 - Caratteristiche magnetiche del nichel.

COBALTO

È un materiale con perdite per isteresi elevate. non è usato allo stato puro, ma rientra in leghe magnetiche, specie per magneti permanenti. Anche il cobalto è molto sensibile ai trattamenti termici (Figg. 16.5, 16.6 e 16.7).

 

 

Fig. 16.5 - Caratteristiche magnetiche del cobalto.

Fig. 16.6 - Curve di prima magnetizzazione di ferro, nichel, cobalto.

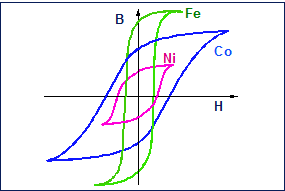
Fig. 16.7 - Cicli di isteresi di ferro, nichel, cobalto.

APPLICAZIONI DEI MATERIALI FERROMAGNETICI

Nuclei magnetici massicci

Nuclei magnetici laminati

Magneti permanenti

Componenti ad alta frequenza

Schermi magnetici

NUCLEI MAGNETICI MASSICCI

Si riferiscono a parti di circuiti magnetici sede di flussi magnetici costanti nel tempo

Gioghi rotorici e poli di macchine sincrone

Gioghi statorici e poli di macchine a commutazione

Nuclei di elettromagneti e relé in corrente continua

Per i nuclei massicci si usano:

Ferro lavorato

Acciaio al carbonio (0,1 - 1% C):

Fuso

Fucinato

In lamiere spesse

Ghisa (2 - 4,6% C):

Grigia

Malleabile

Duttile

Per queste applicazioni interessano in modo particolare (Fig. 16.7):

 I valori delle permeabilità massima ed iniziale.

La forma del ciclo di isteresi

L’induzione di saturazione

La forza coercitiva

Fig. 16.7 - Curve di magnetizzazione di ferro, acciaio e ghisa

PROPRIETÀ MECCANICHE

    Sono spesso determinanti nelle macchine rotanti:

Rotori dei turboalternatori

Gioghi di rotore e delle macchine sincrone a poli salienti

In questi casi si usa di regola acciaio fucinato

L’aggiunta di carbonio al ferro aumenta Hc, diminuisce mM ,cioè indurisce il materiale.

L’aggiunta di una quantità di nichel > 25% dà luogo ad un acciaio inossidabile non ferromagnetico

Possono essere considerati   materiali massicci anche i lamierini spessi utilizzati per i poli delle macchine sincrone (fino a 2mm) e per i gioghi rotorici delle macchine sincrone ad ombrello (fino a 5mm).    

RIEPILOGO DELLA LEZIONE 3.3

Sono stati presentati i materiali ferromagnetici dolci e duri.

Abbiamo descritto il comportamento magnetico di ferro, cobalto e nichel.

Sono stati considerati i campi di applicazione di ferro, acciaio e ghisa utilizzati sotto forma di materiali massicci.

Lez. 17a                    Lez. 4 della Parte 3a

MATERIALI FERROMAGNETICI IN PRESENZA DI FLUSSO VARIABILE.

OBIETTIVI DELLA LEZIONE 3.4

Descrivere i fenomeni che si verificano nei materiali ferromagnetici soggetti a flusso variabile nel tempo.

Considerare gli accorgimenti atti a limitare gli effetti negativi di tali fenomeni.

MATERIALI FERROMAGNETICI SOGGETTI A FLUSSO VARIABILE

In un materiale ferromagnetico sede di un flusso variabile è importante considerare i seguenti fenomeni:

Magnetostrizione

Perdite per isteresi

Perdite per correnti parassite

MAGNETOSTRIZIONE

Un materiale ferromagnetico magnetizzato cambia leggermente le sue dimensioni. si produce cioè una variazione reversibile  Dl/l  dell’ordine di 10-6. Il fenomeno della magnetostrizione riveste più che altro un interesse in presenza di campi magnetici costanti. Produce, invece, con campi variabili nel tempo, fenomeni vibratori ed emissioni sonore difficilissime da eliminare (Fig. 17.1).

 

Fig. 17.1 - Magnetostrizione in un materiale ferromagnetico.

La magnetostrizione è attribuita al cambiamento della lunghezza dei legami atomici quando i momenti di dipolo elettronici in un dominio ruotano per effetto del campo. I campi dei dipoli possono attrarsi, ed il metallo si contrae (magnetostrizione negativa), o respingersi, ed il metallo si dilata (magnetostrizione positiva) (Figg. 17.1 e 17.2).

 

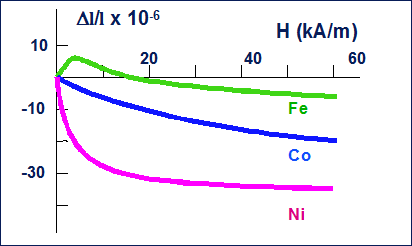
Fig. 17.2 - Magnetostrizione in ferro, cobalto e nichel.

PERDITE NEI MATERIALI FERROMAGNETICI

La potenza dissipata nei materiali ferromagnetici, a causa delle variazioni del flusso, costituisce una delle voci principali di cui tenere conto nella valutazioni del rendimento delle macchine elettriche.

PERDITE PER ISTERESI

In presenza di un campo variabile è necessario fornire energia per consentire le continue variazioni di orientamento dei domini. L’energia per unità di volume necessaria per portare un materiale all’induzione Bvale:

 

pi = ki f BM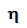 
dove si è posto:

PERDITE PER CORRENTI PARASSITE

Sono perdite prodotte da correnti che, nella massa di un conduttore ferromagnetico, circolano su piani ortogonali alla direzione del vettore B, che, ricordiamo, è variabile nel tempo (Fig. 17.3).

 

Fig. 17.3 - Correnti parassite in un materiale ferromagnetico conduttore

sipossono calcolare queste perdite con la seguente relazione:

pc = kc f2 B M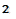

dove si  è posto:

kc dipende dalla resistività r  del materiale e dalla sezione S perpendicolare alla direzione di B.
Per ridurre pc è necessario aumentare r e ridurre S.
Le perdite in un materiale ferromagnetico soggetto a campo variabilepossono quindi essere determina conla seguente relazione:

pf = pi + pc = ki f BM + kc f 2 BM

Spesso si può anche porre con buona approssimazione:

pf = kf B M 2

RIDUZIONE DELLE PERDITE NEL FERRO

Interventi per ridurre le perdite nei materiali ferromagnetici:

modificare le caratteristiche del materiale per :

ridurre l’area del ciclo di isteresi

aumentarne la resistività

usare lamierini sottili

RIDUZIONE DELL’AREA DEL CICLO DI ISTERESI

Si ottiene con i seguenti interventi:

agendo sulla composizione del materiale

attraverso trattamenti di ricottura o comunque rivolti a modificare la struttura del materiale.

 

Fig. 17.4 - Correnti parassite in un nucleo ferromagnetico laminato.

AUMENTO DELLA RESISTIVITÀ DEL MATERIALE

Si ottiene con i seguenti interventi:

agendo sulla composizione del materiale

attraverso trattamenti termici

creando discontinuità elettriche

USO DI LAMIERINI SOTTILI

Si usano lamierini dello spessore di 0,5 - 0,35 mm posti in modo da opporsi alla circolazione delle correnti parassite (Fig 17.4).

In alternativa si potrebbero usare fili (di impiego problematico) o polimeri caricati (bassa m)

 

RIEPILOGO DELLA LEZIONE 3.4

Abbiamo considerato il fenomeno della magnetostrizione.

Abbiamo determinato le perdite per isteresi e per correnti parassite.

È stato giustificato l’uso di materiali laminati in presenza di campi tempovarianti.

Lez. 18a               Lez. 5 della Parte 3a

PERDITE NEI MATERIALI FERROMAGNETICI - LAMIERINI AL SILICIO.

OBIETTIVI DELLA LEZIONE 3.5

Valutare quantitativamente le perdite.

Descrivere  le proprietà dell’acciaio al silicio.

Considerare i diversi tipi di lamierini usati negli apparati elettromeccanici.

 

CIFRA DI PERDITA

In pratica il valore delle perdite di un materiale ferromagnetico viene fornito attraverso la cifra di perdita pm così definita:

 

POTENZA PERDUTA IN UN CHILOGRAMMO DI MATERIALE. ESPRESSA IN WATT/kg, CON

B = 1 TESLA, f = 50 Hz,

Se G è il peso del materiale soggetto all’induzione di 1 T le perdite valgono:

Pm = k pmG (watt)

dove k > 1 tiene conto del tipo di montaggio del nucleo magnetico. se si ha:

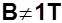
si può, in prima approssimazione scrivere:
Pm = k pmG B2 (watt)

per un calcolo più preciso occorre usare un diagramma delle perdite in funzione di B (Fig. 18.1 e 18.2).

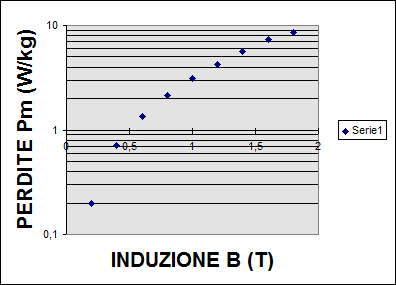
Fig. 18.1 - Perdite in funzione di B in un materiale ferromagnetico

 

 

 

FIG. 18.2 - Perdite in funzione di B2 in un materiale ferromagnetico

Tab. 18.1.

Il margine di riduzione delle perdite per isteresi è piuttosto ridotto, si producono lamierini con cristalli superorientati con cicli di isteresi molto ristretti con tecniche di degasaggio sotto vuoto e con particolari trattamenti si riducono i tenori di O, N, S.

Tab. 18.2.

Si hanno ancora notevoli margini di azione considerando che nei lamierini ad alta permeabilità le perdite anomale pesano circa per il 40% del totale. Si  agisce in due direzioni:

MATERIALI FERROMAGNETICI LAMINATI

Si tratta di lamierini in acciaio a cui si aggiunge silicio fino ad un massimo del 4 - 4,5 %. L’aggiunta di silicio produce i seguenti vantaggi:

mr = 7000 per un acciaio al 3% Si

Evita l’invecchiamento magnetico

Svantaggi prodotti dall’aggiunta di silicio:

LAMIERINI FERROMAGNETICI

I principali tipi di lamierini ferromagnetici sono:

Lamierini a cristalli non orientati.

Lamierini a cristalli orientati.

Lamierini a cristalli superorientati.

Lamierini magnetici amorfi.

Lamierini microcristallini.

LAMIERINI A CRISTALLI NON ORIENTATI (Tab. 18. 3).

Si hanno i seguenti tipi:

Lamiere da dinamo, acciaio extradolce.

Lamiere semilegate (1-1,5% Si)

Lamiere legate (2-2,5% Si)

Lamiere extralegate (3,5% Si)

Tab. 18.3 - Caratteristiche di lamierini a cristalli non orientati

LAMIERINI A CRISTALLI ORIENTATI

Con ripetute laminazioni a freddo intervallate da trattamenti di ricottura si ottengono lamierini in cui i domini hanno i momenti magnetici concordemente orientati nella direzione di laminazione (Fig. 18.3).

Si ottengono lamierini con cifra di perdita inferiore a 0,75 W/kg (0,4 - 0,6 W/kg).

Con elevata permeabilità (mmax = 30.000, mi = 1.500).

Induzione di saturazione leggermente superiore a quella dei lamierini a cristalli non orientati (Bs = 2 T)

Fig. 18.3 - Perdite e permeabilità relativa in un lamierino a cristalli orientati in funzione dell’angolo  di laminazione.

 

I lamierini a cristalli orientati sono impiegati in tutti quei circuiti magnetici nei quali il flusso abbia una direzione prevalente. cioè:

nei nuclei dei trasformatori

negli statori dei grandi turboalternatori, con orientamento circonferenziale.

I lamierini a cristalli orientati sono disponibili in rotoli alti 1m. la loro superficie è isolata con isolamento minerale e può essere successivamente verniciata. dopo tranciatura viene effettuato un trattamento di ricottura.

RIEPILOGO DELLA LEZIONE 3.5

È stato introdotto il concetto di cifra di perdita.

Sono stati descritti lamierini isotropi al silicio.

Sono stati descritti i lamierini a cristalli orientati e sono stati presentati i principali campi di impiego.

Lez. 19a               Lez. 6 della Parte 3a

LAMIERINI MAGNETICI, FERRITI.

 

OBIETTIVI DELLA LEZIONE 3.6

Considerare alcuni problemi legati all’impiego dei lamierini a cristalli orientati.

Presentare i lamierini ferromagnetici di tipo innovativo.

Descrivere i materiali ad elevata permeabilità e per alta frequenza.

 

CAMPI DI IMPIEGO DEI LAMIERINI A CRISTALLI ORIENTATI:

Nei nuclei dei trasformatori (Figg. 19.1 e 19.2).

Negli statori dei grandi turboalternatori, con orientamento circonferenziale dei lamierini (Fig. 19.3).

 

 
Fig. 19.1

 

Fig. 19.2

 

 

 

Fig. 19.3 - Utilizzazione dei lamierini a cristalli orientati nello statore di un turboalternatore.

LAMIERINI A CRISTALLI SUPERORIENTATI.

Sono lamierini ad alta permeabilità (HI - B) o sui quali sono stati effettuati interventi volti ad ottenere domini magnetici di minori dimensioni e con struttura più regolare (Fig. 19.4).

Fig. 19.4 - Perdite specifiche in funzione dello spessore in un lamierino HI - B trattato con il laser.

LAMIERINI MAGNETICI AMORFI

Sono i lamierini commerciali con la più bassa cifra di perdita (0,1 W/kg).

Si tratta di leghe a base di ferro, boro, silicio.

Sono molto sottili ( fino a 20 mm).

Hanno alta permeabilità

Sono ottenuti producendo un nastro con velocità di raffreddamento dell’ordine di 105 -106 oC/s. Si impedisce così la cristallizzazione della lega. L’unica lega in commercio ha composizione:

Fe 78% B13% Si 9%

 

hanno le seguenti caratteristiche principali:

 elevata permeabilità, mmax fino a 600.000;

 bassa Bs (intorno a  1,55 T)

 basse perdite(1/3, 1/4 dei lamierini normali)

 elevata magnetostrizione (fino a 30 10-6)

I lamierini magnetici amorfi ono usati per nuclei avvolti o per piccoli componenti.

LAMIERINI MICROCRISTALLINI

Sono fabbricati con la tecnica dei materiali amorfi ma con raffreddamento più lento.

Si sono ottenuti lamierini Fe - Si con percentuali fino al 6% Si  con cifra di perdita non molto superiore a quella dei materiali amorfi. Si tratta di materiali sperimentali.

LEGHE FERRO NICHEL

La presenza del nichel nelle leghe ferrose causa un forte aumento della permeabilità iniziale e della permeabilità massima. si ha una induzione di saturazione piuttosto bassa. Con il 30% di nichel si ottiene una lega non ferromagnetica (Figg. 19.5 e 19.6, Tab. 19.1).

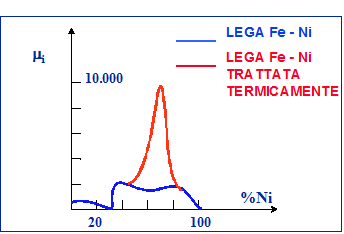
Fig. 19.5 - Permeabilità iniziale della lega Fe-Ni in funzione della % di Ni.

 

 

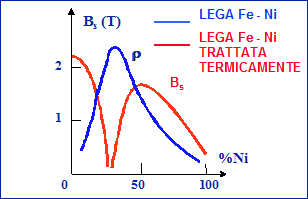
Fig. 19.6 - r e Bs della lega Fe-Ni in funzione della % di Ni.

Tab. 19. 1 - Caratteristiche delle principali leghe Fe - Ni.

APPLICAZIONI DELLE LEGHE Fe - Ni

Sono usate anche in spessori molto sottili:

per trasformatori di misura per ridurre i flussi dispersi;

in trasformatori ed apparati a frequenze audio;

in applicazioni per telecomunicazioni.

LEGHE FERRO - COBALTO

Il cobalto è un materiale duro. Oltre che per i magneti permanenti le leghe Fe - Co consentono di ottenere elevata Bs (permendur) o costanza di m nel tratto iniziale della curva di magnetizzazione (perminvar) (Tab. 19.2).

La lega permendur è dura e fragile, non si lavora a freddo. Per la Bs elevata si usa per poli di elettromagneti.

La lega perminvar è utilizzata in telecomunicazioni e strumenti di misura.

Tab. 19.2 - Caratteristiche di leghe Fe - Co e di una ferrite Mn - Zn.

FERRITI

Sono materiali ferrimagnetici non metallici costituiti da ossidi di ferro e di un metallo bivalente (Mg, Mn, Zn, Cu, .....).

Possono essere considerati sali di un ipotetico acido ferrico.

Sono assimilabili a materiali ceramici dei quali hanno la durezza e la fragilità.

Anche la tecnologia è tipica dei materiali ceramici.

Hanno conducibilità molto bassa e quindi perdite molto ridotte.

Sono quindi utilizzabili in alta frequenza.

Le ferriti più comuni sono del tipo Mn - Zn, Ni - Zn, Mg - Mn.

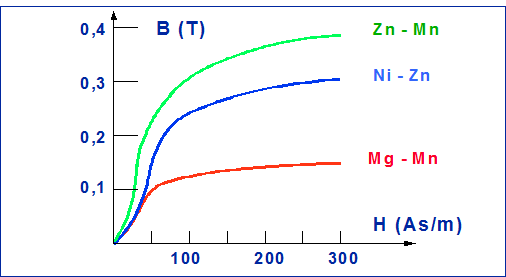
Fig. 19.7 - Curve di magnetizzazione di alcune ferriti.

Anche i granati sono materiali ferrimagnetici utilizzati in alta frequenza, ad es. per testine di registrazione, nuclei per antenne. La ferrite più comune è il TIPO Mn - Zn usata fino ad 1,5 Mhz. Oltre 1,5 MHz si usano ferriti  Ni - Zn. Ricordiamo infine che per particolari scopi possono essere impiegati polimeri caricati con polveri ferromagnetiche.

 

RIEPILOGO DELLA LEZIONE 3.6

È stato considerato l’uso di lamierini a cristalli orientati nelle macchine elettriche.

Sono stati presentati lamierini di tipo innovativo.

Sono stati descritti i materiali ad alta permeabilità e per alta frequenza.

 

Lez. 20a               Lez. 7 della Parte 3a

DIMENSIONAMENTO DI UN CIRCUITO MAGNETICO

 

OBIETTIVI DELLA LEZIONE 3.7

Fornire gli elementi essenziali per il dimensionamento di un circuito magnetico, considerando sia il caso di flusso costante che il caso di flusso variabile nel tempo

CIRCUITO MAGNETICO

Si definisce circuito magnetico quella parte di una macchina a funzionamento elettromagnetico, che costituisce il  volume preferenziale dove si stabilisce il flusso di induzione magnetica necessario al suo funzionamento. Un circuito magnetico è sede di linee di flusso chiuse ed costituito da tratti, posti in serie, che possono essere considerati tubi di flusso. Alcuni di questi tratti possono essere costituiti da materiali non ferromagnetici e sono chiamati traferri o interferri (Fig. 20.1).

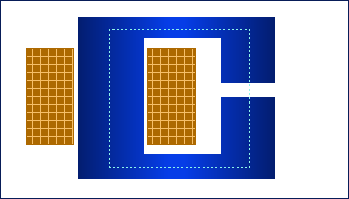
Fig. 20.1 - Circuito magnetico di un magnete con traferro.

DIMENSIONAMENTO DI UN CIRCUITO MAGNETICO

Si possono considerare due casi tipici:

circuiti magnetici soggetti a flusso costante nel tempo;

circuiti magnetici soggetti a flussi tempovarianti (di solito sinusoidali).

SCOPI DEL PROGETTO DI UN CIRCUITO MAGNETICO

determinare le sezioni e le lunghezze dei diversi tratti in serie;

determinare il peso del materiale ferromagnetico necessario;

determinare la f.m.m. necessaria per stabilire il flusso di induzione magnetica richiesto;

determinare il flusso disperso;

nel caso di presenza di flusso variabile nel tempo determinare le perdite nel materiale ferromagnetico.

DIMENSIONI E PESO DEL CIRCUITO MAGNETICO

Se si suppone che il circuito magnetico sia un tubo di flusso si ha flusso costante in tutti i tratti del circuito stesso.

Si suddivide il circuito in tratti nei quali l’induzione possa essere considerata costante o con andamento noto (Fig. 20.2).

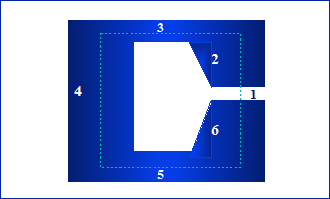
Fig. 20.1 -  Magnete con traferro.

Lungo i tratti 3, 4, 5, b, a parte le dispersioni, può essere considerata costante, mentre varia linearmente lungo i tratti 2 e 6. Nel tratto 1 (traferro) si ha un allargamento delle linee di flusso nelle zone periferiche (Figg. 20.3 e 20.4).

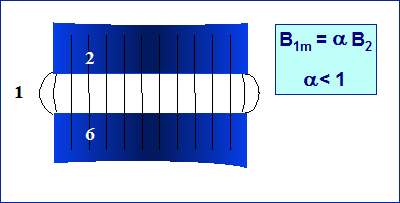
Fig. 20.3 - Determinazione di Bm  al traferro

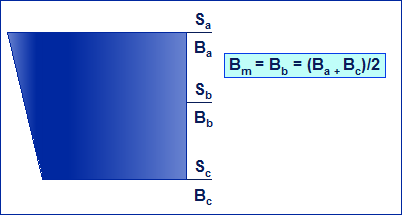
Fig. 20.4 - Determinazione di Bm in un tratto con sezione variabile linearmente.

Nel caso in fig. 20.2  il dato di partenza è il valore di B1 e della sezione S1. Si può così ottenere il flusso nel tratto 1.

F = ( B1 x S1) / a

Se si trascurano le dispersioni è quindi noto il flusso F uguale in tutte le sezioni del circuito magnetico. poiché ci proponiamo di fornire i lineamenti base di dimensionamento, nel seguito trascureremo, per semplicità, il flusso disperso di cui è sempre necessario tenere conto. Rinviamo ai corsi di progettazione dei componenti elettromeccanici la valutazione dell’entità dei fenomeni di dispersione. Si fissa una B ammissibile nella sezione minore (la 3 nell’esempio proposto) sulla base del livello di saturazione tollerato ed in funzione dello sfruttamento prefissato del materiale. Tale valore corrisponde nel nostro caso a B3. Si ha quindi:

S3 = F / B3

Se si suppone che le proporzioni fra le diverse sezioni siano  un dato di progetto è possibile determinare le diverse sezioni ed i corrispondenti valori di B, tenendo conto che F è uguale in ogni sezione. Si ha quindi per una generica sezione:

SN = F / BN

Infine si fissano le lunghezze dei diversi tratti in base alle esigenze di progetto ed alle dimensioni dei circuiti elettrici che devono essere inseriti nel componente da dimensionare (Tab. 20.1).

Fig. 20.1 - Dimensioni ed induzione nel circuito magnetico di Fig. 20.2.

Note le sezioni e le lunghezze si trova facilmente il volume V del circuito magnetico da cui, con il peso specifico g del materiale ferromagnetico, si determina il peso del circuito magnetico:

G = g V

DETERMINAZIONE DELLA f.m.m.

Per dimensionare il circuito di eccitazione del magnete è necessario conoscere il valore della f.m.m. necessaria per stabilire nel circuito magnetico il flusso richiesto. Per determinare la f.m.m. si applica le legge della circuitazione ad una linea di flusso nel circuito magnetico da dimensionare. Si ha quindi:

Poiché è di solito molto difficile calcolare l’integrale si preferisce suddividere il circuito in tratti nei quali l’induzione possa essere considerata costante o con andamento noto. Si trasforma allora l’integrale in una sommatoria estesa a tali tratti:

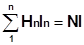
Per determinare H essendo noti i valori di B si ricorre alla curva di magnetizzazione del materiale (Fig. 20.4). Nel caso di sezione variabile si può effettuare una media pesata dei tre valori di H corrispondenti ai tre valori di B. Si può porre:

Hmedio = (Hmax + 4Hm + Hmin) / 6

Fig. 20.4 - Determinazione di h in funzione di B

Per il traferro si ha:

B1 = moH1

Si può quindi costruire una tabella con i valori di B, i corrispondenti valori di H e le lunghezze dei diversi tratti necessarie per calcolare la sommatoria (Tab. 20.2).

Tab. 20.2 - Dimensioni ed induzione del  circuito magnetico di Fig. 20.2.

DETERMINAZIONE DELLE PERDITE

Nel caso di circuiti magnetici soggetti a flusso variabile si procede con un calcolo uguale a quello dei circuiti con flusso costante. è necessario tuttavia determinare anche la potenza dissipata nel materiale ferromagnetico, sia per valutazioni energetiche, che per la determinazione della temperatura del componente da progettare. Determinato il peso dei singoli tratti di circuito magnetico si può porre;

Pm = k pmG B2 (watt)

 

O più correttamente si ricorre ad un diagramma che fornisce le perdite specifiche in funzione dell’induzione (Fig. 20.5).

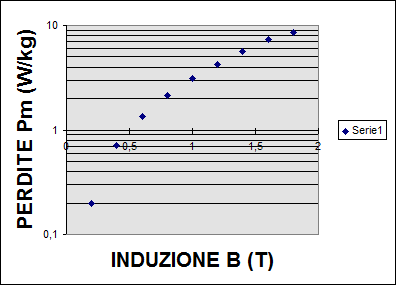
Fig. 20.5 - Perdite in funzione di B in un materiale ferromagnetico.

 

RIEPILOGO DELLA LEZIONE 3.7

Sono stati forniti gli elementi essenziali per il dimensionamento di un circuito magnetico.

È stata determinata la f.m.m. necessaria a stabilire il flusso.

Sono state determinate le perdite nel caso di flusso variabile nel tempo.

 

Lez. 21a               Lez. 8 della Parte 3a

MAGNETI PERMANENTI

OBIETTIVI DELLA LEZIONE 3.8

Descrivere le proprietà dei magneti permanenti.

Presentare i tipi di materiali più significativi.

Fornire i criteri generali per il loro uso.

MAGNETI PERMANENTI

Per costruire magneti permanenti è necessario impiegare materiali ferromagnetici duri (Fig. 21.1). E importante infatti disporre di forza coercitiva Hc ed induzione residua Br elevate (Fig. 21.2 e 21.3).

 

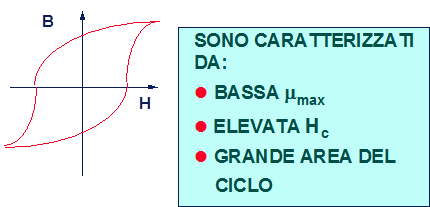
Fig. 21.1 - Materiali ferromagnetici duri.

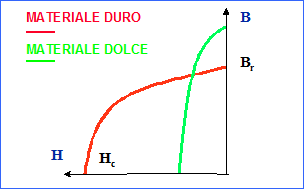
Fig. 21.2 - Parte del ciclo di isteresi interessante i magneti permanenti.

EQUAZIONI GENERALI DEI MAGNETI PERMANENTI
 
Fig. 21.3 - Magnete permanente senza traferro.
In un magnete permanente (Fig. 21.3) si ha:

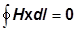
da cui consegue:
H=0
              

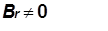
Pratichiamo adesso un trafero di ampiezza l0 (Fig. 21.4). Si ha allora:

Hf lf = - H0 l0

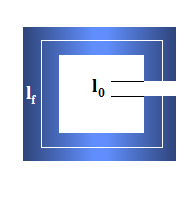
Fig. 21.4 - Magnete permanente con traferro.

 

Nel ferro si ha:

perciò nell’aria deve essere:
                  
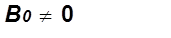
Ricordiamo d’altra parte l’espressione:
B0 = a Bf    a > 1

Per cui si determinano H0 ed Hf :
H0 = B0/m0             Hf = - H0 (l0/lf)
Da cui

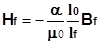
L’ultima espressione di hf in funzione di Bf è l’equazione di una retta con coefficiente angolare pari a:
- (al0) / (m0lf)

Si può quindi determinare sulla caratteristica del materiale scelto il punto di lavoro caratterizzato dai valori Hf, Bf (Fig. 21.5).

 

 

 

 

Fig. 21.5 - Determinazione del punto di lavoro di un magnete permanente

Osserviamo che si hanno le seguenti situazioni:

per         l0 = 0           Bf = Br          Hf = 0
per 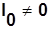                   Bf < Br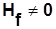              

CONSIDERAZIONI ENERGETICHE

L’energia magnetica al traferro vale:

 

W = 1/2 m0 H0 V0 = 1/2 m0 Hf (lf/l0)(B0/m0) l0 S0 = 1/2 Hf lf a Bf S0 

dove         V0 = volume del traferro

                 S0  = sezione del traferro

 

se si ha: S0 = Sf 

ed è:      Vf = volume del ferro

W = 1/2 a Vf Bf Hf

 

A parità di energia si che il volume del ferro è minimo quando il prodotto Bf Hf è massimo. si può così determinare il punto di lavoro più conveniente (Fig. 21.6).

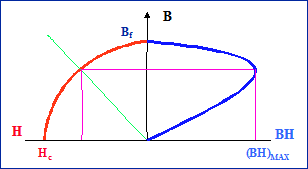
Fig. 21.6 - Punto di lavoro e prodotto di energia.

 

Se si ha una variazione del traferro o smagnetizzazione del magnete permanente che porti a variazioni di Hf e di Bf il materiale descrive dei cicli parziali che sono spesso assimilati a rette, chiamate rette di ritorno  (Fig. 21.7).

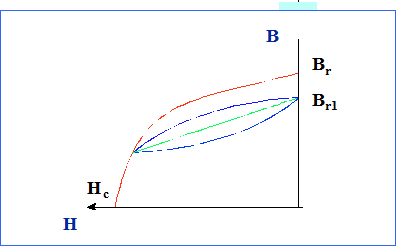
Fig. 21.7 - Retta di ritorno.

MATERIALI PER MAGNETI PERMANENTI

I materiali per magneti permanenti possono essere ottenuti con le seguenti tecnologie:

Per colata

Per sinterizzazione

Materiali ottenuti da polveri finissime

 

MATERIALI OTTENUTI PER COLATA

Per avere Hc elevato bisogna ostacolare il libero movimento dei domini ad es. con trattamento di tempra. sono disponibili i seguenti materiali (Tab. 21.1):

acciai martensitici che sono stati i primi materiali disponibili.

leghe ALNI e ALNICO;

le leghe ALNI sono leghe di Fe con Ni ed Al.

le leghe ALNICO sono leghe di Fe con Ni, Al (O Ti) e Co.

Sia le leghe ALNI che le leghe ALNICO possono essere tensionate internamente con raffreddamenti rapidi.

 

Tab. 21.1 - Caratteristiche di materiali per magneti permanenti ottenuti per colata.

MATERIALI OTTENUTI PER SINTERIZZAZIONE

Sono ancora i materiali tipo ALNI ed ALNICO che, per diminuire i costi, possono essere ottenuti con processi di sinterizzazione partendo dal materiale in polvere. Si ha un leggero decadimento delle caratteristiche. si usano anche con ottimi risultati leghe sinterizzate di ferro con altri elementi e di cobalto con terre rare:

Lega al samario - cobalto (Sm2Co17).

Lega di ferro, neodimio e boro.

si può ottenere un materiale anisotropo pressando le polveri sotto l’azione di un campo magnetico. appartengono a questi tipi l’ALNICO 5 che può essere ottenuto con magnetizzazione direzionale e con cristalli orientati.

 

Tab. 21.2 - Caratteristiche di materiali sinterizzati.

MATERIALI CERAMICI OTTENUTI DA POLVERI FINISSIME

Si può ridurre un materiale per magneti permanenti in granuli della dimensione di un dominio. si ha magnetizzazione solo per spostamento delle pareti. Citiamo come esempio la ferrite di bario che presenta le seguenti caratteristiche:

Hc = 120.000 As/m            Bs = 0,20 T          (HB)MAX = 6.000

 

Tutti i materiali usati per produrre magneti permanenti sono duri e molto fragili. non possono quindi essere sottoposti a lavorazioni per asportazione di truciolo.

RIEPILOGO DELLA LEZIONE 3.8

Sono state richiamate le relazioni che descrivono i magneti permanenti.

Sono stati introdotti il prodotto di energia e la retta di ritorno.

Sono stati descritti i principali materiali usati per i magneti permanenti.

RIEPILOGO DELLA 3a PARTE

Sono stati richiamati i principi relativi al comportamento magnetico dei materiali.

Sono stati descritti i materiali  ferromagnetici  e ferrimagnetici.

 

Fonte: http://unina.stidue.net/Universita'%20di%20Trieste/Ingegneria%20Industriale%20e%20dell'Informazione/Contin/Costruzioni_elettromeccaniche/MAGNETB.DOC

Sito web da visitare: http://unina.stidue.net

Autore del testo: non indicato nel documento di origine

Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.

 

Materiali ferromagnetici

 

 

I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

Materiali ferromagnetici

 

"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco

www.riassuntini.com dove ritrovare l'informazione quando questa serve