Modulo elastico E dei materiali

provocano un orientamento preferenziale dei grani cristallini. I materiali compositi sono spesso volutamente anisotropi, grazie alle differenti proprietà meccaniche di matrice e fibre.
In tab.1 sono riassunte le principali caratteristiche delle varie categorie di materiali.

Proprietà fisiche di interesse

Vengono di seguito riassunte le proprietà fisiche di interesse per i materiali da costruzione. Alcune di esse sono approfondite nei paragrafi successivi, mentre il comportamento in campo plastico e la resistenza a frattura e a fatica sono trattate in capitoli specifici. Nella tab.2 sono riassunte alcune delle proprietà fisiche di maggiore interesse di vari materiali da costruzione.

Proprietà meccaniche

Descrivono il comportamento del materiale assoggettato a forze statiche o dinamiche:

• comportamento sforzi-deformazioni (elastico, plastico, viscoelastico) e resistenza statica (tipicamente quantificata mediante le tensioni di snervamento e rottura),
• comportamento sforzi-deformazioni e resistenza statica ad alta temperatura,
• resistenza all’indentazione, alla scalfittura e all’abrasione (durezza),
• resistenza agli urti (resilienza),
• resistenza a frattura (tenacità a frattura),
• resistenza a fatica.

Proprietà termiche

Descrivono il comportamento del materiale assoggettato a variazioni di temperatura:

• dilatazione termica,
• capacità termica,
• conduttività termica,
• resistenza allo shock termico.

Temperatura di fusione

La temperatura di fusione Tf è la temperatura alla quale il materiale passa dallo stato solido a quello liquido. Ovviamente le temperature di esercizio dei componenti meccanici devono essere convenientemente minori di essa. Per i polimeri è altrettanto importante la temperatura di transizione vetrosa Tg, che è la temperatura al  di sotto della quale i polimeri diventano rigidi e fragili come il vetro. Le plastiche rigide hanno Tg di circa 100°C. Le plastiche flessibili e gli elastomeri gommosi hanno Tg inferiori alla temperatura ambiente.

Densità

La densità r è definita come rapporto tra la massa del materiale e il volume occupato, tipicamente espressa in g/cm3. Nei casi in cui il peso di un componente ha rilevanza, si può parlare di resistenza specifica del  materiale, intendendo il rapporto tra la grandezza che identifica la resistenza e la densità (ad esempio la resistenza specifica a rottura è il rapporto tra la tensione di rottura e la densità).

Proprietà elettriche

La principale proprietà elettrica di interesse dei materiali da costruzione è la conduttività (o il suo opposto, la resistività), che è l’attitudine a trasmettere la corrente elettrica.

Proprietà tecnologiche

Le proprietà tecnologiche descrivono l’attitudine di un materiale ad essere lavorato per produrre dei manufatti o ad essere trattato per acquisire determinate proprietà.

Duttilità/Malleabilità

Queste proprietà si riferiscono all’attitudine di un materiale ad essere lavorato a freddo per deformazione plastica. La duttilità e la malleabilità si riferiscono rispettivamente all’attitudine del materiale ad essere ridotto in fili mediante trazione e in lamine mediante compressione.

Fusibilità

È l'attitudine di un materiale a passare dallo stato solido allo stato liquido mediante riscaldamento, per  essere poi raffreddato in modo da assumere la forma desiderata. La fusibilità di un materiale cresce al diminuire della temperatura di fusione.

Saldabilità

È l'attitudine di un materiale ad essere saldato, cioè la proprietà in base alla quale pezzi del materiale possono essere uniti ad altri pezzi dello stesso o di altri materiali, se portati a temperature prossime (ma inferiori) al loro punto di fusione.

Temprabilità

È l'attitudine di un materiale ad acquistare maggiore durezza e resistenza meccanica attraverso il processo di tempra, costituito da un riscaldamento a temperatura elevata, ma minore di quella di fusione, e un successivo raffreddamento brusco.

Tab.10.1 - Tabella riassuntiva di alcune caratteristiche delle principali categorie di materiali.

Tab.10.2 - Alcune proprietà dei materiali da costruzione ben rappresentative della rigidezza, della resistenza e della possibilità di impiego ad alta temperatura: il modulo di Young E, la tensione di rottura sr, la densità r, la temperatura di fusione Tf e il coefficiente di Poisson n.

Comportamento sforzi/deformazioni - Prova di trazione

Il comportamento del materiale per ciò che concerne il rapporto tra le tensioni cui è soggetto e le deformazioni che si destano è definito:

• lineare se la deformazione è direttamente proporzionale alla tensione applicata,
• elastico se le deformazioni si annullano al cessare delle tensioni applicate,
• plastico se rimangono deformazioni permanenti al cessare delle tensioni applicate.

La deformazione elastica è legata allo stiramento dei legami interatomici nei solidi che cessa al cessare delle tensioni, mentre la deformazione plastica è legata allo slittamento tra piani di atomi nei grani cristallini che accade  in modo incrementale a causa del movimento delle dislocazioni sotto tensioni elevate. Per questa natura fisica, la deformazione plastica non provoca variazioni di volume nel materiale.
Il comportamento sforzi-deformazioni di un materiale è generalmente caratterizzato mediante la prova di trazione.
Essa consiste nel sottoporre un provino di geometria e dimensioni opportune (solitamente standardizzate da norme tipo ISO o ASTM) ad una forza di trazione unidirezionale F crescente lentamente da 0 ad un valore tale da determinarne la rottura, misurando la forza applicata e la deformazione in uno dei modi che verrà descritto nel seguito. Usualmente il provino è una barretta a sezione costante circolare (con diametro iniziale d0) o rettangolare di area iniziale A0. In molti casi esso è conformato in modo di avere delle estremità più robuste da afferrare ed una porzione più sottile che costituisce  il tratto utile per la prova di lunghezza L0.
Il provino viene collegato ad una macchina di prova (fig.1)
dalle estremità, mediante afferraggi, uno dei quali è fisso, e l’altro è solidale alla traversa mobile della macchina (o al pistone attuatore). Lo spostamento di quest’ultima permette l’applicazione del carico. La distanza tra gli afferraggi è indicata con h.
Durante la prova si misurano la forza applicata mediante un apposito trasduttore (cella di carico) e lo spostamento dell’elemento mobile Dh (mediante un dispositivo detto Linear Variable Differential Transformer o LVDT). In molti casi si misura l’allungamento localizzato su un piccolo tratto del provino mediante un estensometro o direttamente la deformazione un estensimetro; la lunghezza del tratto su cui si effettua la misura è pari alla base di misura del trasduttore stesso.
I  dati  misurati  sono  riportati  su  un  diagramma tensioni
nominali-deformazioni nominali (s-e), nel quale le prime sono

date dal rapporto tra il carico applicato e l'area iniziale del provino

Fig.10.1 - Macchina di prova servoidraulica.

o  = Fi
A0

(10.1)

e sono misurate in MPa, le seconde dal rapporto tra l’allungamento totale e la lunghezza iniziale:
e = L - L0   = DL

(10.2)

L0                 L0
e sono adimensionali. In alcuni casi può essere conveniente esprimere le deformazioni in percentuale: in questo caso basta moltiplicare il valore misurato con la (2) per 100 e aggiungere il simbolo % (ad es. e=0.1 corrisponde ad una deformazione del 10%). Nelle misure effettuate con gli estensimetri, per comodità, si misurano le deformazioni in micrometri per metro mm/m; in questo caso basta moltiplicare il valore misurato con la (2) per 1.000.000 (essendo 1mm=1m/1.000.000).
In alcuni casi l’allungamento DL viene stimato dallo spostamento dell’attuatore, semplicemente come DL= Dh. In generale questo valore coincide con l’allungamento medio del tratto del provino compreso tra gli afferraggi, che coincide con l’allungamento locale solo in campo elastico. Poiché il valore medio è influenzato dalla lunghezza iniziale L0, essa è standardizzata e tipicamente si ha L0=5d0. Se si utilizza l’estensometro, il valore L0 coincide con la base di misura dello stesso: il vantaggio è che il valor medio è calcolato su un tratto ridotto ed è più vicino al valore locale. Per materiali di elevata rigidezza si verifica spesso uno slittamento del provino negli afferraggi e  l’utilizzazione dell’estensometro/estensimetro diventa necessaria.
Si deve notare che la tensione nominale non coincide con quella realmente agente, poiché, come si vedrà nel seguito, la sezione del provino scarico A0  é maggiore di quella che si ha durante l’applicazione della tensione per   via

• Tensione massima             

B

A Limite di proporzionalità   

s
A    Tensione di snervamento
ss

•  C

B
C¢
A

s

sp                  A

e                                                  e                                               e                                            e
O          B
(a)                                                           (b)                                          (c)                                                 (d)
Fig.10.2 - Diagramma s-e: (a) materiale duttile; (b) materiale fragile; (c) limiti di proporzionalità (A), elastico (B) e di snervamento (C) e (C’);
(d) energia elastica totale.
dell’effetto Poisson; questa differenza è trascurabile fino a quando il materiale si mantiene in campo elastico. Si deve notare, inoltre, che la deformazione nominale, in dipendenza dal modo con cui è misurato DL, è data dalla deformazione media rispetto alla base di misura dell'estensimetro. Le tensioni e deformazioni nominali riportate nel diagramma sono dette anche ingegneristiche.
Le prove possono essere condotte imponendo che la traversa della macchina si muova con velocità dh/dt costante (controllo di spostamento) oppure che la deformazione applicata cresca con velocità de/dt costante (controllo di deformazione). In alternativa si impone che il carico cresca con velocità dF/dt costante (controllo di carico).
Il primo caso è quello più frequente e la velocità di spostamento della traversa (o del pistone) è spesso imposta dalle normative.
Una prima osservazione del diagramma permette di distinguere due categorie di materiali: i duttili (fig.2a), che giungono a rottura con ampi valori di deformazione (acciai, alcuni polimeri ecc...) e i fragili (fig.2b), che giungono a rottura con valori di deformazione limitati (ghise, materiali ceramici, alcuni polimeri).

Modulo di Young-Coefficiente di Poisson-Limite di proporzionalità

Il primo tratto del grafico s-e è spesso approssimabile ad una retta: in questo caso il materiale presenta un comportamento detto lineare-elastico nel quale le deformazioni misurate sono direttamente proporzionali alle tensioni agenti e le deformazioni si annullano al cessare del carico. Il rapporto fra tensione applicata e deformazione è una costante tipica del materiale che prende il nome di modulo di Young

espresso in MegaPascal. Se si diminuisce il carico il punto rappresentativo sul diagramma s-e ripercorre il tracciato a ritroso sino all’origine degli assi evidenziando l’assenza di deformazioni residue. Per una maggiore precisione è opportuno che E sia valutato considerando il rapporto tra le differenze tra tensioni e deformazioni misurate in due  punti distanti sul tratto rettilineo del grafico s-e, evitando i punti troppo vicini all’origine degli assi e al valore di snervamento (ad es. i punti con tensione pari al 10% e al 50% della tensione massima della prova). Una stima più precisa può essere ottenuta effettuando una regressione lineare su tutti i valori del tratto lineare compresi tra due punti opportuni.
In altri casi non vi è una regione lineare ben definita e il concetto di modulo di Young deve essere considerato con cautela. In alcuni casi si considera il coefficiente angolare della retta tangente alla curva s-e nell’origine.
Come è noto, sempre in campo elastico, applicando una tensione monoassiale longitudinale, oltre alla deformazione longitudinale imposta, si verifica una contrazione trasversale ad essa proporzionale, misurabile dalla variazione del diametro del provino. La costante di proporzionalità tra le deformazioni è il coefficiente di Poisson (valore positivo) che può essere valutato misurando la deformazione trasversale e utilizzando la relazione

Le costanti E e n sono definite costanti ingegneristiche, in quanto direttamente ricavabili dalle prove meccaniche.
Ad un certo valore della tensione detto limite di proporzionalità sp la curva s-e comincia a deviare dalla linea retta come nel punto A delle figg.2a e 2c; oltre questo valore il materiale può essere ancora elastico, ma non obbedisce più alla legge lineare di Hooke. Per molti materiali é possibile aumentare la tensione oltre il limite di proporzionalità sino a un valore di tensione detto limite elastico (punto B di fig.2c) senza che si abbiano deformazioni residue permanenti (misurabili, cioè, quando il carico viene riportato a zero). È difficile ottenere questo valore dai diagrammi di trazione, in quanto sarebbe necessario che il provino venisse scaricato di volta in volta per misurare la deformazione residua.

Tensione di snervamento-Tensione di rottura

Per molti materiali si nota un valore di tensione in corrispondenza del quale la deformazione comincia ad aumentare molto rapidamente senza un equivalente incremento di tensione. Tale tensione é definita tensione di snervamento ss (punto C in fig.2c) e caratterizza il passaggio del materiale dallo stato elastico a quello plastico. Le deformazioni plastiche sono permanenti: all’azzeramento del carico il comportamento del materiale è descritto da una retta parallela a quella relativa al comportamento elastico con pendenza pari al modulo di Young (fig.2c). Tale retta,

Come già detto la tensione reale risulta generalmente maggiore di quella nominale poiché generalmente è A<A0 a causa della strizione. Sperimentalmente si osserva, inoltre, che la tensione reale cresce sempre durante la prova.
Come visto precedentemente, le deformazioni nominali sono valori medi rispetto alla lunghezza di riferimento e, per la loro valutazione, l’allungamento complessivo DL viene riferito alla lunghezza iniziale L0. In realtà l’allungamento complessivo DL può essere visto come la somma di incrementi istantanei di lunghezza dLi ciascuno dei quali avviene mentre il provino ha lunghezza istantanea Li maggiore di quella iniziale. La deformazione reale istantanea è data dal rapporto dLi/Li e la deformazione totale all’istante iesimo è data dall’integrale di tale rapporto tra la configurazione iniziale e quella nell’istante considerato

Introducendo L=L0+DL nella (6), si può mostrare che sussiste la seguente relazione:
e R = ln (e +1)

In campo elastico le tensioni e deformazioni reali risultano praticamente coincidenti, mentre in campo plastico le deformazioni reali ottenute dalla (7) sono inferiori a quelle nominali. E’ bene notare che la (7) è utilizzabile solo in assenza di strizione, perché nella definizione di deformazioni reali (6) devono essere introdotti gli allungamenti locali della sola zona soggetta a deformazione e non quelli relativi a tutta la lunghezza utile del provino o alla base  di misura dell’estensometro. Per questo motivo, a dispetto della (7), le deformazioni reali nei materiali duttili risultano maggiori di quelle nominali.
Poiché gli allungamenti reali nella zona deformata sono difficili da misurare è spesso necessario sfruttare la costanza del volume del materiale in campo plastico. Trascurando le modeste variazioni di volume dovute alla deformazione elastica, la costanza del volume del provino può essere espressa dalla seguente relazione
A0 L0=A L                                                                                                                                   (10.8)
dalla quale è possibile ricavare l’espressione della area della sezione istantanea del provino:

A=A0 L0/L                                                                 (10.9)
Utilizzando queste espressioni è possibile scrivere le seguenti relazioni tra tensioni e deformazioni nominali e reali:

Altre proprietà deducibili dalla prova di trazione: Duttilità/Malleabilità - Resilienza - Tenacità Duttilità/Malleabilità

La duttilità è la capacità di un materiale di assorbire deformazioni anelastiche senza rompersi. A parità di resistenza e durezza, i materiali più duttili sono più adatti ad assorbire sovraccarichi e ad essere lavorati a freddo per deformazione plastica.
La duttilità viene quantificata mediante la deformazione al momento della rottura:

ottenuta sul diagramma s-e, o mediante l’allungamento percentuale=100 er.
Usualmente si ammette che al di sotto del 5% di allungamento il materiale sia fragile, al di sopra duttile (fig.2a,b). Per una valutazione più realistica della duttilità, l'allungamento del materiale può essere misurata con un  estensometro.
Una misura alternativa della duttilità è data dalla riduzione percentuale della sezione, chiamata %RA:

L’analoga grandezza misurata mediante una prova di compressione viene definita malleabilità; i materiali malleabili sono adatti ad essere lavorati per deformazione plastica per ottenere lastre.

Resilienza – Tenacità a trazione

L’energia totale di deformazione immagazzinata nel volume V del provino nell’istante i di prova (pari al lavoro compiuto dalla forza applicata) è data dalla seguente espressione:

In campo elastico esso è pari al lavoro compiuto dalla forza applicata sul provino, mentre in campo plastico una grande quantità di questo lavoro è dissipato in forma di calore.
La resilienza è la capacità di assorbire energia nel campo elastico. Il modulo di resilienza è l'energia di deformazione ad unità di volume immagazzinata nel materiale quando la tensione è al limite di proporzionalità; ponendo V=1, s=sp e considerando che in campo elastico ep=sp/E si ottiene:

In fig.2d il punto A rappresenta la sp e l'area tratteggiata rappresenta l’energia Ures. La resilienza risulta elevata per alti valori della sp e bassi valori di E.
La tenacità a trazione (da non confondere con la tenacità a frattura) è la capacità di assorbire energia prima della rottura. Essa si quantifica misurando l’energia di deformazione totale alla rottura rappresentata da tutta l’area sottesa dalla curva s-e.
Se la curva s-e è tendenzialmente piatta dopo il valore di snervamento, come accade per i materiali duttili, una buona approssimazione dell’energia è data da questa espressione:
o s  + s r

In materiali fragili per quali la curva s-e ha un andamento parabolico si può utilizzare la seguente espressione

Prova di Compressione

Vari materiali impiegati nella costruzione di elementi meccanici hanno proprietà differenti se sottoposti a trazione o a compressione. Tipicamente i materiali fragili hanno un carico di rottura a compressione nettamente superiore a quello di trazione. Si deve ricordare che le tensioni di trazione tendono a fare propagare le discontinuità nel materiale (fratture, difetti) mentre quelle di compressione tendono a chiuderle.
I provini di compressione hanno geometrie diverse da quelli di trazione, infatti, se il provino é troppo lungo si può

indurre una flessione spuria o si può verificare un caso d’instabilità, se é corto, l'attrito alle estremità può rendere lo stato di tensione più complesso di quello monoassiale necessario per la determinazione della curva sforzi- deformazioni. Il compromesso migliore si raggiunge con provini cilindrici con rapporto l/d»3.
Nel caso di materiali duttili la tensione di rottura in compressione non può essere determinata poiché nella regione plastica l'incremento della superficie diminuisce notevolmente la tensione agente a parità di carico applicato. Ancora, all'aumentare del carico il materiale si schiaccia e tende a ridursi ad un disco piatto; in definitiva, a differenza della trazione, non vi é un valore di tensione ben definito nel quale si ha una variazione di sezione. I risultati delle prove sono rappresentati da un diagramma tensione-deformazione in modo simile alle prove di trazione. Le prove di trazione e compressione devono essere eseguite separatamente, diversamente si assume che il materiale ha la stessa resistenza nei due casi.

Prova di flessione

La prova di flessione permette di determinare il modulo di Young e stimare la tensione di rottura di materiali fragili; tale tensione deve essere indicata come tensione di rottura a flessione srf. Nella prova a tre punti i provini vengono vincolati con due appoggi nella parte inferiore e caricati al centro da un cuneo solidale alla traversa mobile della macchina. Nella prova a quattro punti la traversa mobile spinge due cunei disposti simmetricamente rispetto alla mezzeria del provino. Nel corso della prova si misurano lo spostamento della traversa Y, coincidente con la freccia in mezzeria, e il carico applicato F.
La prova di flessione presenta i seguenti vantaggi:

• semplicità d’afferraggio ed esecuzione,
• semplice geometria del provino generalmente a sezione rettangolare,
• spostamenti ampi di misurazione più precisa.

Poiché la tensione varia linearmente lungo lo spessore, lo snervamento viene raggiunto inizialmente solo in un sottile strato superficiale; superato il

campo elastico, inoltre, gli spostamenti misurati non possono essere utilizzati per calcolare le deformazioni e l’unica informazione utile è la forza a rottura Fr. La prova di flessione risulta, quindi, poco sensibile per la determinazione dell’inizio dello snervamento ed è adatta alla caratterizzazione di materiali fragili con comportamento lineare.
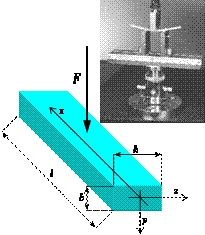
La geometria del provino (fig.3) è descritta dai seguenti parametri:

• l=lunghezza utile (la parte tra gli appoggi),
• b=larghezza della sezione,
• h=altezza della sezione.

La tensione massima agisce in mezzeria sulla superficie del lato teso (x=l/2, y=h/2). Nel caso di flessione a tre punti essa può essere espressa mediante la formula di Navier
Introducendo Fr nella (18) si ottiene la tensione di rottura a flessione del materiale.
La deformazione massima, a sua volta, può essere espressa in funzione della freccia nel seguente modo (vedi appendice)

In teoria il modulo di Young potrebbe essere valutato con una qualsiasi coppia di valori F, Y misurati in campo elastico
Una migliore precisione può essere ottenuta utilizzando due punti sperimentali

(10.21)

Le (20) e (21) possono essere riscritte utilizzando la pendenza K della retta F(Y) che descrive l’andamento del carico in funzione della freccia in campo elastico

Questa relazione permette di calcolare E nel caso in cui K può essere stimato dai dati sperimentali F-Y nella zona lineare, ad esempio mediante una regressione lineare.

Prove di Durezza

La durezza è l’attitudine degli strati superficiali di un materiale a resistere all’indentazione (creazione di una impronta sulla superficie), alla scalfittura, all’abrasione e alla deformazione per compressione.
La durezza si determina creando un’impronta sulla superficie del materiale mediante un elemento penetratore (indentatore), che viene pressato ortogonalmente alla superficie in modo statico con un valore di carico F prefissato, e misurando una dimensione caratteristica dell’impronta stessa. Esistono vari metodi (Brinell, Rockwell, Vickers e Knopp) che si differenziano per la forma del penetratore e per il modo di misurare l’impronta. Le prove di durezza non sono distruttive e possono essere eseguite direttamente sul componente.