I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
L'algebra è una branca della matematica che studia le strutture algebriche, cioè quegli insiemi di sostegno muniti di operazioni in cui gli operandi sono espressi sia con numeri che con lettere.
Le origini dell’algebra risalgono al noto matematico persiano Muhammad ibn Musa al-Khwarizmi, e precisamente il termine algebra è preso dal titolo del suo libro Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala in cui tratta la risoluzione delle equazioni di primo e di secondo grado.
Il più semplice tipo di algebra è appunto l’algebra elementare, che rappresenta un’evoluzione ai principi base dell'aritmetica, dove oltre ai numeri e le quattro operazioni aritmetiche, compaiono anche simboli.
In tutte le discipline scientifiche l’algebra è molto utilizzata, in quanto consente la formulazione delle relazioni funzionali. Ad esempio in fisica classica, la maggior parte delle relazioni che descrivono i fenomeni naturali sono espresse mediante formulazioni algebriche.
In questo argomento, tratteremo in particolare le proprietà e i metodi di risoluzione delle operazioni in cui compaiono operandi costituiti da numeri e lettere, al fine di poter risolvere espressioni letterali.
«
Proprietà delle potenze
Prima di procedere è utile introdurre il concetto di variabile. Il termine variabile indica un oggetto, una lettera o un qualsiasi simbolo che può assumere valori diversi, appartenenti ad un certo insieme, in momenti diversi. Ad esempio, se consideriamo la formula per calcolare l’area di un rettangolo,
, dove 
è l’area del rettangolo, 
la base ed 
l’altezza, è facile intuire che le variabili 
e 
assumeranno valori diversi per rettangoli diversi.
Di seguito un breve schema che illustra le proprietà delle potenze in cui sono presenti le lettere, le quali possono essere sostituite con qualsiasi numero.
Condizione importante!
Se in un’espressione letterale, una lettera compare più volte, in ogni momento a lettera uguale corrisponde numero uguale.
Ricordiamo che la potenza è l’operazione in cui si moltiplicano più volte numeri uguali:
E di seguito vediamo le principali proprietà delle potenze:
La potenza di un prodotto è il prodotto delle singole potenze:
(2.1)
La potenza di una frazione è la frazione delle singole potenze:
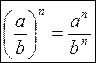(2.2)
Ogni potenza ad esponente unitario corrisponde alla sua stessa base:
(2.3)
In pratica, il numero 1 è l’elemento neutro della potenza.
Ogni potenza con base diversa da zero, ad esponente nullo corrisponde ad 1:
(2.4)
Ogni potenza con esponente negativo corrisponde al reciproco della potenza ad esponente positivo:
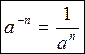(2.5a) 
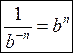(2.5b) 
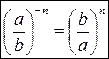(2.5c)
Dalla definizione di potenza e da queste prime cinque proprietà, si ricavano tutte le proprietà descritte in seguito.
Il prodotto di potenze aventi la stessa base, è una potenza che per base ha la stessa base e per esponente la somma degli esponenti degli operandi:
(2.6)
Esempio: 
Dimostrazione:
La divisione, o frazione di potenze aventi la stessa base, è una potenza che per base ha la stessa base e per esponente la differenza degli esponenti degli operandi.
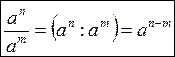(2.7)
Esempio: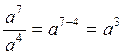 
Dimostrazione:
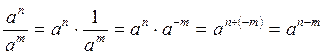
La divisione, o frazione di potenze aventi la stessa base, è una potenza che per base ha la stessa base e per esponente il prodotto degli esponenti degli operandi.
(2.8)
Esempio: 
Dimostrazione:
«
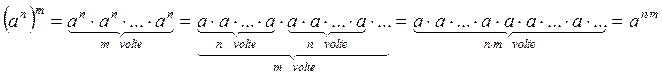
Sommatoria, produttoria e fattoriale
Un altro richiamo importante è quello del concetto di funzione che è stato descritto nell’argomento-1 di quest’opera.
Def. Dati due insiemi non vuoti, 
e 
, la funzione (o applicazione) tra l’insieme 
e l’insieme 
che si indica con la scrittura 
è una legge che associa ad ogni elemento di 
uno e un solo elemento di 
(corrispondenza univoca).
Per la spiegazione, approfondire l’argomento attraverso il paragrafo “Cenni di Funzioni” dell’argomento-1.
In sostanza, a partire da un insieme 
, attraverso una legge 
, otteniamo come risultato un insieme 
(sottoinsieme di 
) contente gli elementi di 
che sono associati agli elementi dell’insieme 
.
Dato un insieme 
, costituito da una sequenza di numeri che va da 1 a 
, con il valore di 
noto, e data una legge 
, possiamo definire:
;
.
Generalmente, nella sommatoria e nella produttoria, la variabile indipendente si indica con la lettera 
. Il simbolo utilizzato per indicare la sommatoria è 
(sigma maiuscolo), e la sua operazione si scrive 
.
Attraverso questa scrittura, possiamo dire che l’insieme 
è costituito dagli elementi 
, mentre l’insieme 
, per la legge 
, è costituito dagli elementi associati 
. Il risultato della sommatoria è un numero dato dalla somma degli elementi dell’insieme 
. Pertanto possiamo scrivere:
(3.1)
Ad esempio proviamo a calcolare il risultato della sommatoria 
:
L’insieme 
è costituito dagli elementi 
, mentre l’insieme 
, per la legge 
, è costituito dai quadrati degli elementi di 
, per cui 
.
Quindi 
.
Non necessariamente la sequenza deve partire da 1, basta indicare sotto al simbolo di sommatoria, invece di 
, ad esempio la scrittura 
se si vuole partire da 2 oppure 
se si vuole partire da 3 e così via.
Altro esempio, proviamo a calcolare 
L’insieme 
è costituito dagli elementi 
, mentre l’insieme 
, per la legge 
, è costituito degli elementi di 
moltiplicati per 3 e sottratti di una unità, per cui 
, poiché 
, 
e 
.
Quindi 
.
Il simbolo utilizzato per indicare la produttoria è 
(pi maiuscolo), e la sua operazione si scrive 
. Il procedimento è analogo a quello della sommatoria, cambia il calcolo del risultato, che invece della somma è il prodotto degli elementi dell’insieme 
.
(3.2)
Ogni ulteriore spiegazione sarebbe superflua, pertanto passiamo direttamente agli esempi.
Esempio, proviamo a calcolare 
L’insieme 
è costituito dagli elementi 
, mentre l’insieme 
, è costituito degli elementi di 
moltiplicati per 2 e sommati di una unità, per cui 
.
Quindi 
.
Il fattoriale di un numero 
, si scrive 
e si legge “n fattoriale” o “fattoriale di n”, corrisponde al prodotto dei numeri che vanno da 1 a 
.
(3.3)
Ad esempio 
.
Di seguito riportiamo il fattoriale dei primi 10 numeri naturali:
Da questo elenco è facile notare che il valore del fattoriale cresce molto rapidamente.
Una proprietà fondamentale è la sua scomposizione:
(3.4)
Cioè il fattoriale di un numero corrisponde al fattoriale del precedente per il numero stesso, ad esempio 
corrisponde al fattoriale di 3 moltiplicato per 4. Possiamo scrivere quindi 
, infatti 
e 
.
Grazie a questa proprietà, siamo anche in grado di stabilire che il fattoriale di 0 è uguale a 1.
(3.5)
Dimostrazione:
Per la proprietà anzidetta 
. Essendo 
e 
, per la proprietà transitiva anche 
.
«
Coefficiente binomiale
Il coefficiente binomiale, che riprenderemo nel calcolo combinatorio nelle prossime lezioni, è un’importante applicazione del fattoriale, in grado di calcolare le combinazioni semplici senza ripetizione.
Esempi di combinazione semplice senza ripetizione li ritroviamo spesso nella nostra vita quotidiana, ad esempio quando calcoliamo le probabilità di vincere al lotto.
Con il coefficiente binomiale possiamo calcolare ad esempio quanti terni ci sono in cinque numeri, oppure quante sono le combinazioni del superenalotto, o ancora quante coppie posso formare con un certo numero di persone e così via.
Come abbiamo detto prima, il coefficiente binomiale è un’applicazione del fattoriale, ci sono due variabili che indicheremo con 
e 
, si scrive 
ed è dato dalla seguente formula:
(4.1)
Esempio 1: 
Esempio 2: 
In pratica, la scrittura 
, calcola quante combinazioni di 
numeri (senza ripetizioni) si formano utilizzando 
numeri.
Per introdurci nel cuore del concetto, partiamo con un esempio molto semplice. Proviamo a rispondere a questa domanda: “Quante coppie (due persone) si possono fare con 3 persone?”.
Indichiamo le tre persone con A, B e C. Le possibili coppie sono AB, AC e BC, quindi le coppie sono 3. Confrontiamo adesso questo risultato con quello calcolato attraverso il coefficiente binomiale.
In questo caso 
vale 3 poiché le persone sono 3, mentre 
vale 2 poiché le coppie sono formate da 2 persone.
Il risultato è 3, proprio il numero delle possibili coppie.
Procediamo con qualcosa di leggermente più complicato. Ora la domanda è “Quanti terni si possono fare con 5 numeri?”
In questo caso 
vale 5 e 
vale 3, poiché vogliamo calcolare le combinazioni di 3 numeri (senza ripetizioni) su 5.
Abbiamo così calcolato che su 5 numeri ci sono ben 10 terni.
Infine, proviamo a calcolare le combinazioni del superenalotto. In pratica, dobbiamo calcolare quante sestine (combinazioni di 6 numeri) si possono fare con 90 numeri. In questo caso 
vale 90 e 
vale 6, poiché vogliamo calcolare le combinazioni di 6 numeri (senza ripetizioni) su 90.
Facciamo qualche riflessione sul calcolo. Il fattoriale di 90 è un numero composto da 139 cifre, e questo rende il calcolo molto complesso. Possiamo renderlo molto più semplice utilizzano le proprietà del fattoriale.
Sfruttando la proprietà del fattoriale (3.4) possiamo scrivere:
Sostituiamo il fattoriale di 90 nel calcolo delle combinazioni:
A questo punto, possiamo semplificare il fattoriale di 84 e calcolare le combinazioni con numeri più gestibili.
…. Forse questo risultato ci suggerisce qualcosa ….
Il nome “coefficiente binomiale” nasce dal calcolo della potenza di binomio (binomio di Newton) che vedremo più avanti in questa lezione, nel paragrafo delle operazioni con i polinomi.
Monomi e sue operazioni
Un monomio è un’espressione algebrica che esprime una quantità, ed è costituito da tre parti:
Un esempio di monomio è 
, dove, in questo caso il segno è “─”, il coefficiente (parte numerica) è il “
” e la parte letterale è “
”.
Vale la pena spendere qualche parola su tutto ciò che può essere sottinteso.
Quando non è specificato il segno, si sottintende che tale segno sia positivo, ad esempio per il monomio 
è sottinteso che si tratta di 
.
Quando non è specificata la parte numerica, si sottintende che tale coefficiente sia il numero 1. Ad esempio per il monomio 
è sottinteso che si tratta di 
. Questo perché il numero 1 è l’elemento neutro della moltiplicazione, ed essendo il monomio sostanzialmente una moltiplicazione tra le parti, è possibile applicare questa proprietà. Infatti, se 
per tale proprietà, vale anche l’uguaglianza 
.
Quando ad una lettera non è specificato l’esponente, per la proprietà (2.3) delle potenze, si sottintende che tale esponente sia il numero 1. Ad esempio per il monomio 
è sottinteso che si tratta di 
.
Quando in una parte letterale non è specificata una lettera, possiamo eventualmente sottintendere che questa lettera ci sia con esponente nullo. Infatti, combinando la proprietà dell’elemento neutro della moltiplicazione con la proprietà (2.4) delle potenze, possiamo sottintendere la presenza di altre lettere nella parte letterale.
Ad esempio consideriamo il monomio 
.
.
.
Infine, per queste 2 proprietà 
.
Inoltre, un monomio può essere considerato tale anche se mancante della parte letterale.
Passiamo adesso alle definizioni più importanti:
Due monomi si dicono simili quando hanno la stessa parte letterale. Ad esempio, i monomi 
e 
sono simili, infatti, hanno la parte letterale (
) in comune.
Dobbiamo distinguere due tipi di grado:
Il grado complessivo è la somma di tutti chi esponenti delle lettere presenti nella parte letterale, mentre il grado rispetto ad una lettera corrisponde all’esponente della lettera a cui si fa riferimento.
Esempio 1: 
Grado complessivo: 
Grado rispetto alla 
: 
Grado rispetto alla 
: 
Grado rispetto alla 
: 
Esempio 2: 
Grado complessivo: 
Vediamo adesso le operazioni.
L’addizione o la sottrazione algebrica fra monomi può avvenire solo quando gli addendi sono tra loro simili, cioè che posseggono la stessa parte letterale. La somma o la differenza algebrica è anch’essa un monomio che ha la stessa parte letterale dei suoi operandi e come coefficiente la somma o la differenza algebrica dei coefficienti degli operandi. Ad esempio 
.
Parte letterale: 
Operazione algebrica: 
Quindi 
Per l’addizione e la sottrazione algebrica fra monomi valgono tutte le proprietà dell’addizione e della sottrazione aritmetica descritte nell’argomento-2.
Il prodotto tra due o più monomi è quel monomio che ha:
Ad esempio, eseguiamo la seguente moltiplicazione:
: 
: 
: 
Quindi, 
Il quoziente tra due monomi è quel monomio che ha:
Ad esempio, eseguiamo la seguente divisione: 
: 
: 
: 
Quindi, 
L’elevamento a potenza di un monomio produce come risultato quel monomio che ha:
Per la potenza del segno, ricordiamo che il segno positivo rimane positivo per qualsiasi potenza, mentre il segno negativo rimane negativo per le potenze dispari e diventa positivo per potenze pari.
Regola della potenza del segno: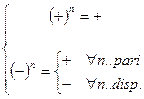 
Ad esempio, eseguiamo la seguente potenza: 
: 
: 
: 
Quindi, 
Il massimo comune divisore (M.C.D.) e il minimo comune multiplo (m.c.m.) di due o più monomi è un monomio che va calcolato come segue:
Per la parte numerica, il massimo comune divisore e il minimo comune multiplo seguono le regole descritte nell’argomento-2.
Per la parte letterale invece seguiamo le due semplici regole seguenti:
Fonte: http://www.atuttoportale.it/didattica/a_scuola_di_matematica/argomento-03.doc
Sito web da visitare: http://www.atuttoportale.it/
Autore del testo: indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve