Equazioni

 

 

 

I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore

 

 

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

 

 

 

Equazioni

 

Le Equazioni algebriche

1 Introduzione

Nella maggior parte dei casi, le equazioni vengono proposte subito dopo il calcolo letterale senza un esplicito collegamento con i problemi. Gli studenti vedono quindi tale argomento come svincolato da contesti reali e da studiare per il semplice fatto che fa parte del programma scolastico. Credo che sia preferibile adottare subito un approccio per problemi, perché introducendo ogni nuovo concetto, costruzione o procedimento dopo aver in qualche modo esplorato ciò che è già stato acquisito (si può proporre un problema, difficilmente risolubile senza un metodo algebrico per esempio), e preso coscienza della necessità di procedere oltre, a causa della constatazione di qualche incompletezza, spinge alla riflessione e stimola la voglia di conoscere. Per questo motivo si potrebbe presentare l’argomento proprio all’interno di una applicazione concreta, magari legata ad una situazione reale o il più vicina possibile agli studenti.
Inoltre, è preferibile variare metodi e argomenti di studio in modo tale che l’apprendimento sia il meno possibile condizionato da quanto fatto precedentemente. In questo modo l’influenza della storia passata di insuccessi e la conseguente percezione di Sé negativa, di fronte a determinati compiti e attività, verrà notevolmente ridotta.
A mio avviso, tale approccio dovrebbe far comprendere meglio non solo l’importanza delle equazioni, ma di tutta l’algebra e sarebbe auspicabile proseguire su questa strada anche per le disequazioni e i sistemi, partendo per esempio dai problemi di scelta trattati di solito solo nell’ambito della Ricerca Operativa.

TITOLO UNITA’ DIDATTICA                                             “Le Equazioni algebriche”
COLLOCAZIONE CURRICOLARE                        Biennio Scuola Superiore
CLASSE                                                                     Prima (Equazioni di 1° grado)
Seconda (Equazioni di grado superiore al 1°)
TEMPI:                                                                      Classe Prima   6 h per l’attività di classe
2 h per la verifica
Classe Seconda          5 h (Equazioni di 2° grado)
4 h (Equazioni di grado superiore)
2 h per la verifica
OBIETTIVI DIDATTICI GENERALI:

• Imparare a conoscere ed usare le equazioni algebriche ad una incognita, come strumento utile ed efficace per la risoluzione di certi problemi.
• Fornire un esempio in cui può essere utile l’uso di immagini mentali (es. immaginare una bilancia per comprendere meglio il significato di equazione).

OBIETTIVI DIDATTICI SPECIFICI:

• Tradurre in linguaggio algebrico sotto forma di equazione frasi espresse in linguaggio naturale e viceversa.
• Risolvere e discutere equazioni intere e fratte, numeriche e letterali.
• Interpretare graficamente la soluzione di equazioni di 1° e 2° grado.
• Impostare e risolvere problemi di varia natura mediante l’algebra.

PREREQUISITI PER IL 1° ANNO (Equazioni di 1° grado):

• Conoscenza del calcolo numerico e letterale.
• Saper calcolare il valore di espressioni letterali per assegnati valori attribuiti alle lettere.
• Il Piano cartesiano e la Retta per le attività di approfondimento.

PREREQUISITI PER IL 2° ANNO (Equazioni di grado superiore al 1°):

• I prerequisiti del 1° anno.
• Conoscenza del calcolo con i radicali.
• Il Piano cartesiano e la Parabola per le attività di approfondimento.

METODOLOGIA
Questo progetto si pone come obiettivo quello di fornire agli studenti un metodo valido per la risoluzione di certi problemi (quelli risolubili per via algebrica) e allo stesso tempo presentare un argomento classico come quello delle Equazioni algebriche da diversi punti di vista: quello dell’approccio storico, quello che lo vede come un valido strumento per risolvere problemi e come un metodo per imparare a formalizzare le situazioni problematiche. Credo che questo tipo di lavoro sia necessario e utile proprio perché spesso i ragazzi perdono di vista il significato degli oggetti matematici anche se ne fanno un uso appropriato. Mi è capitato, infatti, di vedere che molti non sono in grado di rispondere a domande del tipo: “Cosa è una equazione?”, “Cosa significa risolvere una equazione?”, “Che cosa s’intende per soluzione di una equazione?”.

2 Unità didattica: “Equazioni algebriche di 1° grado ad una incognita”

ARTICOLAZIONE SCHEMATICA DEI CONTENUTI DA TRATTARE IN CLASSE
Gli alunni della classe, che è una Prima, avranno sicuramente sentito parlare di problemi e quasi certamente ne hanno anche risolti molti come per esempio quelli di tipo geometrico o quelli legati a situazioni di vita quotidiana (calcolo del resto, problemi sulla tara, il peso lordo e quello netto, ecc…), quindi è possibile porre le seguenti domande:

• Secondo la vostra esperienza, cosa è un problema?
• Da cosa ci si può accorgere di avere di fronte un problema; da cosa è caratterizzato?

Seguirà una breve discussione durante la quale verranno fornite varie risposte da parte della classe.
Supponiamo che si arrivi ad una idea condivisa da tutti su cosa sia un problema e da cosa è caratterizzato: possiamo affermare che in un problema, noti alcuni elementi (i dati) si chiede di determinarne altri (le incognite), legati ai primi e gli uni agli altri, da un insieme di relazioni; tali relazioni o sono evidenziate esplicitamente dall’enunciato del problema o sono da ricercare.

A questo punto si possono presentare alcuni semplici problemi facilmente risolubili per via intuitiva:

• trovare due numeri naturali pari il cui prodotto è 34;
• trovare due numeri naturali pari il cui prodotto è 28;
• trovare due numeri naturali la cui somma è 8;
• trovare due numeri decimali positivi la cui somma è 8.

Dopo che la classe ha provato a risolvere questi problemi possiamo chiedere agli alunni quale ragionamento hanno messo in atto per la loro risoluzione.
Quindi, come fatto in precedenza, si dovrebbe arrivare alla conclusione che per risolvere un problema occorre mettere a punto una sequenza di azioni che, dalla conoscenza di determinate informazioni iniziali, conduce alla conoscenza di determinate informazioni finali. L’insieme delle informazioni finali è la soluzione del problema.
A questo punto gli alunni dovrebbero aver risolto i problemi proposti, quindi possiamo concludere che:

• il primo problema è impossibile perché nessuna coppia di numeri naturali pari dà 34 come prodotto;
• il secondo problema è determinato perché solo la coppia di numeri 2 e 14 soddisfa la condizione richiesta;
• il terzo problema è anch’esso determinato perché ha come soluzione le coppie di numeri 0 e 8, 1 e 7, 2 e 6, 3 e 5, 4 e 4 e solo loro;
• il quarto problema è indeterminato perché le coppie di numeri decimali positivi che hanno 8 come somma sono infinite; per esempio O e 8, 0,1 e 7,9, 2,3 e 5,7, ...

Riconosciamo quindi facilmente che esistono problemi determinati (che ammettono una o più soluzioni ma in numero finito), indeterminati (ammettono infinite soluzioni), impossibili (non ammettono alcuna soluzione).

Adesso potremmo complicare leggermente la situazione proponendo alla classe, divisa in piccoli gruppi (3 o 4 alunni per gruppo), di tentare di risolvere il seguente problema:
“Uno dei problemi contenuti in una raccolta greca fornisce le seguenti informazioni intorno alla vita di Diofanto (nato nel 250 d.C.): la sua giovinezza durò 1/6 della sua vita, poi la sua barba crebbe per 1/12, si sposò dopo 1/7 e gli nacque un figlio dopo 5 anni. Il figlio visse la metà degli anni del padre e il padre mori 4 anni dopo il figlio.
Il problema consiste nel trovare quanti anni visse Diofanto.”
Nella consegna di questo compito l’insegnante deve chiarire alla classe che non è importante tanto il fatto che loro arrivino a trovare l’età esatta (84 anni) di Diofanto ma piuttosto sapere qual è il ragionamento e quindi la serie di azioni che hanno messo in atto.  
Questo è il metodo algebrico con il quale si può risolvere il problema:

e 84 è la soluzione.
Molto probabilmente solo pochi di loro seguiranno questo modello e visto che non è un problema intuitivo nasce l’esigenza di avere un metodo valido per la sua risoluzione.

Arrivati insieme a questo punto di “crisi” si può iniziare a parlare di Modello di un problema, quindi a come fare per approntare un piano di risoluzione valido. 
Insieme agli alunni si scopre che per questo è necessario seguire i seguenti passaggi:

• Lettura del testo: leggere attentamente l’enunciato del problema per capirne esattamente il significa­to;
• Analisi del testo: individuare chiaramente che cosa è “dato” e che cosa è “richiesto” (distinzione tra dati e incognita, si suppone di trattare, in questa sede, solo i problemi ad una sola incognita);
• Creazione del modello algebrico: l’uso di un opportuno simbolismo, per esempio la scelta della lettera  come simbolo per rappresentare l’entità da ricercare, permette la traduzione del problema in linguaggio algebrico. Dopo questa prima fase si passa a tracciare i passi da seguire per una buona formalizzazione del problema cioè si esprimono in linguaggio algebrico non solo le entità coinvolte ma anche le relazioni tra loro, quindi si imposta quella che si chiama l’equazione risolvente. Si evidenzia così la corrispondenza tra problema ed equazione risolvente, infatti, l’equazione non è altro che un modello del problema;
• Risoluzione all’interno del modello: si passa alla risoluzione tecnica dell’equazione risolvente, per la quale otterremo delle soluzioni. Tenendo conto della corrispondenza tra problema ed equazione, notiamo come appunto trovando le soluzioni dell’equazione risolvente si possano ottenere le soluzioni del problema dato;
• Valutazione dell’attendibilità dei risultati: occorre sempre fare una verifica delle soluzioni trovate, analizzando se queste soddisfano le con­dizioni richieste. Una soluzione, per essere accettabile, deve soddisfare non solo le relazioni matematiche formulate all’interno del modello ma anche i requisiti caratteristici degli enti in questione.

In questa breve scaletta, nella quale sono elencati i punti da seguire per la creazione del modello algebrico di un problema, si è parlato di dati, di incognita, di simboli (la x in particolare), di equazione risolvente e di risoluzione della stessa. Con il problema sull’età di Diofanto si è presentata la necessità di trovare un metodo o meglio un modello che traducesse abbastanza fedelmente il problema dato e che permettesse con poca fatica di trovarne la soluzione; la scaletta che è stata presentata non vuole essere la ricetta per la creazione di un tale modello e per questo motivo non verrà presentata alla classe così come è stata scritta ma proprio durante il lavoro in classe gli alunni, insieme all’insegnante, davanti ad un certo problema, esploreranno i passi della scaletta scoprendoli man mano che servono. 

Vediamo quindi come, da un problema, è possibile definire tutto l’apparato di argomentazioni che gira intorno alle equazioni algebriche: si propone agli alunni un problema come il seguente
“Un mattone pesa 1 kg più mezzo mattone. Quanto pesa un mattone?”
e si chiede loro come si comporterebbero per trovare la soluzione cercando allo stesso tempo di farli lavorare sulla creazione di un modello secondo i passi visti in precedenza.
Se non dovesse arrivare alcun suggerimento si può procedere così: insieme alla classe si nota che dopo la lettura e l’analisi del testo emerge il fatto che il problema chiede di stabilire il peso di un mattone. Per pesare gli oggetti di solito si usano le bilance, quindi si può pensare di prendere una bilancia a piatti, per esempio, e procedere secondo il seguente ragionamento:

Si fa notare alla classe il fatto che il procedimento usato funziona perché ha permesso di trovare il peso di un mattone ma risulta molto scomodo risolvere problemi come quello proposto facendo uso di veri mattoni e bilance. I disegni che li rappresentano costituiscono già un metodo risolutivo più semplice, ma ancora piuttosto laborioso. Potremmo dire che questi modelli non sono proprio ideali. L’obiettivo a questo punto è vedere come, con il calcolo letterale e le equazioni, è possibile costruirne uno più comodo e funzionale: tali strumenti, infatti, ci permettono di svolgere gli stessi ragionamenti ma in modo simbolico e di arrivare alla soluzione più rapidamente.
Allora con la classe, una volta individuati i dati e l’incognita, possiamo concordare di usare la lettera x per indicare il peso di un mattone (espresso in kg), quindi la situazione rappresentata in Fig.1 può essere espressa in forma simbolica nel seguente modo:

L’equazione risolvente dunque traduce il problema in simboli algebrici ossia crea il modello algebrico della situazione proposta. Abbiamo parlato di equazione risolvente, ma cosa è una equazione?

Insieme alla classe quindi, si rivedono i passaggi che ci hanno condotto alla soluzione seguendo la via sperimentale e si nota che, a questo punto, possono essere così schematizzati:

L’equazione finale, oltre a rappresentare simbolicamente la situazione descritta nella Fig. 3, fornisce la soluzione del problema proposto: infatti, ci dice che il peso di un mattone è uguale a 2Kg.

Adesso, sempre in collaborazione con la classe, possiamo arrivare ad affermare che un’equazione (ad un’incognita) è un’uguaglianza tra due espressioni letterali verificata solo per certi particolari valori attribuiti alla lettera, scelta come incognita.

In generale, per risolvere un’equazione si segue un procedimento simile a quello ora visto: si trasforma l’equazione data in una più semplice e questa a sua volta in un’altra ancora più semplice, fino ad ottenere un’equazione che, come la  ci permetta di determinare in modo immediato l’insieme delle soluzioni. Affinché questo procedimento ci conduca effettivamente alla risoluzione dell’equazione da cui siamo partiti occorre che le equazioni via via ottenute abbiano le stesse soluzioni dell’equazione iniziale, siano in altre parole equivalenti all’equazione iniziale.

Prima di arrivare con gli alunni al concetto d’equazione equivalente ad una data, occorre fare un’osservazione, che però non interessa direttamente la classe: nei libri di testo si leggono frasi del tipo “due equazioni (algebriche nella stessa incognita x) si dicono equivalenti se hanno le stesse soluzioni”; si tratta di una definizione in realtà ambigua perché sarebbe necessario specificare l’ambito numerico nel quale s’intende operare, per esempio  e  sono equazioni equivalenti in N,, perché hanno come soluzione il numero 2, ma non lo sono in Z, Q, R, C perché la prima equazione ha l’unica soluzione 2, la seconda ha due soluzioni 2 e –2. Questo succede perché normalmente si dà per scontato che si lavora in R, mentre sarebbe opportuno dire: “Fissato l’insieme numerico nel quale si vuole operare, due equazioni algebriche nella stessa incognita x, si dicono equivalenti se hanno lo stesso insieme di soluzioni rispetto all’insieme numerico considerato”.
Come arrivare ad una tale definizione con la classe?
Si potrebbe chiedere agli alunni come definirebbero equazioni del tipo:  e poi porre le seguenti domande: “Sono diverse ma, hanno qualcosa in comune? Come vengono chiamate figure piane diverse che però hanno la stessa area?”.
Dopo questa breve discussione possiamo chiedere agli alunni di trovare le proprietà della relazione d’equivalenza tra equazioni e quindi far emergere che:

• ogni equazione è equivalente a se stessa (Proprietà riflessiva);
• se un’equazione è equivalente ad una seconda equazione, allora questa è equivalente alla prima (Proprietà simmetrica);
• se due equazioni sono equivalenti ad una terza, allora sono equivalenti tra loro (Proprietà transitiva).

Seguendo i procedimenti esposti in precedenza e richiamati nel seguente schema:

si scopre con la classe in quali casi e in che modo è possibile trasformare un’equazione in un’altra ad essa equivalente. Questi modi non sono delle regole ma sono avvalorati e generalizzati da due principi, detti Principi d’equivalenza che andremo a scoprire.
Riprendendo in considerazione l’equazione risolvente , vediamo di capire cosa sta dietro la formulazione dei “Principi d’equivalenza”:

La validità dei “Principi d’equivalenza” è assicurata dal fatto che nell’ambito numerico nel quale si opera, cioè il campo dei reali, le trasformazioni codificate nei “Principi d’equivalenza” sono invertibili (grazie alle proprietà delle operazioni aritmetiche definite in R).
In generale, per risolvere un’equazione si cerca di trasformarla, applicando tali Principi, in un’altra ad essa equivalente, ma di forma più semplice; questa, a sua volta, si trasforma in un’altra equivalente di forma ancora più semplice e così di seguito, finché si perviene ad un’equazione equivalente alla data, della quale si sappiano con immediatezza trovare le soluzioni.

Allora cosa s’intende per soluzione di un’equazione? Facendo riferimento al problema del mattone possiamo concludere con gli alunni che, la soluzione o radice di un’equazione non è altro che ogni valore numerico che attribuito all’incognita soddisfa l’uguaglianza, cioè fa assumere lo stesso valore ad entrambe le scritture poste a destra e a sinistra dell’uguale. Quindi risolvere un’equazione significa trovare le sue soluzioni.

Abbiamo visto che l’equazione risolvente non è altro che il modello algebrico del nostro problema e che la soluzione dell’equazione è soluzione del problema stesso (va comunque osservato che questo non è sempre vero, può succedere che alcune soluzioni trovate nel modello non possano essere accettate nel problema e quindi è opportuno verificare la validità delle soluzioni trovate; è possibile presentare quest’eventualità alla classe fornendo degli esempi opportuni), quindi come esistono problemi determinati, impossibili e indeterminati così possiamo dire per le equazioni:

• se un’equazione ammette una sola soluzione diciamo che è determinata;
• se un’equazione è priva di soluzioni si dice che è impossibile;
• se un’equazione ammette infinite soluzioni si dice che è indeterminata oppure che è un’identità.

In precedenza abbiamo detto che “un’equazione ad un’incognita è un’uguaglianza tra due espressioni letterali verificata solo per certi particolari valori attribuiti alla lettera scelta come incognita.”
Nella risoluzione del nostro problema, si può notare che, data l’equazione nell’incognita x ,

è possibile, mediante l’applicazione dei Principi d’equivalenza, scrivere l’equazione nella forma
.
Ci si può facilmente rendere conto che questo è possibile in generale: data un’equazione in cui compaiono solo espressioni algebriche razionali in una sola incognita x , è sempre possibile scrivere l’equazione nella forma canonica

dove  è un polinomio nella lettera x. Il grado del polinomio è il grado dell’equazione.
Le equazioni come la risolvente del problema del mattone si dicono equazioni algebriche di 1° grado ad un’incognita perché possono essere scritte nella forma canonica
 
dove  e  sono numeri reali. Come si può vedere, la scrittura a sinistra dell’uguale è proprio un polinomio di 1° grado nella lettera x.
Nel nostro caso, cioè per la , abbiamo che  e .

ATTIVITA’ DI APPROFONDIMENTO:
Dopo un tale lavoro, l’attività di classe potrebbe essere organizzata scegliendo alcuni di questi approfondimenti:

• assegnare esercizi utili come verifica e come visione di casi più articolati (es. equazioni numeriche e letterali intere e fratte; facendo particolare attenzione a far notare, nel caso delle equazioni letterali, la differenza tra parametro e incognita);
• proporre problemi da tradurre in un modello e quindi risolvere trovando le soluzioni dell’equazione risolvente;
• assegnare dei lavori di gruppo per l’approfondimento dell’argomento da un punto di vista storico in particolare sullo sviluppo del simbolismo algebrico;
• organizzare un lavoro nel Laboratorio Informatico dove, con l’utilizzo del software Derive è possibile acquisire meglio il significato di equazioni impossibili e indeterminate e anche verificare l’interpretazione grafica della soluzione di un’equazione.

Ricerche di gruppo sull’evoluzione dei problemi nella storia delle attività dell’uomo con particolare riferimento allo sviluppo del simbolismo algebrico
Il problema sull’età di Diofanto è tratto da una raccolta greca, questo significa che già a quell’epoca si cercava di risolvere problemi di varia natura. Quest’osservazione permette l’apertura di una piccola parentesi storica che, a mio parere, aiuta a vedere la matematica non più solo come disciplina tecnica ma come una scienza che ha una sua storia ed una continua evoluzione.
L’insegnante potrebbe delineare i vari approcci ai problemi usati dalle antiche civiltà fino al Rinascimento quindi far notare come queste attività abbiano portato, nell’arco di molti secoli, a quello che è adesso l’algebra (limitandosi a quella scolastica):

presso tutte le più antiche civiltà sia la geometria che l’a­ritmetica nacquero proprio per risolvere problemi di vita quotidiana: misurare terreni, calcolare quantità di merci, descrivere e registrare ac­cordi di contratti di compravendita e così via. A noi sono giunti diversi testi (conservati su tavolette di argilla, papiri o altri analoghi supporti) di antichi popoli vissuti centinaia e centinaia di anni prima di Cristo, che mostrano come questi popoli usassero la ma­tematica per risolvere problemi, a volte anche piuttosto complessi.
Le equazioni di 1° grado venivano risolte “per tentativi” fin dai tempi più remoti; solo con l’introduzione della “Regola d’Algebra” da parte dei matematici arabi, si può parlare di risoluzione in senso moderno. Vediamo i passaggi storici seguendo lo schema:

Babilonesi Intorno al 2000 a.c.	I Babilonesi seguivano una linea di pensie­ro molto analoga alla nostra, anche se non possedeva­no la nostra moderna simbologia. Descrivevano quindi i loro proce­dimenti mediante esempi numerici. Nei loro testi trovia­mo infatti diversi problemi risolti nello stesso modo e alla fine troviamo la frase di conclusione: "tale è il procedimento”.
Egizi Intorno al 1600 a.C.	Nei papiri si trovano soluzioni di problemi contenenti un’incognita che sono nel complesso paragonabili alle nostre equazioni di 1° grado in un’incognita. I problemi venivano enunciati verbalmente insieme con delle semplici regole per ottenere le soluzioni, ma senza spiegare perché venissero usati quei metodi e perché funzionassero.
Greci Nel III secolo d.C.	Oltre che di geometria, i Greci si sono occupati anche di problemi che venivano risolti con tecniche algebriche. Non veniva usato alcun simbolismo né venivano date giustificazioni sull’uso dei metodi applicati. I problemi che conducevano a delle equazioni per essere risolti, diventarono una forma comune di indovinelli ed enigmi. Diofanto chiamava l’incognita “il numero del problema”.
Arabi Nel IX secolo d.C.	Agli Arabi dobbiamo la nostra notazione posizionale dei numeri così come i loro simboli ma, questo non è stato il solo contributo alla matematica. Nell’opera “Al-gebr we’l mukabala” scritta nell’830 d.C. da Mohammed al-Khowarizmi (opera che dà il nome all’Algebra) troviamo una trattazione ampia e dettagliata sui metodi risolutivi delle equazioni algebriche corredati da esempi. L’incognita viene chiamata “cosa” o “radice di una pianta” e da questo deriva il nostro termine “radice” per indicare la soluzione di un’equazione.
Medioevo Intorno al 1200	In Europa si sviluppa il commercio estero con gli Arabi e questo portò a numerosi contatti anche tra gli studiosi dei vari paesi. Leonardo Pisano (1170-1250) detto Fibonacci, con il suo “Liber Abaci”, introduce in Europa il sistema di numerazione arabo e i metodi risolutivi delle equazioni algebriche trattate dagli arabi. L’obiettivo del Fibonacci era quello di fornire metodi pratici per la gestione dei conti dei commercianti dell’epoca ed il termine “equazione” compare per la prima volta nella sua opera.
Rinascimento Intorno al 1500	Gran parte dell’interesse cinquecentesco per l’algebra era motivato dalla necessità di risolvere i problemi, quindi le equazioni. Anche le attività commerciali e bancarie che si stavano allora sviluppando richiedevano un’aritmetica più avanzata. Per “Regola d’Algebra” i matematici del Rinascimento intendevano quel procedimento per la risoluzione dei problemi aritmetici che consiste nella messa in equazione, nella riduzione dell’equazione in forma canonica e nell’effettiva risoluzione dell’equazione ottenuta.

Le operazioni previste nella “Regola d’Algebra” usata nel Rinascimento, presuppongono quello che viene chiamato calcolo algebrico; è evidente (come abbiamo sperimentato con il problema del mattone) che l’esecuzione di tale calcolo è favorita dall’uso di un simbolismo opportuno, quindi il progresso nel campo dell’algebra fu l’introduzione di un simbolismo migliore.
Prima del 1500 l’unico studioso che avesse coscientemente introdotto un simbolismo per rendere il ragionamento algebrico più compatto e più efficace era stato proprio Diofanto che si presume usasse il simbolo  per indicare l’incognita. Tutti gli altri cambiamenti di notazione erano essenzialmente delle abbreviazioni di parole comuni introdotte piuttosto casualmente. Nel Rinascimento lo stile consisteva nell’uso di parole, di abbreviazioni e, naturalmente dei simboli numerici. Oggi molti problemi vengono affrontati mediante sofisticate metodologie e tecniche di calcolo, mediante creazione di modelli matematici che traducono in equazioni e relazioni le principali caratteristiche di una questione, ma il cammino che ha portato l’algebra a diventare quella che è oggi è stato molto lungo e faticoso.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Il lungo cammino dei simboli matematici

L’algebra nei primi tempi del suo sviluppo (prima del 1600) mancava di abbreviazioni e di simboli adeguati e veniva ancora espressa a parole. Era pertanto laborioso scrivere operazioni e relazioni matematiche e interpretare scritture senza conoscere i simboli utilizzati dai matematici (ogni matematico ne introduceva di propri a piacimento). Era quindi necessario trovare simboli che per la loro semplicità e immediatezza diventassero il più possibile co­muni. Il cammino per convergere su un simbolismo ac­cettato dalla comunità dei matematici fu lungo e acci­dentato e può essere così riassunto:

Per indicare le incognite Diofanto nel III secolo d.C. già utilizzava delle lettere

Fibonacci nel XIII secolo usava i segni p e m per indicare le abbreviazioni delle parole latine plus e minus

I mer­canti tedeschi utilizzavano + o - per denotare i pesi in ec­cesso o in difetto delle cassette

Solo più tardi, nel 1481, + e - assunsero il significato di addizione e sottrazione

Nel XV secolo indicavano l'incognita ancora con la parola res (in latino), cosa (in italiano), coss (in tedesco)

Il segno  della moltiplicazione introdotto da Oughtred (1574-1660) fu ostacolato perché poteva es­sere confuso con la lettera dell'alfabeto “x”

La sbarretta orizzontale della frazione già nota agli Arabi venne usata da Fibonacci ma comunemente adottata solo nel XVI secolo

La sbarretta obliqua per la divisione venne introdotta addirittura nel 1845

Il segno “=” fu introdotto nel 1557 da Robert Recorde

Il segno di radice, prima indicato con la lettera R fu adottato nel secolo XVI

L'uso degli esponenti si trova nell'algebra di Bombelli del XVI secolo

Le parentesi tonde appaiono nel 1544, le quadrate e graffe risalgono al 1593

Fu Viète nel 1591 a introdurre le lettere sia per le incognite che per le quantità note

Con dei miglioramenti apportati al simbolismo di Viete, soprattutto da parte di Cartesio (x,y,z per le incognite; a,b,c,… per le quantità note) siamo arrivati ad avere alla fine del XVI secolo uno strumento la cui potenza sarà apprezzata sino ad oggi.

Dall’inizio del XVIII secolo, l’algebra diventa la “Scienza del calcolo letterale” (l’algebra scolastica), cioè la scienza delle trasformazioni di formule formate da lettere.

Interpretazione grafica delle soluzioni di una equazione di 1° grado ad una incognita
Presupponendo il Piano Cartesiano e l’equazione di una retta come concetti e strumenti acquisiti dalla classe si può riprendere (anche dopo del tempo) l’argomento delle equazioni algebriche di 1° grado partendo per esempio dall’equazione risolvente del problema del mattone

e considerare la sua equivalente
.
Se prendiamo la scrittura

possiamo chiedere alla classe cosa rappresenta nel piano cartesiano. Si tratta dell’equazione di una retta, quindi cosa significa da questo punto di vista risolvere l’equazione ?
Insieme alla classe, dopo aver disegnato la retta sul piano cartesiano e visto che passa per il punto , si arriva alla conclusione che risolvere l’equazione equivale a cercare l’ascissa del punto di intersezione tra la retta e l’asse delle x.

Per una ulteriore verifica è possibile usare Derive e ottenere la seguente situazione:

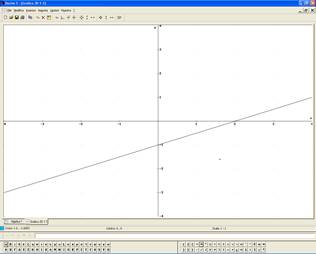
Altre considerazioni sono ovviamente opportune considerando equazioni impossibili (rette parallele all’asse x) e equazioni indeterminate (l’asse x stesso).

Equazioni al computer
Potendo utilizzare il Laboratorio Informatico potrebbe essere interessante far elaborare ai ragazzi dei programmi per la risoluzione di equazioni usando linguaggi di programmazione come il Pascal o il Visual Basic oppure si può far ricorso a diverse applicazioni con Derive. Possiamo utilizzare Derive per osservare e meglio comprendere i procedimenti algebrici oppure per risolvere direttamente e velocemente equazioni con il comando Risolvi:
Obiettivo: ripassare la procedura di soluzione di equazioni algebriche attraverso l’aiuto di Derive per risolvere equazioni algebriche:
Consegna iniziale: risolvere l’equazione  applicando la normale procedura di risoluzione algebrica e poi risolvere la stessa equazione con il comando Risolvi di Derive.

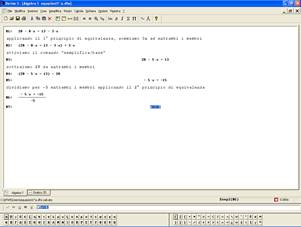
Abbiamo usato Derive per compiere le stesse procedure che mettiamo in atto manualmente nella risoluzione di un’equazione.

Vediamo adesso come usare Derive per calcolare direttamente il risultato:

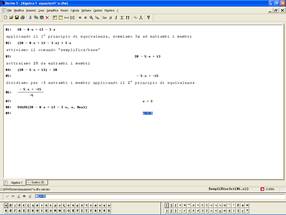
E’ anche possibile sperimentare e fare osservazioni utili sui casi interessanti delle equazioni impossibili e indeterminate (Derive fornisce come risultato False e True rispettivamente), chiedendo ai ragazzi perché secondo loro si ottengono quei risultati come soluzione.
Si può procedere così:
data l’equazione  risolviamola in automatico con Derive:

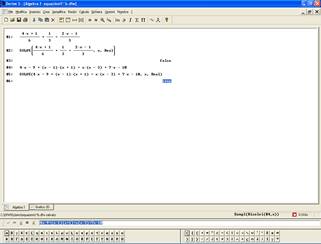
il risultato fornito da Derive è False. Perché?
Facciamo la stessa cosa per l’equazione , cosa darà Derive? Perché?

Derive, quindi, può servire non solo a farci risparmiare la fatica del calcolo ma anche a dare un senso a certi risultati. Non solo: il fatto che l’equazione deve essere scritta a mano nella riga di inserimento in basso, fa sì che lo studente comprenda meglio l’importanza delle parentesi e cosa significa avere un numero davanti ad una lettera ().

3 Unità didattica: “Equazioni algebriche di grado superiore al 1°”

 

3.1 Equazioni algebriche di 2° grado

ARTICOLAZIONE SCHEMATICA DEI CONTENUTI DA TRATTARE IN CLASSE
Nel caso in cui la classe è la stessa che dalla Prima è passata in Seconda, è possibile riprendere il discorso sulla creazione del modello algebrico di un problema e quindi chiedere agli alunni di ricostruire i passaggi utili alla individuazione e creazione di un valido modello che risolva un dato problema. Se invece si lavora in tale classe per la prima volta, prima di tutto è necessario affrontare il problema della modellizzazione, quindi partendo da un dato problema ricostruire con gli alunni i passaggi utili alla costruzione del modello algebrico.
Una volta che, con la classe, si sono richiamati in causa i passi da compiere per la creazione del modello, come per le equazioni di 1° grado è possibile arrivare alla soluzione di una di 2° grado e costruirne anche la Formula Risolutiva.
Si comincia con il proporre agli alunni un problema come il seguente:
“Utilizzando 240m di filo spinato si vuole recintare un appezzamento di terreno, di forma rettangolare, della superficie di 3200m². Quali dimensioni dovrà avere tale appezzamento?”
e si chiede loro di costruirne un modello algebrico.
Quindi insieme alla classe si cerca, usando un opportuno simbolismo, di impostare l’equazione risolvente: il problema chiede di stabilire le due dimensioni dell’appezzamento che ha forma rettangolare. Il fatto che si vuole recintare tale appezzamento con 240mdi filo spinato significa che tale quantità rappresenta la misura del perimetro del rettangolo. Allora 120m è la misura del semiperimetro. Indicando con x una delle due dimensioni, l’altra sarà :

La superficie dell’appezzamento misura 3200m², quindi possiamo scrivere in termini simbolici
.
La classe non avrà difficoltà a riconoscere in tale scrittura un’equazione e, visto che traduce il problema in simboli algebrici, essa non è altro che l’equazione risolvente.

Adesso si pone il problema di come risolvere una tale equazione perché ci si accorge che non è di 1° grado, quindi dopo averla identificata, sempre usando i Principi d’Equivalenza, andremo a risolverla e quindi a costruire la Formula Risolutiva.

Gli alunni sanno dall’anno passato che per risolvere un’equazione di 1° grado si cerca di trasformarla, applicando i Principi d’Equivalenza, in un’altra a essa equivalente, ma di forma più semplice e così di seguito, finché si perviene ad un’equazione equivalente alla data, della quale si sappiano con immediatezza trovare le soluzioni.
Ci si accorge però che per la nostra equazione

non è così semplice trovarne una equivalente, della quale sia immediato trovare la soluzione, perché se andiamo a svolgere la moltiplicazione a sinistra dell’uguaglianza otteniamo la seguente scrittura

che, opportunamente modificata, diventa
.
I ragazzi riconosceranno che si tratta di un polinomio di 2° grado nella lettera x posto uguale a 0.
Questo non ci dovrebbe stupire molto perché, già l’anno passato avevamo visto che, data una equazione in cui compaiono solo espressioni algebriche razionali in una sola incognita x, è sempre possibile, mediante l’applicazione dei Principi d’Equivalenza, scrivere l’equazione nella forma canonica

dove  è un polinomio nella lettera x e il grado del polinomio è il grado dell’equazione.
Le equazioni come la risolvente del problema posto si dicono equazioni algebriche di 2° grado ad una incognita perché possono essere scritte nella forma canonica

dove  , e  sono numeri reali.
Nel nostro caso, cioè per l’equazione , abbiamo che , , .

Con la classe siamo riusciti ad identificare l’equazione risolvente del dato problema come equazione di 2° grado nell’incognita x, ma non siamo ancora riusciti a trovarne la soluzione. Per fare questo prendiamo in considerazione l’equazione di 2° grado generica scritta nella forma canonica e vediamo, insieme alla classe, di trovare un modo per individuarne la soluzione. Il lavoro da fare insieme agli alunni è schematizzato nella seguente tabella:

La scrittura che abbiamo ottenuto alla fine si chiama Formula Risolutiva per le equazioni algebriche di 2° grado in una incognita, perché è l’espressione che con immediatezza (facendo semplici calcoli) ci fornisce la soluzione dell’equazione data.
Vista l’espressione a destra dell’uguaglianza

si può chiedere agli alunni se notano qualcosa di particolare degno di attenzione. Notiamo che è presente una scrittura sotto il segno di radice quadrata e, sappiamo dalle proprietà dei radicali in R che,  esiste solo se .
Si è soliti indicare l’espressione  con la lettera greca maiuscola  (delta) e si chiama discriminante dell’equazione
.
La scelta di usare la parola discriminante è dovuta ad un motivo che si può scoprire: possiamo lasciare agli alunni il compito di individuare il tipo di soluzioni per ciascuno dei casi ,  e , quindi far sì che arrivino da soli a capire il motivo di tale scelta (il discriminante rende differenziate, cioè discrimina, le soluzioni dell’equazione) e arrivare così insieme a loro al seguente schema riepilogativo dove con S indichiamo l’insieme delle soluzioni:

            Si lascia quindi alla classe il compito di trovare l’insieme soluzione dell’equazione risolvente del problema da cui siamo partiti. C’è la possibilità di usare la formula ridotta visto che  quindi, dopo che hanno provato ad usare la formula completa


ed hanno riconosciuto la laboriosità dei calcoli che ne conseguono, si potrebbe chiedere loro di riflettere sulla struttura della scrittura a destra dell’uguaglianza e tentare insieme di costruire la Formula ridotta ponendo , allora otteniamo

 che equivale a .
Con la Formula ridotta i calcoli sono molto più agevoli e quindi non è difficile trovare la soluzione:

Si potrebbe chiedere alla classe: “Se avessimo ottenuto una soluzione negativa, cosa avremmo dovuto concludere?” (l’incognita rappresentava nel problema una dimensione dell’appezzamento).

ATTIVITA’ DI APPROFONDIMENTO:
Come per le equazioni di 1° grado, anche in questo caso l’attività di classe potrebbe essere organizzata scegliendo alcuni tra questi approfondimenti:

• assegnare esercizi utili come verifica e come visione di casi particolari (es. equazioni incomplete, equazioni numeriche e letterali fratte, equazioni risolubili mediante la Legge dell’annullamento del prodotto);
• proporre problemi da tradurre in un modello e quindi risolvere trovando le soluzioni dell’equazione risolvente;
• assegnare dei lavori di gruppo nei quali ricercare le origini storiche della Formula Risolutiva;
• proporre una attività di ricerca e scoperta delle relazioni esistenti tra i coefficienti e le soluzioni di una equazione di secondo grado;
• con Derive è possibile fare un lavoro simile a quello svolto nel caso delle equazioni di primo grado.

Ricerca delle origini storiche della Formula Risolutiva
L’insegnante potrebbe delineare quali sono stati nella storia i vari tentativi di risoluzione di equazioni di 2° grado, con quali esiti ed in quali contesti applicativi sono avvenuti. Quindi far notare come il problema della risoluzione “per radicali” (metodo con cui è possibile ottenere le soluzioni di una equazione mediante un numero finito di operazioni razionali e di estrazioni di radice, eseguite sui coefficienti dell’equazione) delle equazioni algebriche abbia interessato matematici di tutti i tempi:
per quanto riguarda le equazioni di 2° grado, il più antico metodo di risoluzione di cui si abbia notizia è quello che abbiamo usato noi. Tale metodo era presumibilmente già noto ai due matematici greci Erone e Diofanto (III° secolo d.C.), ma anche presso le civiltà più antiche troviamo problemi concreti risolti mediante l’uso di equazioni di 2° grado

Ricerca e scoperta delle relazioni tra le soluzioni e i coefficienti di un’equazione di 2° grado
Data l’equazione , abbiamo visto che se  le soluzioni sono
 e .
A questo punto possiamo chiedere agli alunni, cosa succede, secondo loro, se faccio la somma ed il prodotto di queste soluzioni. Si lascia quindi a loro il compito di scoprire le relazioni tra i coefficienti e le soluzioni dell’equazione:
.

Interpretazione grafica delle soluzioni di un’equazione di 2° grado ad un’incognita
Presupponendo il Piano Cartesiano e l’equazione di una parabola come concetti e strumenti acquisiti dalla classe si può cercare di dare una interpretazione grafica alle soluzioni di una equazione di 2° grado. Prendiamo l’equazione seguente

se consideriamo la scrittura

possiamo chiedere agli alunni cosa rappresenta nel piano cartesiano. Si tratta dell’equazione di una parabola, quindi cosa significa da questo punto di vista risolvere l’equazione ? Gli alunni potrebbero rispondere (avendo già lavorato con i sistemi) che tale equazione non è altro che la risolvente del sistema

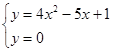
quindi non dovrebbero avere problemi ad affermare che risolvere l’equazione  equivale a cercare le ascisse dei punti di intersezione tra la parabola e l’asse delle x. Se queste risposte non dovessero arrivare dalla classe si può procedere semplicemente disegnando la parabola sul piano cartesiano e verificare che tale parabola passa proprio per i punti  e .
Per una ulteriore verifica è possibile usare Derive e ottenere la seguente situazione:

A questo punto è utile fare delle considerazioni circa le equazioni impossibili (parabole non secanti l’asse x) e quelle con due soluzioni coincidenti (parabole tangenti l’asse x), ponendo agli alunni domande per spingerli a scoprire da soli cosa si ottiene in tali casi dal punto di vista grafico e perché.

Equazioni al computer.
Come per le equazioni di 1° grado, è possibile far elaborare ai ragazzi dei programmi per la risoluzione di equazioni di 2° grado usando linguaggi di programmazione come il Pascal o il Visual Basic; in più, in questo caso, con la struttura condizionale IF-THEN-ELSE è più facile capire il significato del discriminante. Al solito, con Derive possiamo risolvere direttamente e velocemente equazioni con il comando Risolvi:
Consegna: risolvere l’equazione  applicando la normale procedura di risoluzione algebrica e poi risolvere la stessa equazione con il comando Risolvi di Derive

 

3.2 Equazioni algebriche di grado superiore al 2°

ARTICOLAZIONE SCHEMATICA DEI CONTENUTI DA TRATTARE IN CLASSE:
Avendo identificato le equazioni di 1° e 2° grado in un’incognita come quelle scritte nella forma  dove  è un polinomio, rispettivamente, di primo e secondo grado, potremmo porre alla classe le seguenti domande:
“Se esistono le equazioni di grado superiore al secondo, in che modo possono essere scritte?”
“Saranno associate a polinomi di grado superiore al 2°?
e poi
“Ci sono situazioni problematiche la cui “modelizzazione” porta ad una equazione di 3° o 4° grado?”
oppure
“Riuscite a trovare un problema la cui risoluzione porti ad esempio ad un’equazione di 3° grado?”

Se la classe riesce a trovare un tale problema su può lavorare su quello, altrimenti si può prendere in considerazione il seguente:
“Si deve costruire una vasca di calcestruzzo, aperta in alto, che esternamente sia a forma di cubo; le pareti e il fondo devono avere spessore di 20 cm e la capacità deve essere di 288 litri. Determinare le misure della vasca.”
e si chiede loro di costruirne un modello algebrico.
Quindi insieme alla classe, si cerca di tradurre il problema in un modello per poi arrivare ad impostare l’equazione risolvente, che in questo caso sarà di 3° grado. Il problema chiede di stabilire le misure della vasca che ha forma cubica; la prima cosa da fare è portare le misure alla stessa unità di misura: visto che la capacità, cioè il volume, è espressa in litri (dm³) portiamo lo spessore da 20 cm a 2 dm.
Indicando con x la misura del lato (esterno) del cubo e tenendo conto dello spessore delle pareti e del fondo,

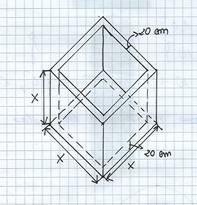
il volume interno della vasca è dato dalla relazione .
La capacità deve essere di 288 litri, cioè di 288 dm³, allora avremo che
.
Se andiamo a svolgere la moltiplicazione a sinistra dell’uguaglianza e operiamo le dovute semplificazioni otteniamo la seguente scrittura

Si tratta di un polinomio di 3° grado nella lettera x posto uguale a 0.

Per quanto già osservato nel caso delle equazioni di 1° e 2° grado, un’equazione algebrica nell’incognita x  è sempre possibile scriverla nella forma canonica

dove  è un polinomio nella lettera x. Il grado del polinomio è il grado dell’equazione.
Le equazioni come la risolvente del problema posto si dicono equazioni algebriche di 3° grado ad u’ incognita.

Come è facile immaginare, possiamo incontrare equazioni algebriche anche di grado superiore al 3°, basta pensare alla scrittura  dove  è un polinomio di 4° o 5° grado e così via.
Mentre per le equazioni di 1° grado la risoluzione è piuttosto semplice e per quelle di 2° grado basta ricorrere alla Formula risolutiva, per le equazioni di grado superiore al 2° non c’è un metodo universalmente valido (della risoluzione per radicali parleremo meglio negli approfondimenti).
A partire da degli esempi, vedremo come la risoluzione di molte equazioni di grado superiore al 2° possa essere ricondotta, mediante opportune tecniche, alla risoluzione di più semplici equazioni di 1° e 2° grado. Quindi si presentano alla classe i due metodi utili a tale scopo: il cambiamento di variabile e la scomposizione in fattori.

Tornando alla nostra equazione
 
utilizziamo il metodo della scomposizione in fattori: con la classe notiamo subito che la scrittura di sinistra è un polinomio di 3° grado che non è lo sviluppo del cubo di un binomio, quindi proviamo a fattorizzare usando la Regola di Ruffini. Otteniamo così l’equazione

equivalente alla data.
Osservando la scrittura concordiamo con la classe di applicare la Legge dell’annullamento del prodotto per la ricerca delle soluzioni: il prodotto a sinistra può essere uguale a zero se e solo se almeno uno dei due fattori è uguale a zero

Così la risoluzione dell’equazione di 3° grado è stata ricondotta alla risoluzione di due equazioni più semplici, rispettivamente di 1° e 2° grado. Lasciando agli alunni il compito di risolvere le due equazioni così ottenute, facendo particolare attenzione a quella di 2° grado per la quale non è necessario ricorrere alla Formula risolutiva perché basta osservare che  non sarà mai uguale a zero, si ha che l’equazione di 3° grado ha per soluzione , che in termini del problema significa che il lato esterno del cubo deve misurare 10 dm.

Riguardo alla formalizzazione del problema posto, è ovviamente possibile anche scegliere di indicare con x la misura del lato interno della vasca: in tal caso il volume della vasca è dato dalla relazione , quindi l’equazione che ne discende è , la cui soluzione è ; il lato esterno della vasca deve quindi misurare dm ( i 4 dm dovuti allo spessore).

ATTIVITA’ DI APPROFONDIMENTO:
Come per le equazioni di primo grado, anche in questo caso l’attività di classe potrebbe essere organizzata scegliendo alcuni tra questi approfondimenti:

• assegnare esercizi utili come verifica e come visione di casi particolari (es. equazioni binomie, equazioni biquadratiche, equazioni fratte);
• proporre problemi da tradurre in un modello e quindi risolvere trovando le soluzioni dell’equazione risolvente;
• assegnare dei lavori di ricerca storica nei quali indagare sulla esistenza della Formula risolutiva delle equazioni di grado superiore al 2°;
• con Derive è possibile fare un lavoro simile a quello svolto nel caso delle equazioni di 1° e 2° grado, lasciando ancora di più ai ragazzi il compito di provare e scoprire.

Ricerca sulla esistenza della Formula Risolutiva per le equazioni di 3° grado e grado superiore
L’insegnante potrebbe delineare gli eventi storici che hanno portato alla scoperta della Formula risolutiva per le equazioni di 3° e 4° grado e, allo stesso tempo far emergere le ricerche che hanno portato alla dimostrazione che un’equazione algebrica di grado maggiore o uguale al 5° non è risolubile “per radicali” (cioè non è possibile ottenere le soluzioni mediante un numero finito di operazioni razionali e di estrazioni di radice, eseguite sui coefficienti dell’equazione), in altre parole non esiste la formula risolutiva, simile a quella vista per le equazioni di 2°. Questo non significa che non sia possibile in alcun modo risolvere equazioni di grado superiore al 4° infatti, l’insuccesso del tentativo di trovare una formula risolutiva per radicali per equazioni di grado superiore al 4° stimolò la ricerca di metodi di risoluzione per approssimazione, validi per equazioni di grado qualunque. I metodi di risoluzione per approssimazione sono anche chiamati Metodi numerici e sono gli stessi usati dai calcolatori elettronici.
Il problema della risoluzione “per radicali” delle equazioni algebriche ha interessato matematici di tutti i tempi: già nel 2000 a.C., gli antichi Babilonesi erano in grado di risolvere oltre alle equazioni di 1°grado, anche quelle di 2° e la formula risolutiva che noi conosciamo era nota fin dai tempi dei greci. Nell’opera “Arithmetica” di Diofanto, troviamo infatti una raccolta di problemi risolti attraverso equazioni e sistemi di equazioni di 1° e 2°grado. Per le equazioni di 3° grado la formula risolutiva fu trovata solo all’inizio del 1500, anche se equazioni di 3° grado particolari si trovano risolte anche in epoche precedenti:

Babilonesi 2000 a.c.	Nei testi babilonesi si trovano numerosi esempi di equazioni di 3° grado. Equazioni del tipo  venivano risolte consultando direttamente le tavole dei cubi e delle radici cubiche.
Greci	Nelle opere greche si trovano solo rari esempi di problemi di 3° grado. Problemi tratti dalla geometria li troviamo risolti sia da Archimede (III secolo a.C.) sia da Diofanto (III secolo d.C.).
Arabi Intorno al 1000 d.C.	I primi esempi di equazioni di 4° grado si trovano in alcune opere arabe.
Dal X al XII secolo	A questo periodo risalgono i lavori di diversi autori, tra i quali anche Leonardo Fibonacci, sulla risoluzione di particolari equazioni di 3° grado.
Nel XVI secolo	Agli inizi del XVI secolo diversi matematici italiani (Dal Ferro, Tartaglia, Cardano) contribuirono, ognuno indipendentemente dagli altri, alla risoluzione mediante la formula delle equazioni di 3° grado. Sempre nella metà del 1500 si arriva alla formula risolutiva delle equazioni di 4° grado grazie al contributo di Ludovico Ferrari.

A Scipione Dal Ferro ( 1515 ) dobbiamo la formula risolutiva per l’equazione
.
Successivamente Gerolamo Cardano, studiando le trasformazioni che permettono di ridurre un’equazione in un’altra di più facile risoluzione, trovò quella che riduce l’equazione di 3° grado completa

a quella di Dal Ferro
,
che risolse con la formula di quest’ultimo.
Sempre nel 1500, Ludovico Ferrari trovò la formula risolutiva valida per le equazioni di 4° grado.
Il trattato che divulgò i nuovi definitivi risultati fu scritto da Cardano e pubblicato con il titolo “Ars Magna” nel 1545.

Con questi risultati, si era in grado di affermare che le equazioni di grado minore o uguale al 4° hanno in comune la proprietà di essere tutte risolubili “per radicali”.
Naturalmente, dopo i risultati ottenuti nel XVI sec., le ricerche continuarono nel tentativo di ottenere metodi algebrici con cui risolvere anche equazioni generali di grado superiore al quarto. Questi tentativi si prolungarono nei secoli XVII e XVIII, senza mai riuscire nello scopo. Lagrange, nella sua opera “Reflexions sur la resolution algebrique des equations”, del 1770, mette in evidenza il fatto che i metodi validi per le equazioni fino al 4° grado non danno esito positivo per quelle di grado superiore. Lagrange afferma che:
“il problema di risolvere per radicali equazioni il cui grado è superiore al 4°, è uno di quelli che non è possibile risolvere, anche se nulla dimostra l’impossibilità di tale soluzione”.

Tra la fine del XVIII secolo e l’inizio del XIX, il problema principale dell’algebra era quello di “trovare una formula risolutiva per un’equazione algebrica completa di grado n in un’ incognita”.
J. L. Lagrange ( ), nell’opera “Traité de la résolution des équations numériques de tous les degrés” del 1808 scrive:
“La soluzione di un problema è ridotta in ultima analisi alla risoluzione di una o più equazioni, con coefficienti numerici, dette appunto equazioni numeriche. Quindi è molto importante avere dei metodi per risolvere completamente queste equazioni, di un certo grado ...”
però
 “... Bisogna distinguere la risoluzione delle equazioni numeriche da quello che in Algebra si chiama la risoluzione generale delle equazioni. La prima è una operazione aritmetica, fondata sui principi generali della teoria delle equazioni, ma i risultati non sono altro che dei numeri ...”
mentre
“... Il carattere essenziale dell’Algebra è che i risultati delle operazioni non danno i valori delle quantità che cerchiamo, ma rappresentano solo le operazioni che fatte sulla quantità iniziale data fanno ottenere i valori cercati ...”
infatti
“... L’algebra, come la si intende comunemente, è l’arte di determinare quantità incognite in quanto funzioni di quantità conosciute o supposte tali; è altresì l’arte di trovare una soluzione generale per equazioni. Questa soluzione consiste nel ricercare per tutte le equazioni dello stesso grado, quelle funzioni dei coefficienti delle equazioni stesse che ne rappresentano tutte le radici. Finora il problema si può considerare risolto solo per equazioni di 1°, 2°, 3°, e 4° grado ...”.

La questione della risolubilità per radicali fu finalmente chiarita all’inizio del XIX sec. dai matematici P. Ruffini (nel 1799) e N.H. Abel (nel 1824) i quali dimostrarono, indipendentemente l’uno dall’altro, che “una equazione di grado superiore al 4° non è risolubile per radicali”.

Equazioni binomie
Nel periodo in cui la maggior parte dei matematici cercava di risolvere per radicali l’equazione generale di grado n, molti di loro si dedicarono allo studio dell’equazione binomia
     
dove n è un numero naturale non nullo e a un numero reale.
La risoluzione di una tale equazione comporta il calcolo delle radici n-esime di a.
A questo punto, anche partendo da degli esempi numerici, possiamo chiedere alla classe se c’è qualche osservazione da fare a seconda se n è un numero pari o dispari, facendo risolvere agli alunni le seguenti equazioni:

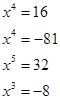
Quindi si può far notare agli alunni che, dal momento che esiste un numero infinito di equazioni di grado superiore al 4° risolubili per radicali, basti pensare a quelle del tipo
 con ,
dopo i risultati di Ruffini e Abel, rimaneva aperto il problema fondamentale di caratterizzare le equazioni algebriche di grado n risolubili per radicali, cioè andava risolta la questione di trovare tutti i tipi di equazioni che si risolvono per radicali.
Il problema fu risolto da Galois, che nel 1830-31 per primo applicò alla teoria delle equazioni dei concetti nuovi, che nel moderno linguaggio formano la Teoria dei gruppi e dei campi. Il discorso porterebbe a notevoli approfondimenti che però non sono oggetto di tale trattazione. Per il lavoro che deve essere svolto insieme alla classe è sufficiente sapere che il problema legato alla risolubilità per radicali delle equazioni ha portato, con il tempo, allo sviluppo dell’algebra moderna.

Equazioni biquadratiche
Alcune equazioni possono essere risolte usando il metodo del cambiamento di variabile, vediamo in cosa consiste attraverso una sua applicazione.
Le equazioni di 4° grado, come sappiamo, possono essere scritte nella forma  dove  è un polinomio di 4° grado. Nel caso in cui, all’interno del polinomio, siano nulli i coefficienti dei termini di 3° e 1° grado l’equazione assume la seguente forma

ed in questo caso si parla di equazioni biquadratiche. Come possono essere risolte? Possiamo lasciare alla classe il tempo di provare e tentare delle ipotesi. Si potrebbe porre  (cambiamento di variabile), così avremo l’equazione di 2° grado nell’incognita t

di facile risoluzione. Se tale equazione ammette le due soluzioni  e  possiamo ricavare la nostra incognita x risolvendo le due equazioni di 2° grado

Interpretazione grafica delle soluzioni di un’equazione di 3° grado ad un’incognita con Derive
Prendendo l’equazione risolvente del problema della vasca, proposto in precedenza

consideriamo la scrittura
.
Con la classe possiamo provare a tracciare in modo approssimato il grafico della curva che ha questa come equazione. A questo punto del lavoro i ragazzi non dovrebbero avere problemi a capire che le soluzioni dell’equazione non sono altro che le ascisse dei punti di intersezione tra la curva e l’asse delle x.
Per ottenere un grafico più accurato ci possiamo aiutare con Derive:

4 Esempi di verifiche

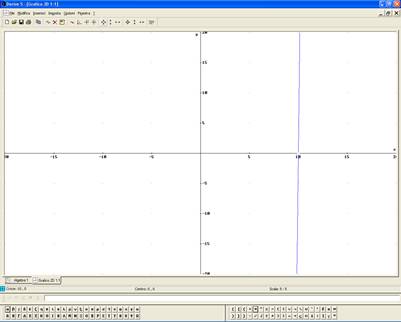
Una possibile Verifica di fine Unità, potrebbe essere organizzata secondo il seguente schema, valido per ciascuna delle unità didattiche presentate:
Esercizi di verifica delle conoscenze:

• tradurre in equazioni domande espresse in frase e viceversa
• saper tradurre una situazione problematica in un’equazione, quindi saper passare dalla formulazione del problema alla scrittura dell’equazione
• stabilire quale tra più equazioni proposte è l’equazione risolvente del problema dato
• saper dare un’interpretazione geometrica della risoluzione di un’equazione
• saper rispondere a domande del tipo “Che cosa significa risolvere un’equazione? Come sono tra loro gli insiemi soluzione di equazioni equivalenti?”
• conoscere i procedimenti di risoluzione di equazioni e i criteri per definire il campo di validità delle soluzioni
• saper riconoscere equazioni impossibili e indeterminate
• saper distinguere il ruolo dell’incognita da quello dei parametri nelle equazioni letterali.

Esercizi di verifica delle competenze operative:

• risolvere e discutere equazioni razionali numeriche e letterali intere e fratte
• interpretare graficamente nel piano cartesiano le soluzioni di un’equazione
• risolvere particolari equazioni mediante la Legge dell’annullamento del prodotto.
• Impostare e risolvere problemi di varia natura mediante l’uso di modelli matematici basati sulle equazioni algebriche. In questa fase lo studente deve precisare quale grandezza viene indicata con x, scrivere l’equazione risolvente, risolverla e stabilire quale/i delle soluzioni ottenute è/sono accettabile/i
• individuare le conseguenze, utili nel calcolo, dei Principi di equivalenza (se in un’equazione si trasporta un addendo da un membro all’altro cambiandolo di segno, si ottiene un’equazione equivalente alla data oppure, cambiando i segni a tutti i termini di un’equazione si ottiene un’equazione equivalente alla data).

Verifica del processo di apprendimento, utile anche per un’eventuale azione di recupero
Si possono porre le seguenti domande

• A cosa servono le equazioni? In quali contesti pensi possano essere utili?
• Di fronte ad un problema, a cosa pensi? Quali sensazioni provi?
• Credi di aver acquisito un metodo o una strategia per risolvere certi tipi di problemi?

Esempio di Verifica sull’Unità didattica “Equazioni algebriche di 1° grado ad un’incognita”

• Per quali valori di a i polinomi  e  assumono lo stesso valore?
• Traduci in frasi le seguenti uguaglianze tra espressioni algebriche, dove n rappresenta un numero naturale:
• 
• 
• 
• 
• Dai la definizione di radice di un’equazione numerica.
• Indica quale delle seguenti definizioni è esatta:
• Due equazioni si dicono equivalenti se alcune soluzioni dell’una sono anche soluzioni dell’altra                              ¨
• Due equazioni si dicono equivalenti se tutte le soluzioni della prima sono anche soluzioni della seconda                   ¨
• Due equazioni si dicono equivalenti se tutte le soluzioni della prima sono anche soluzioni della seconda e viceversa ¨
• Alberto vuole convincere il suo compagno di banco che “” e gli presenta un foglio su cui ha scritto le seguenti frasi:

Si sa che  (con )

• moltiplico per  a sinistra e a destra del simbolo di uguale e ottengo
• aggiungo  ad entranbe le parti e ottengo
• scomponendo in fattori ottengo
• divido a destra e a sinistra per  e ottengo
• siccome avevo che  posso scrivere  al posto di e ottengo
• eseguendo l’addizione ottengo
• dividendo per  ottengo .

Come è possibile?

• Indica per quali valori numerici le seguenti equazioni “perdono significato”
• 
• 
• Risolvi e discuti le seguenti equazioni:
• 
• 
• 
• 
• Trova il valore di k per cui l’equazione
• ha per soluzione
• ha per soluzione
• è impossibile
• Due amici, Gianni e Alberto, si recano in una libreria e acquistano complessivamente 5 libri. Alberto compera un libro da 35 euro, uno da 20,5 euro e uno 10,5 euro. Gianni sceglie un libro da 28 euro e uno da 16 euro. Alberto, avendo ottenuto uno sconto, paga per entrambi la somma di 100 euro. Si chiede quale somma Alberto deve farsi restituire da Gianni, nel caso voglia ripartire lo sconto in parti proporzionali alla spesa complessiva di ognuno.

E’ richiesto di:

• Impostare uno o più piani di lavoro indicando i dati necessari, le informazioni che si possono dedurre dai dati, l’elemento da trovare (l’incognita);
• Risolvere;
• Controllare se la soluzione trovata è “ragionevole”.
• In un supermercato in un giorno sono state vendute 20 paia di guanti, alcuni di lana del costo di 25 euro, gli altri di pelle del costo di 37,5 euro. L’incasso globale è stato di 687,5 euro. Quanti erano i guanti di lana e quanti quelli di pelle?

Tempo di svolgimento: circa 2h	Punteggio totale: 12 (10/10)
Esercizio n.1	1
Esercizio n.2	1
Esercizio n.3	0.5
Esercizio n.4	0.5
Esercizio n.5	1
Esercizio n.6	1
Esercizio n.7	2
Esercizio n.8	1
Esercizio n.9	2.5
Esercizio n.10	1.5

Esempio di Verifica sull’Unità didattica “Equazioni algebriche di 2° grado e di grado superiore, ad un’incognita”

• Come sono le radici di un’equazione di 2° grado quando il suo discriminante è nullo?
• Quando è conveniente applicare la cosiddetta formula ridotta? Come si ricava?
• Dai la definizione di radice di un’equazione numerica.
• Indica per quali valori numerici le seguenti equazioni “perdono significato”
• 
• 
• Risolvi e discuti le seguenti equazioni, dove è possibile senza l’uso della Formula risolutiva:
• 
• 
• 
• 
• 
• 
• Nell’equazione  determinare k in modo che
• esistano le due soluzioni  e siano distinte
• 
• 
• le due soluzioni siano coincidenti
• Un rettangolo ha il perimetro di 80 cm e la base di 26 cm. Determinare i lati di un secondo rettangolo interno al dato, con i lati equidistanti dai lati del primo, e di area 28 cm².
• Determinare le lunghezze dei lati di un trapezio rettangolo, di area , sapendo che la diagonale minore è lunga  e che l’altezza supera di  la base minore.
• Risolvi e discuti le seguenti equazioni:
• 
• 
• 
• 
• 
• 
• Trovare tre numeri interi consecutivi sapendo che il loro prodotto è 990.

 

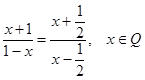
Tempo di svolgimento: circa 2h	Punteggio totale: 14 (10/10)
Esercizio n.1	0.5
Esercizio n.2	0.5
Esercizio n.3	0.5
Esercizio n.4	0.5
Esercizio n.5	2.5
Esercizio n.6	1.5
Esercizio n.7	2
Esercizio n.8	2
Esercizio n.9	2.5
Esercizio n.10	1.5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Bibliografia

 

• C. B. Boyer   “Storia della matematica”  - Mondadori
• R. Franci - L. Toti Rigatelli   “Storia della teoria delle equazioni algebriche”  - Mursia
• L. Tonolini - F. Tonolini - A. Manenti Calvi   “Fondamenti e metodi di matematica” – Volume “Laboratorio di matematica con l’Informatica” - Minerva Italica
• N. Dodero - P. Baroncini - R. Manfredi   “Lineamenti di matematica” - Vol.1 - Ghisetti e Corvi

Fonte: http://www.itis.arezzo.it/index.php?option=com_docman&task=doc_download&gid=1169&Itemid=115

Sito web da visitare: http://www.itis.arezzo.it/

Autore del testo: Katia Comandi

Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.

 

Equazioni

 

 

I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

Equazioni

 

"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco

www.riassuntini.com dove ritrovare l'informazione quando questa serve