I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
La goniometria è la parte della matematica che si occupa dello studio degli angoli.
1. Angoli e loro misure
Date in un piano due semirette a,b di origine o si definisce angolo ciascuna delle due parti del piano delimitate dalle due semirette.
Il punto o si dice vertice dell’angolo e le due semirette lati dell’angolo.
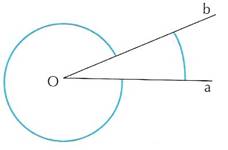
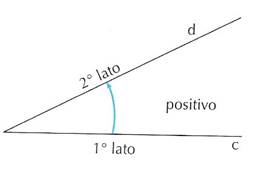
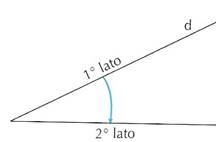Un angolo si dice orientato quando si stabilisce quale dei due lati è il primo e quale il secondo.
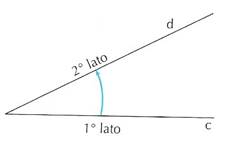
Un angolo orientato di lati a, b può anche essere generato dalla rotazione del primo lato dell’angolo fino a sovrapporsi al secondo lato.
Per convenzione, si considera positivo un angolo che si ottiene con una rotazione antioraria, negativo un angolo che si ottiene con una rotazione oraria.
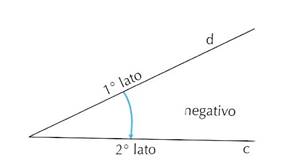
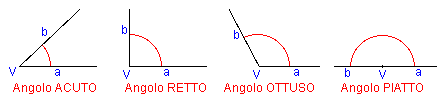
Si definisce angolo retto un angolo che compie esattamente un quarto di giro attorno al proprio vertice; un angolo piatto compie mezzo giro ed un angolo giro compie un giro completo.
Si definisce inoltre acuto un angolo minore di un angolo retto ed ottuso un angolo maggiore di un angolo retto.
L’unità di misura comunemente usata per gli angoli è il grado. Un grado (1°) si definisce come la 360a parte di un angolo giro.
Di conseguenza un angolo giro misura 360°, un angolo piatto 180° e un angolo retto 90°.
La sessantesima parte del grado si chiama minuto primo (1’) e la sessantesima parte del minuto primo si chiama minuto secondo (1’’). In formule:
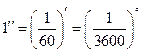
Un altro modo di misurare gli angoli è quello di assumere come unità di misura il radiante. La misura in radianti di un angolo orientato si calcola come il rapporto tra l’arco che i lati dell’angolo staccano sopra una qualsiasi circonferenza di centro o, ed il raggio della circonferenza.
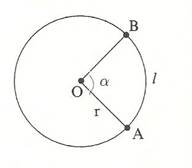
La misura di 
in radianti è uguale al rapporto tra l’arco AB
ed il raggio: 
Ricordando che la lunghezza di una circonferenza di raggio r è 
, si possono calcolare facilmente le misura in radianti degli angoli giro, piatto e retto.
misura dell’angolo giro in radianti: 
misura dell’angolo piatto in radianti: 
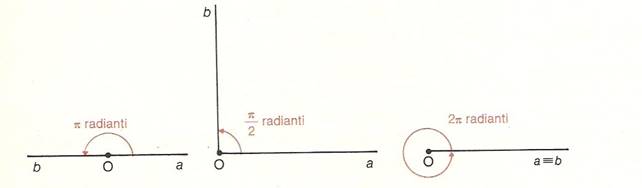misura dell’angolo retto in radianti: 
Vogliamo ora determinare la relazione tra le misure in gradi ed in radianti di uno stesso angolo.
Se un angolo misura 
per ottenere l’equivalente misura in radianti 
basta applicare la proporzione
da cui ricavo
Viceversa se si vuole sapere la misura in gradi di un angolo che misura 
dalla stessa proporzione
ricavo
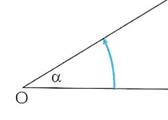
Consideriamo l’angolo 
di lati a, b e di vertice o. Tale angolo è descritto dalla rotazione del primo lato a sul secondo lato b.
b
a
Osserviamo che il lato a può sovrapporsi al lato b anche dopo aver descritto un numero qualsiasi di angoli giri.
Gli angoli che si ottengono da un angolo 
sommato ad un certo numero di angoli giri, si chiamano angoli impropri.
In generale, se 
è l’ampiezza di un angolo di lati a e b, tutti gli angoli aventi gli stessi lati, espressi in gradi, sono:
dove k è un intero relativo che indica il numero di giri completi che la semiretta a compie attorno al vertice o dopo aver descritto l’angolo di ampiezza 
. L’intero k è positivo o negativo a seconda che la semiretta a compia i giri completi in senso antiorario o in senso orario.
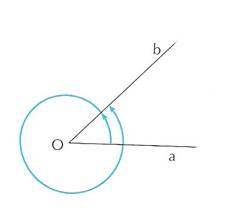
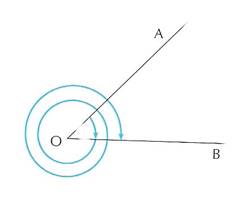
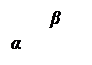
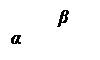
Figura 2
Figura 1
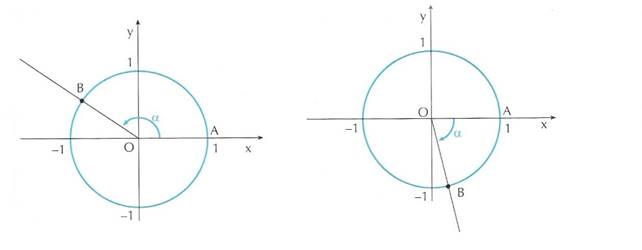
In figura 1 l’angolo 
è ottenuto dall’angolo 
più un giro completo in senso antiorario, quindi: 
.
In figura 2 l’angolo 
è ottenuto dall’angolo 
più due giri completi in senso orario, quindi: 
.
2. Funzioni goniometriche
2.1 La circonferenza goniometrica
Consideriamo in un piano cartesiano xOy la circonferenza con il centro nell’origine e raggio pari all’unità. Tale circonferenza sarà chiamata d’ora in poi circonferenza goniometrica.
Sia dato un angolo orientato 
. Disponiamo tale angolo nel piano cartesiano nel seguente modo: facciamo coincidere il vertice dell’angolo con l’origine O del sistema di riferimento e il suo primo lato con il raggio OA. Sia B il punto in cui il secondo lato dell’angolo interseca la circonferenza. Qualunque sia l’angolo 
il punto A viene a trovarsi sempre nella stessa posizione e quindi ha sempre le stesse coordinate: A(1,0); la posizione di B invece, dipende dall’angolo scelto. Chiamiamo B il punto associato all’angolo 
sulla circonferenza goniometrica.
In figura 3 sono riportati i punti associati agli angoli particolari. Il punto A è associato all’angolo di 0° e anche all’angolo di 360°; il punto B è associato all’angolo retto; il punto C all’angolo piatto; il punto D è associato all’angolo di 270°.
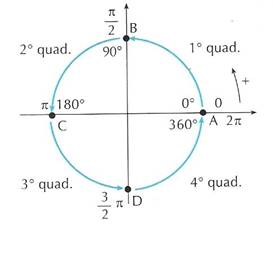
Figura 3
2.2 Seno e coseno di un angolo
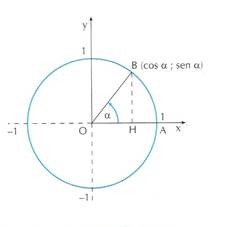
Si dice seno di un angolo 
l’ordinata del punto associato ad 
nella circonferenza goniometrica. (in figura il seno di 
è BH)
Si dice coseno di un angolo 
l’ascissa del punto associato ad 
nella circonferenza goniometrica. (in figura il coseno di 
è OH)
Consideriamo adesso l’angolo 
di figura 4 e supponiamo che il punto P si muova sulla circonferenza in modo che l’angolo 
assuma tutti i valori possibili tra 0° e 360°.
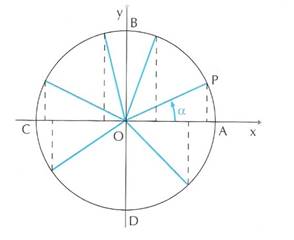
Figura 4
Quando 
, cioè 
, l’ordinata di P è zero e l’ascissa di P è uno, quindi si avrà:
; 
.
Se P si sposta da A a B nel primo quadrante, cioè 
cresce da 0° a 90°, l’ordinata di P è positiva, cioè 
, e cresce da 0 a 1, mentre l’ascissa di P è positiva, cioè 
, ma decresce da 1 a 0.
Si avrà poi quando 
; 
.
Sempre osservando la figura 4 e ripetendo le stesse considerazioni, si ottiene che al crescere di 
da 90° a 180°, nel secondo quadrante, è 
e 
decresce da 1 a 0, mentre 
e 
decresce da 0 a –1.
Quando 
si ha
; 
.
Al crescere di 
da 180° a 270° nel terzo quadrante, il seno decresce da 0 a –1 ed è negativo, mentre il coseno cresce da – 1 a 0 ed è negativo.
Quando 
si avrà
; 
.
Al crescere di 
da 270° a 360°, nel quarto quadrante, il seno cresce da – 1 a 0 ed è negativo, mentre il coseno cresce da 0 a 1 ed è positivo.
A questo punto, quando P torna in A, si ha
; 
.
Crescendo 
oltre 360° i valori del seno e del coseno si ripetono periodicamente; diremo quindi che il seno ed il coseno sono funzioni periodiche con periodo uguale a 360° e si scrive:
; 
.
dove k è un qualsiasi numero intero positivo o negativo.
Se per misurare l’angolo 
si utilizzano i radianti, si scrive:
; 
.
2.3 Tangente di un angolo
Sia dato un angolo 
; costruiamo al solito modo la circonferenza goniometrica e conduciamo dal punto A la retta t tangente alla circonferenza. Sia T il punto in cui il secondo lato dell’angolo, o il suo prolungamento, incontra tale tangente.
In figura si vede come cambia la situazione se 
appartiene al primo, secondo, terzo, o quarto quadrante.
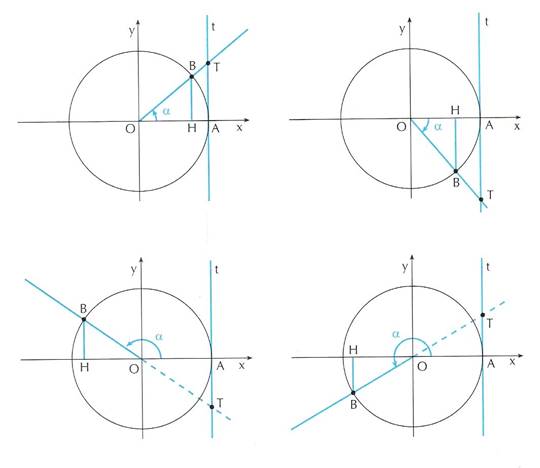
La tangente di un angolo orientato è l’ordinata del punto di intersezione tra il secondo lato dell’angolo, o il suo prolungamento, con la retta tangente alla circonferenza goniometrica nel punto A.
Si osservi che se il secondo lato dell’angolo 
viene a cadere sull’asse y, tale lato risulta parallelo alla retta t, e quindi non può mai intersecarla.
Perciò se 
, la tangente di 
non esiste.
Mentre se 
, il punto T coincide con il punto A, pertanto la sua ordinata è zero. Risulta quindi
Anche per 
il punto T coincide con A, quindi
Anche la tangente, come il seno ed il coseno, è una funzione periodica, ma stavolta il periodo non è un angolo giro, ma un angolo piatto. La tangente di un angolo, cioè, assume gli stessi valori ogni 180°. Scriveremo quindi
oppure 
2.4 Relazioni fondamentali della goniometria
Consideriamo una circonferenza goniometrica e un angolo orientato 
.
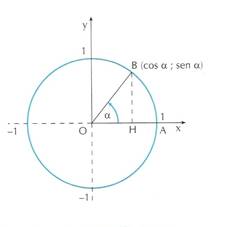
Consideriamo il triangolo rettangolo di vertici BOH: I cateti BH e OH sono rispettivamente il seno ed il coseno dell’angolo 
, mentre l’ipotenusa OB è il raggio della circonferenza.
Applicando il teorema di Pitagora al triangolo sopra descritto si ha:
, cioè
.
La somma dei quadrati del seno e del coseno di uno stesso angolo è uguale all’unità. Questa è la prima relazione fondamentale della goniometria.
Consideriamo adesso anche la tangente dall’angolo 
, AT
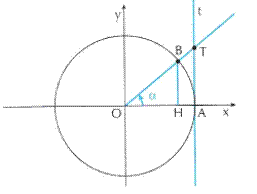
e consideriamo i due triangoli rettangoli BOH e TOA. Questi triangoli hanno i tre angoli in comune e sono quindi simili. Allora possiamo mettere in proporzione i loro lati. Otteniamo così:
, cioè
Da quest’ultima proporzione ricaviamo la tangente di 
:
Tale formula si chiama seconda relazione fondamentale della goniometria.
2.5 Cotangente di un angolo
Si usa talvolta un’altra funzione goniometrica, che si chiama cotangente di un angolo e si definisce come il reciproco della tangente:
Questa formula ha significato purché la tangente di 
esista e sia diversa da zero, cioè deve essere 
. Ricordando la seconda relazione fondamentale della goniometrica, si avrà:
.
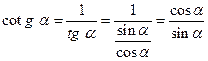2.6 Grafici delle funzioni goniometriche
È facile costruire il grafico delle funzioni rappresentate dalle equazioni
Basta portare sull’asse delle ascisse le misure dell’angolo espresse in radianti e sull’asse delle ordinate i corrispondenti valori del seno, del coseno e della tangente. Le curve che così si ottengono vengono dette, rispettivamente, sinusoide, cosinusoide, tangentoide.
Sinusoide
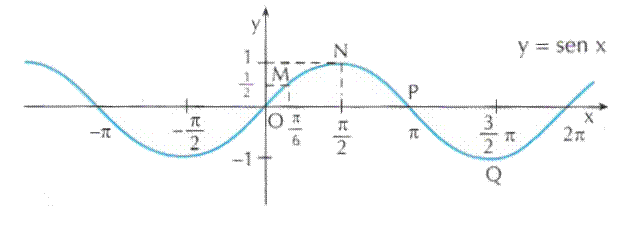
Cosinusoide
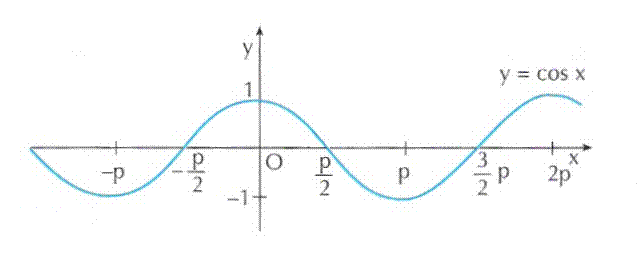
Tangentoide
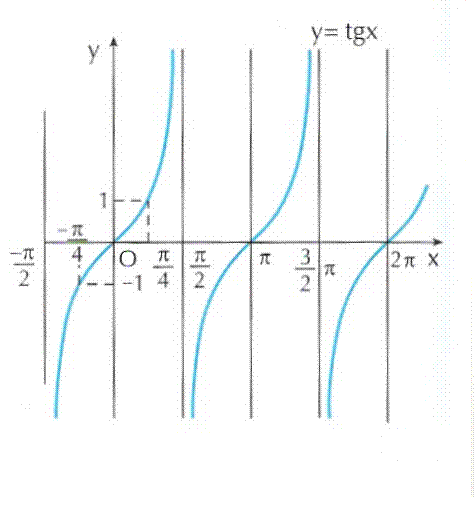
2.7 Funzioni goniometriche inverse
Nel paragrafo precedente abbiamo considerato la funzione 
, che ad ogni valore dell’angolo x, associa il corrispondente valore del seno.
Vogliamo costruire la funzione inversa, cioè la funzione che, dato un valore del seno associa il corrispondente valore dell’angolo. Tale funzione si chiama arcoseno e si scrive
che significa “x è l’angolo il cui seno è y”. Si conviene però di assumere per x solo gli angoli compresi tra 
e 
, cioè 
.
Analogamente si può definire la funzione inversa della funzione 
, se si considerano solo angoli appartenenti all’intervallo chiuso 
. Essa si chiama arcocoseno e si scrive
che significa “x è l’angolo il cui coseno è y”.
In modo analogo dalla funzione 
, se si considerano solo angoli appartenenti all’intervallo aperto 
, si può ricavare la funzione inversa. Tale funzione si chiama arcotangente e si scrive
che significa “x è l’angolo la cui tangente è y”.
Esempio: calcoliamo il valore di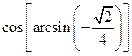 
.
Poniamo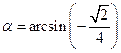 
. Vogliamo dunque calcolare il coseno di un angolo 
sapendo che il seno è 
. Possiamo applicare la prima equazione fondamentale della goniometria e otteniamo:
.
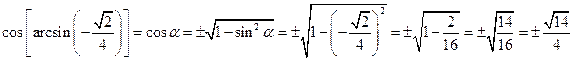Per quanto si è detto prima però la funzione arcoseno è definita soltanto per angoli 
, e per tali angoli il coseno è positivo, quindi tra i due valori 
dobbiamo prendere solo quello positivo. In definitiva abbiamo
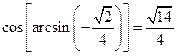
2.8 Relazioni tra particolari coppie di angoli
2.8.1 Angoli associati
Si costruisca al solito modo una circonferenza goniometrica e si consideri un angolo orientato 
come in figura. Sia B il punto della circonferenza goniometrica associato ad 
. Dal punto B si conduca la parallela all’asse delle ascisse e sia 
il punto in cui tale parallela incontra la circonferenza; si conducano poi i diametri 
e 
. Risultano in tal modo individuati gli angoli
che si chiamano angoli associati all’angolo dato 
.
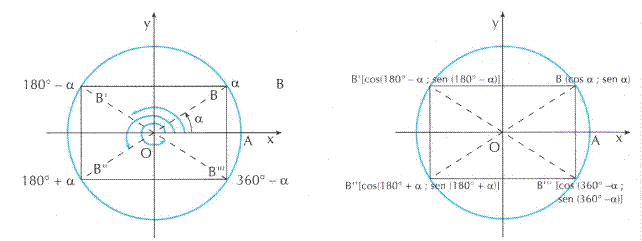
Vogliamo determinare il sono, il coseno e la tangente degli angoli associati ad 
. Analizzando la figura si ha:
e 
e 
e 
2.8.2 Angoli opposti
Due angoli si dicono opposti se la loro somma è zero.
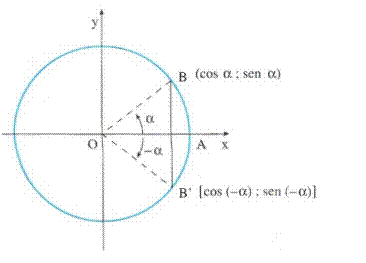
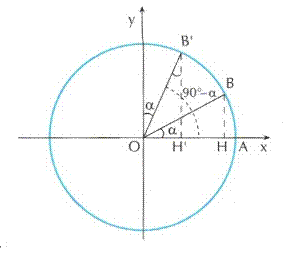
Tali angoli possono essere considerati come due angoli orientati in senso opposto e la cui ampiezza è uguale in valore assoluto. I loro rispettivi punti associati sulla circonferenza goniometrica B e B coincidono con i punti associati a due angoli esplementari. Si avrà allora:
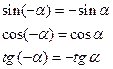
2.8.3 Angoli complementari
Due angoli si dicono complementari se la loro somma è 90°. Consideriamo in figura gli angoli 
e 
.
I triangoli OBH e 
sono congruenti poiché sono rettangoli in H e 
, hanno 
e 
. I lati corrispondenti in triangoli congruenti sono congruenti, quindi si avrà:
Si avrà poi:
Fonte: http://www.varieties.altervista.org/Goniometria.doc
Sito web da visitare: http://www.varieties.altervista.org
Autore del testo: non indicato nel documento di origine
Il testo è di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente i loro testi per finalità illustrative e didattiche. Se siete gli autori del testo e siete interessati a richiedere la rimozione del testo o l'inserimento di altre informazioni inviateci un e-mail dopo le opportune verifiche soddisferemo la vostra richiesta nel più breve tempo possibile.
I riassunti , gli appunti i testi contenuti nel nostro sito sono messi a disposizione gratuitamente con finalità illustrative didattiche, scientifiche, a carattere sociale, civile e culturale a tutti i possibili interessati secondo il concetto del fair use e con l' obiettivo del rispetto della direttiva europea 2001/29/CE e dell' art. 70 della legge 633/1941 sul diritto d'autore
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
"Ciò che sappiamo è una goccia, ciò che ignoriamo un oceano!" Isaac Newton. Essendo impossibile tenere a mente l'enorme quantità di informazioni, l'importante è sapere dove ritrovare l'informazione quando questa serve. U. Eco
www.riassuntini.com dove ritrovare l'informazione quando questa serve