Los resúmenes, toma nota de los textos que figuran en nuestra página web se ponen a disposición de forma gratuita con fines didácticos de la ilustración, científica, social, civil y cultural a todos los posibles interesados de acuerdo con el concepto de uso justo, y con el 'objetivo de cumplimiento de la Directiva Europea 2001/29 / CE y del «arte. 70 de la ley 633/1941 sobre derechos de autor
La información médica y de la salud en este sitio es de carácter general y para propósitos informativos solamente y por lo tanto no puede en ningún caso sustituir el consejo de un médico (o un autorizado legalmente a la profesión).
Introducción
La mayoría de los circuitos son una combinación de tensiones y cargas, que le permiten a las corrientes utilizar diversos métodos de funcionamiento en el circuito. La complejidad del circuito realmente no interesa, pues cada circuito individual seguirá las leyes de la teoría fundamental. El comprender estas teorías nos ayudará a analizar y a conocer las condiciones de trabajo de los diferentes circuitos bajo diversas condiciones.
A todos los circuitos se les suministra energía de una corriente directa (CD, DC) o de una fuente alterna (CA, AC). A pesar de que hay diferencias básicas entre circuitos AC y DC, es correcto usar las teorías, reglas y definiciones de un circuito DC para otro de AC. Por lo tanto, en este capítulo
explicaremos el concepto de un circuito en serie que trabaja con una fuente de CD, así como para explicar la Ley de Kirchhoff de la Tensión (Voltaje), llamada KVL y la regla de división de la tensión.
Si ambos terminales en sendos dispositivos se conectan a una unión común y no existe ningún otro dispositivo con corriente conectado a esta unión, la conexión se conoce como una serie. En la Fig. 3.1 están conectadas dos resistencias R1 y R2 a una única unión, por lo que se considera que están en serie.
Unión
única
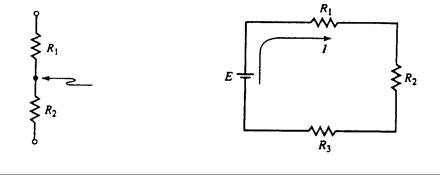
Fig. 3.1 – Resistencias en serie Fig. 3.2 – Circuito en serie
En la Fig. 3.2, el suministro de tensión y las tres resistencias están conectadas en serie. La corriente sale del terminal positivo de la fuente de potencia y pasa a través de las tres resistencias, para regresar luego al terminal negativo de la fuente.
En este circuito podemos ver que la fuente de tensión E está conectada en serie a la resistencia R1, que ésta está conectada en serie con la resistencia R2, que a su vez está conectada en serie con la resistencia R3 y finalmente ésta está en serie con la fuente de tensión E. Esto constituye un circuito en serie.
Hay una característica importante en este circuito en serie: la corriente que entra en un dispositivo es igual a la corriente que sale del mismo. La razón para esto es que no hay pérdida de corriente en ninguna de las uniones, por lo que tenemos que:
La corriente que pasa a través de un dispositivo en un circuito en serie es siempre la misma
Este enunciado nos ayudará a comprender los circuitos en serie y sus características.
La Ley de la Tensión (Voltaje) de Kirchhoff es de mucha importancia en circuitos electrónicos. Se define como que: En un circuito o lazo cerrado, la suma algebraica del aumento de potencial y de la disminución de potencial o tensión es siempre igual a cero, lo que matemáticamente se expresa como:
SV = 0 para un lazo cerrado (3.1)
En esta ecuación, la letra griega S significa ”suma”, y la letra V significa la tensión o potencial en aumento o en disminución. El lazo cerrado consiste en tomar un punto fijo como partida, atravesar todo el circuito y regresar en la dirección opuesta al punto original de salida.
Existe otra definición para la Ley de la Tensión de Kirchhoff, que enuncia que: La suma del potencial en aumento es igual a la suma del potencial en disminución que atraviesa el circuito cerrado, es decir:
SAum =SDism para un lazo cerrado (3.2)
En el circuito de la Fig. 3.3, tomemos el punto w como inicio y recorramos el circuito I con la dirección de la corriente. Al pasar por la fuente de potencial E hay un aumento de tensión entre el punto w y el punto x. Nos movemos luego del punto x al punto y y pasamos por la resistencia Ra, donde hay una caída de tensión Va. Al pasar por las resistencias Rb y Rc hay caídas de potencial Vb y Vc. Utilizando la Ley de la Tensión de Kirchhoff en un circuito cerrado, obtenemos la siguiente expresión matemática:
E – Va – Vb – Vc = 0

Podemos seleccionar cualquier dirección para la corriente al escribir la Ley de las Tensiones de Kirchhoff. Si seguimos la ruta wzyxw (opuesta a la dirección de la corriente) para atravesar el circuito, obtenemos:
Vc + Vb + Va – E = 0
Estas dos ecuaciones se pueden verificar mediante un cálculo simple.
Ejemplo 3.1: En la Fig. 3.4 verifique la Ley de las Tensiones de Kirchhoff.
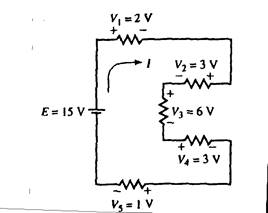
Fig. 3.4
Respuesta: Escriba la ecuación siguiendo la dirección de la corriente:
15V – 2V – 3V – 6V – 3v – 1V = 0
Es posible simplificar todos los circuitos complejos. Con un ejemplo podemos explicar la manera de simplificar un circuito con una fuente de tensión y varias resistencias en serie. Véase el circuito de la Fig. 3.5
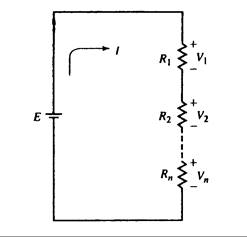
Fig. 3.5
En vista de que el circuito es una trayectoria cerrada (lazo), la fuente de tensión producirá corriente en el circuito. Esta corriente creará una caída de tensión en cada una de las resistencias, ya que:
Vx = I x Rx
Aplicando la Ley de Kirchhoff de las Tensiones en el circuito cerrado, tenemos que:
E = V1 + V2 + ... + Vn
E = IR1 + IR2 + ... + IRn
E = I (R1 + R2 + ... + Rn)
Si reemplazamos todas las resistencias por una sola equivalente RT, el circuito será como el que se muestra en la Fig. 3.6.
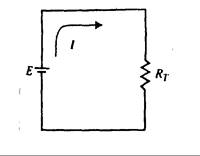
Fig. 3.6
Usando la Ley de Ohm obtenemos que:
E = IRT (3.3)
El circuito en la Fig. 3.5 es equivalente al de la Fig. 3.6, por lo que podemos concluir que: Si hay n resistencias en serie, entonces la resistencia total será igual a :
RT = R1 + R2 + ... + R n-1 + Rn (Ohmios, W) (3.4)
Si estas n resistencias tienen todas el mismo valor, entonces la resistencia total será:
RT = nR (Ohmios, W) (3.5)
Ejemplo: Determine la resistencia total del circuito en la Fig. 3.7
Respuesta:
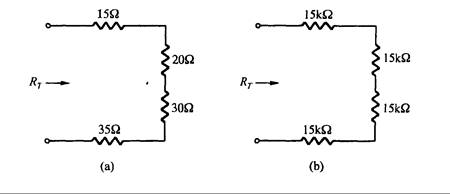
Fig. 3.7
Cualquier fuente de tensión conectada a los terminales primero y último de una resistencia en serie tendrá el mismo efecto que conectar los dos terminales de la resistencia RT y se obtendrá la misma corriente. De la Ley de Ohm se tiene que:
I = E / R (Amperios, A) (3.6)
La potencia de disipación para cada resistencia es:
Pn = I n2 Rn (Watts, W) (3.7)
Al usar la resistencia equivalente RT para reemplazar, la potencia es:
PT = E I (Watts) (3.8)
Debido a la ley de conservación de la energía, la suma de la energía disipada por cada resistencia es igual a la potencia suministrada por la fuente, y
PT = P1 + P2 + P3 + ... + Pn (Watts) (3.9)
Ejemplo 3.3: Determine los valores siguientes para el circuito de la Fig. 3.8:
Fig. 3.8
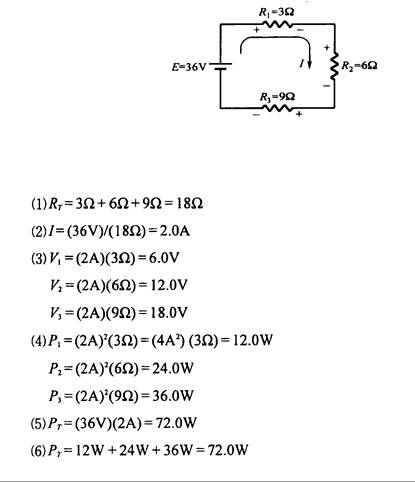
Si en un circuito en serie existen muchas fuentes de tensión, se pueden reemplazar por una única fuente de tensión equivalente. El valor de esta fuente es igual a la suma de estas fuentes individuales de tensión. Tales fuentes individuales tienen también diferentes direcciones de conexión, por lo que es necesario tomar en cuenta la dirección de la conexión de cada una de ellas para poder determinar la magnitud y polaridad de la fuente equivalente.
Si todas estas fuentes de tensión están conectadas en la dirección en que aumenta el potencial, entonces la magnitud de la fuente de tensión equivalente es igual a la suma de todas las fuentes de tensión, como se muestra en la Fig. 3.9.

Fig. 3.9
Si las fuentes de tensión no están conectadas todas en la misma dirección, entonces la magnitud de la fuente equivalente de tensión es igual a la diferencia entre fuentes de tensión de diferente polaridad. La polaridad de la fuente equivalente de tensión es la misma que la de la suma de mayor valor, como se muestra en la Fig. 3.9.
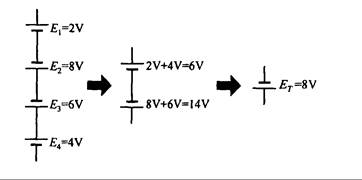
Fig. 3.10
La secuencia de dispositivos conectados en serie se puede cambiar y mantener el circuito funcionando sin verse afectado.
Los dos circuitos de la Fig. 3.11 tienen dos fuentes de tensión iguales y las mismas tres resistencias, de tal forma que son el mismo circuito.
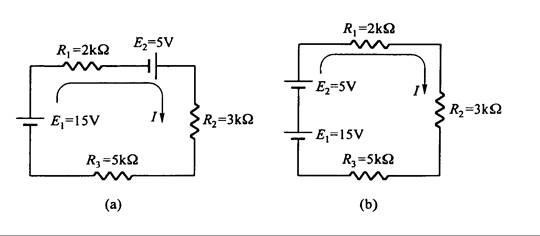
Fig. 3.11
Generalmente se necesita volver a dibujar el circuito para que sea fácil de leer. Por lo tanto es necesario idear la forma de indicar las posiciones con el objeto de simplificar los circuitos antes de analizarlos.
Ejemplo 3.4: Simplifique el circuito de la Fig. 3.13 como si fuera una única fuente de tensión y 4 resistencias en serie. Determine la dirección de la corriente y la magnitud del circuito equivalente

Fig. 3.12
Respuesta:
El circuito se puede volver a dibujar en dos pasos, como lo muestra la Fig. 3.13, pero debemos cambiar en forma correcta las fuentes de tensión, ya que es fácil de equivocarse y asignarles la polaridad equivocada. Probablemente el método más fácil es seguir el circuito para ir colocando cada una de las fuentes de tensión en su nueva posición.
Fig. 3.13
Finalmente, la corriente tiene dirección contraria al reloj, con una magnitud:
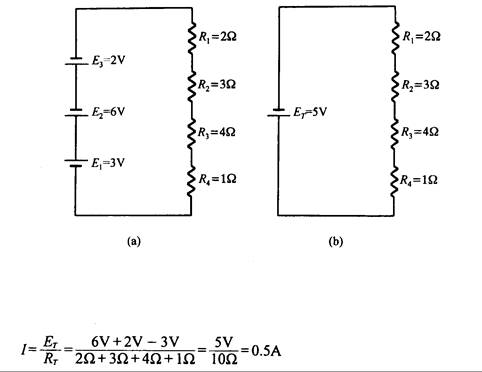
Como los dos circuitos (Fig. 3.12 y 3.13) son equivalentes, entonces son iguales las direcciones de las corrientes.
En la Fig. 3.14, la resistencia total es igual a 10 kW y la corriente I = 2 mA. De la Ley de Ohm sabemos que hay una caída de tensión V1 = 4.0 V en R1, y que para R2 es 4 veces mayor, por lo tanto, V2 = 16.0 V.
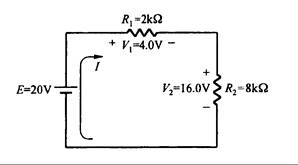
Fig. 3.14
De la Ley de Kirchhoff sabemos que la caída total de tensión debe ser igual al aumento de potencial en la fuente de tensión, es decir,
E = 20 V = 4V + 16V
Del anterior enunciado podemos obtener la regla de división de tensiones, que dice que la tensión aplicada en un circuito en serie producirá una caída proporcional de tensión en cada resistencia, según sea la magnitud de la resistencia. Esta regla se puede usar para determinar la caída de tensión en cada resistencia en serie sin tener que calcular primero la corriente. Cuando estudiamos la Ley de Ohm para determinar la corriente de un circuito resistivo en serie teníamos que la corriente es:
I = E / R (Amperios, A) (3.10)
De aquí que la resistencia total de las dos resistencias en la Fig. 3.14 es:
RT = R1 + R2
Usando de nuevo la Ley de Ohm, la caída de tensión de cualquier resistencia en el circuito es:
Vx = IRx
Sustituyendo ahora la ecuación (3.10) en la ecuación anterior, podemos expresar la ley de división de tensiones para dos resistencias como una simple ecuación:
Vx = (E / RT) Rx
En general, para cualquier cantidad de resistencias en serie, la caída de voltaje en cualquier resistencia es:
Vx = (Rx / RT) E
Ejemplo 3.5: Use la ley de división de la tensión en la Fig. 3.15 para calcular la caída de voltaje en cada resistencia. Verifique que la suma de las caídas de tensión es igual al aumento de tensión suministrado por la fuente de potencia del circuito.
Respuesta:
Ejemplo 3.6: Use la regla de división de tensiones para calcular la tensión en cada resistencia del circuito en la Fig. 3.6
La suma de caídas de tensión es:
Fig. 3.15
Respuesta:

Del ejemplo anterior obtenemos dos puntos importantes: Si una resistencia es mucho más alta que la otra en el circuito en serie, entonces la caída de potencial en esta resistencia más alta es casi igual a la tensión total. Por otro lado, si una resistencia es mucho más baja que la otra en el circuito en serie, entonces la caída de potencial en esta resistencia más baja es casi igual a cero. En general, si una resistencia en serie es unas 100 veces más que la otra resistencia en el circuito, entonces la resistencia más pequeña se puede ignorar.
La función de la tierra es proporcionar un punto de referencia o punto común para el circuito, y como potencial de referencia durante el diseño del circuito. El símbolo normalizado para la tierra se observa en la Fig. 3.17(a). El uso de este símbolo simplifica mucho el circuito. Se escoge cualquier punto en el circuito como punto de referencia (tierra), ya que esto no afecta las características del mismo. Los circuitos de la Fig. 3.18 son todos equivalentes, a pesar de que tienen diferentes puntos de referencia.
El bastidor metálico de los instrumentos generalmente están “aterrizados” mediante un alambre de tierra. Este tipo de método de aterrizar se denomina tierra del instrumento, cuyo símbolo se muestra en la Fig. 3.17(b).
Para evitar un golpe eléctrico, el cable de tierra generalmente se conecta utilizando la unión provista en la caja del instrumento. Si sucede algo anormal en el circuito, el bastidor puede canalizar el flujo de corriente en la dirección de la tierra (a manera de bypass del seccionador termomagnético o del fusible), evitando así que el operador no sufra daños.
Fig. 3.17
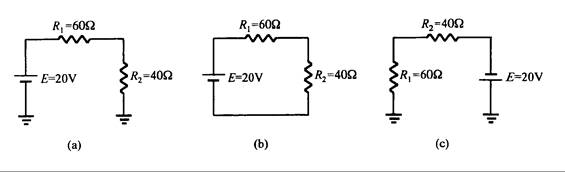
Fig. 3.18
Si deseamos expresar el potencial entre dos puntos (punto a y punto b en el circuito), entonces utilizamos subíndices (por ejemplo Vab). La primera letra indica un punto principal, y la segunda es un punto de referencia, lo que es una forma apropiada de indicación.
Considérese el circuito en serie de la Fig. 3.19:
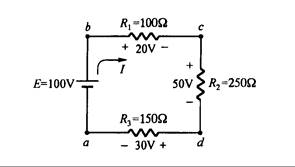
Fig. 3.19
Si llamamos a los nodos del circuito como a, b, c, y d, entonces sabremos que el nodo c tiene un potencial más alto que el nodo d, lo cual puede expresarse como Vcd = +50V, siendo redundante el signo positivo, y expresa que el potencial en c en más alto que en d. Si examinamos el potencial que debe haber entre el nodo d y el nodo c, encontramos que el potencial en el nodo d es más bajo que en c, lo que matemáticamente se expresa como Vdc = -50V. De lo anterior se obtiene la siguiente fórmula general:
Vcd = Vdc
Esto es válido para los nodos arbitrarios c y d del circuito.
La corriente que pasa por las resistencias inducen caídas de potencial en el circuito, como se muestra en la Fig. 3.19. Si llamamos en forma correcta a las caídas de potencial y a las polaridades de las resistencias, entonces se puede usar la siguiente fórmula:
Vbc = +20V Vcb = -20V
Vcd = +50V Vdc = -50V
Vda = +30V Vad = -30V
Si deseamos determinar el potencial entre dos nudos cualquiera del circuito, el método fácil es sumar todos los potenciales entre esos dos nodos. Debemos considerar la polaridad del potencial. El potencial o tensión entre los nodos b y d se puede determinar de la siguiente forma:
Vbd = Vbc + Vcd = 20V + 50V = +70V
De igual forma, el potencial entre b y a se encuentra mediante las caídas de tensión de las resistencias:
Vba = Vbc + Vcd + Vda = 20V + 50V + 30V = +100V
NOTA: el resultado anterior es correcto usando la fuente de tensión para determinar Vba. Este resultado explica que el potencial entre dos nodos es independientemente del camino que se tome.
Ejemplo: En la Fig. 3.20 encuentre el voltaje Vac, Vad, Vcf y Vab.

Fig. 3.20
Respuesta: Primero, es necesario determinar el voltaje equivalente:
Eeq = 8V + 6V – 4V = 10.0V
Esto hace que la corriente discurra en sentido contrario al reloj dentro del circuito. Use luego la regla de división de voltaje para determinar el potencial y la corriente de cada resistencia.
O se escoge la ruta opuesta y se obtiene:
Fig. 3.21
Finalmente, se calcula el potencial entre cada dos nodos:
El potencial entre cada resistencia se muestra en la Fig. 3.21

En un circuito con nodo de referencia, la mayoría de las tensiones (voltajes) se refieren a este punto. Bajo esta condición las tensiones ya no se expresan como subíndices dobles y si deseamos expresar el potencial de un nodo con respecto a tierra, lo podemos expresar como Va. De igual forma, el potencial del nodo b se puede expresar como Vb. De manera que el potencial de cualquier nodo requiere solamente un subíndice, y se sabe que está referido a la tierra del circuito.
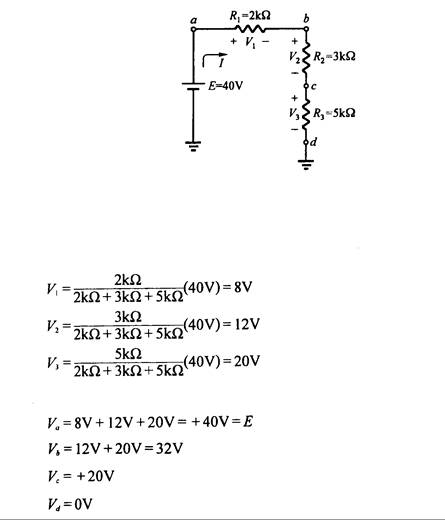
Ejemplo 3.8: Determine el potencial Va, Vb y Vd en la Fig. 3.22.
Ahora, el potencial en cada resistencia es el siguiente:
Fig. 3.22
Respuesta: use la regla de división de tensiones para determinar el potencial en cada resistencia.
Si hay algún potencial conocido que no está referido con respecto a la tierra, se puede calcular la tensión entre estos dos nodos a partir de la siguiente ecuación:
Vab = Va – Vb (Voltios, V)
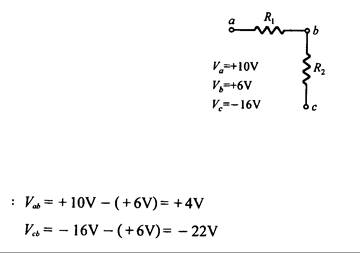
Ejemplo : En la Fig. 3.23, Va = +10V, Vb = +6V y Vc = -16V. Determine Vab y Vcb.
Fig. 3.23
Respuesta:
El concepto de tensión referida a tierra se puede extender a la fuente de tensión. Cuando una fuente de tensión se refiere a la tierra, se puede simplificar como una fuente puntual, como se muestra en la Fig. 3.24.
La fuente puntual se puede usar para simplificar el circuito. Debemos recordar en todo caso, que este punto en particular está siempre referido a la tierra, y en algunos casos ni siquiera se dibuja.
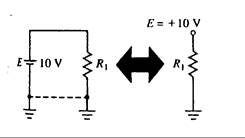
Fig. 3.24
Ejemplo 3.10. Determine la magnitud y dirección de la corriente en la Fig. 3.25
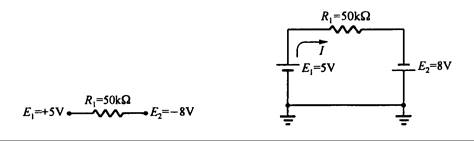
Fig. 3.25 Fig. 3.26
Respuesta: Este circuito se puede dibujar y enumerar, convirtiendo la tensión en expresiones comunes como se muestra en la Fig. 3.26. La corriente se puede calcular como:
I = ET / R1 = (5V + 8V) / (50 kW) = 0.26 mA
Hasta el momento hemos considerado solamente una fuente ideal de tensión, la cual posee una tensión constante y no tiene carga entre los dos terminales. Consideremos ahora una batería típica de automóvil, cuyo potencial es de unos 12V. De igual manera, tendremos 12V en ocho baterías en serie tipo C. ¿Cuál es la razón de no usar entonces 8 baterías tipo C en nuestro carro? La razón es que la batería de plomo – ácido tiene menos resistencia que las pilas de foco de baja energía. De hecho, todas las fuentes de tensión tienen resistencia interna, que es la le reduce a la fuente su desempeño. Podemos considerar como fuente ideal de tensión aquella que tiene la resistencia interna conectada en serie. La Fig. 3.27 una fuente de tensión ideal y otra real.
El potencial entre el terminal positivo y negativo es lo que se llama potencial entre terminales. En una fuente ideal de tensión, el potencial entre terminales se mantiene constante y no la afecta la carga. La tensión ideal proporcionará la corriente necesaria para llevar la carga. En la fuente real de tensión, sin embargo, el potencial entre terminales depende de la carga y la corriente suministrada estará limitada por la resistencia interna y por la carga.
Para la condición sin carga (RL = ¥ W) no hay corriente en el circuito, por lo que el potencial entre terminales es igual al potencial de la fuente. Si se tiene una salida en cortocircuito (RL = 0W), la corriente llegará a su máximo y el potencial entre terminales será cercano a cero. Bajo estas condiciones, la caída de potencial para la resistencia interna es igual al potencial de la fuente de tensión.
V
V
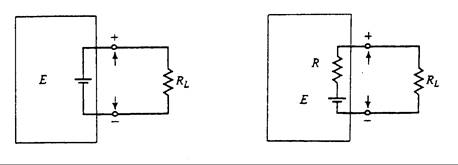
(a) Fuente ideal de tensión (b) Fuente real de tensión
Fig. 3.27
Ejemplo 3.11 El potencial en circuito abierto entre los terminales de potencial de cada una de las dos baterías es de 24 V. Se usan para alimentar una carga de 0.10W. Si una batería tiene 0.02W de resistencia interna y la otra 100W, calcule las corrientes a través de la carga y el potencial entre terminales de cada una de las baterías.
Respuesta: Los circuitos se muestran en la Fig. 3.28
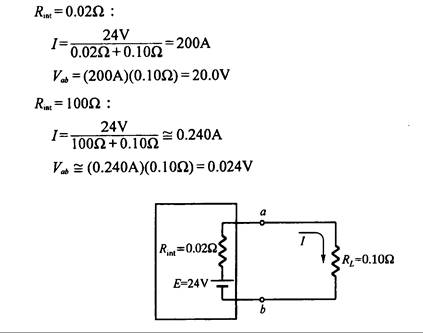
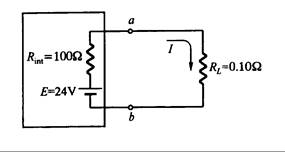
(b) Alta resistencia interna
1. Serie: Ambos terminales de dos dispositivos se conectan a una unión común y no existe ningún dispositivo con corriente conectado a esta unión.
2. Circuito en serie: El circuito es una combinación de dispositivos en serie.
3. La corriente a través de cada dispositivo de un circuito en serie es la misma.
3.11 Problemas
1. Determine las tensiones desconocidas en la Fig. 3.29
2. Determine las tensiones desconocidas en la Fig. 3.30
Fig. 3.29
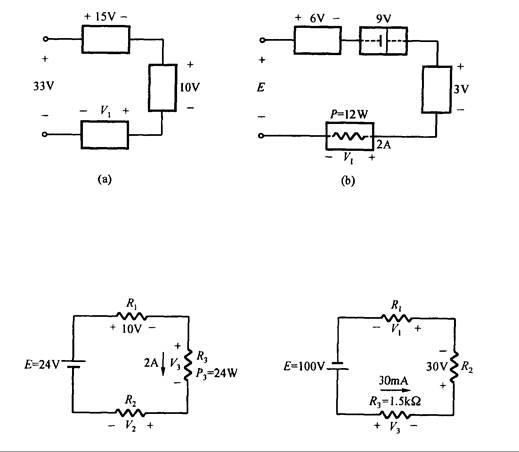
Fig. 3.3. Fig. 3.31
3. Determine las tensiones desconocidas en la Fig. 3.31
4. Determine las tensiones desconocidas en la Fig. 3.32
donde:
5. Determine la resistencia total RT y la corriente I en la Fig. 3.33
Fig. 3.32
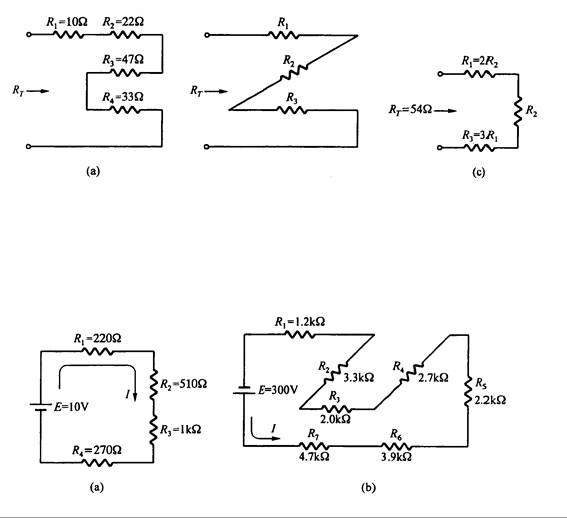
6. La resistencia total en la Fig. 3.34 para cada circuito es RT. Para cada uno de ellos proporcione las respuestas.
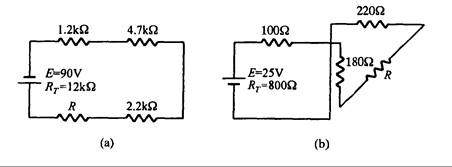
Fig. 3.34
7. Calcule los siguientes valores para el circuito de la Fig. 3.35
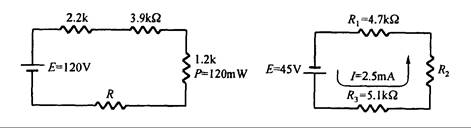
Fig. 3.35 Fig. 3.36
8. En la Fig. 3.36 la corriente es de 2.5 mA. Calcule los siguientes valores:
9. En la Fig. 3.37 calcule:
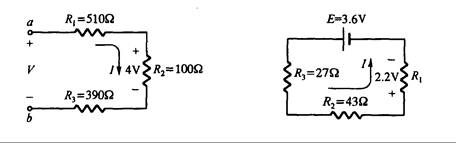
Fig. 3.37 Fig. 3.38
10. En el circuito de la Fig. 3.38,
11. En el circuito de la Fig. 3.39,
1/8W, 1/4W, 1/2W, 1W, y 2W.
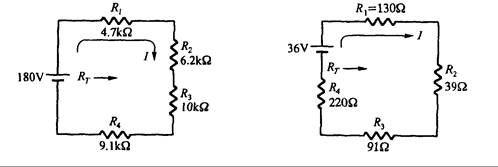
Fig. 3.39 Fig. 3.40
12. Repita el problema 11 utilizando el circuito de la Fig. 3.40
13. Para la Fig. 3.41:
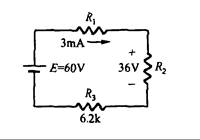
Fig. 3.41
Fig. 3.43
16. Use la regla de división del voltaje para calcular el potencial de cada resist. en la Fig. 3.44. Verifique la Ley de Kirchhoff con los resultados
Fig. 3.42
15. Utilice los valores conocidos el los circuitos de la Fig. 3.43 para determinar la polaridad y el valor de las fuentes de potencial
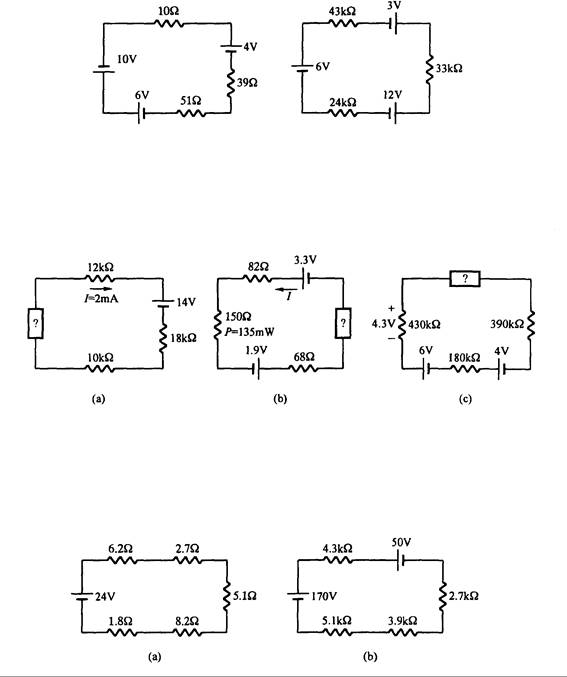
Fig. 3.44
17. En la Fig. 3.45:
Fig. 3.45
18. Determine el potencial Vab y Vbc en el circuito de la Fig. 3.46
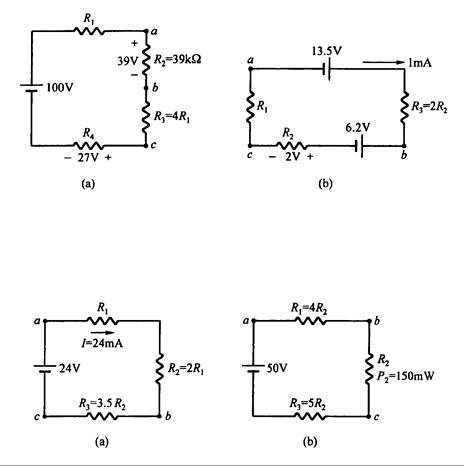
Fig. 3.46
19. En el circuito de la Fig. 3.47, determine el potencial en cada resistencia y calcule el potencial Va.
Fig. 3.47
20. En el circuito de la Fig. 3.48:
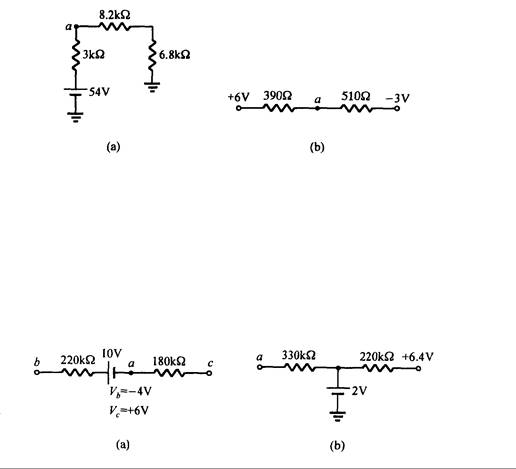
Fig. 3.48
21. Una batería tiene un potencial abierto entre terminales de 14.4V. Cuando la batería se conecta a una carga de 100W, el potencial entre los bornes cae a 6.4V.
Fuente del documento: https://profejuandotcom.files.wordpress.com/2014/03/capc3adtulo-3-circuitos-serie.doc
Sitio para visitar: https://profejuandotcom.files.wordpress.com
Autor del texto: no especificado en el documento de origen o se indique en el texto
Las letras son propiedad de sus respectivos autores y les damos las gracias por la oportunidad que nos brindan para conocer sus textos libres para fines ilustrativos y educativos. Si usted es el autor del texto y que está interesado para solicitar la eliminación del texto o la inserción de otra información envíe un correo electrónico después de que los controles adecuados que va a satisfacer su solicitud tan pronto como sea posible.
Los resúmenes, toma nota de los textos que figuran en nuestra página web se ponen a disposición de forma gratuita con fines didácticos de la ilustración, científica, social, civil y cultural a todos los posibles interesados de acuerdo con el concepto de uso justo, y con el 'objetivo de cumplimiento de la Directiva Europea 2001/29 / CE y del «arte. 70 de la ley 633/1941 sobre derechos de autor
La información médica y de la salud en este sitio es de carácter general y para propósitos informativos solamente y por lo tanto no puede en ningún caso sustituir el consejo de un médico (o un autorizado legalmente a la profesión).