Ley de Ohm

 

• Introducción

En el presente capítulo presentaremos la Ley de Ohm, que constituye una de las partes más importantes y fundamentales de la electricidad. Se aprenderá a usar la Ley de Ohm para calcular tensión, corriente, resistencia y la manera de juzgar la polaridad de la tensión y corriente en un circuito.

• Ley de Ohm

 

En términos simples la Ley de Ohm consiste en aplicar una resistencia a una diferencia de potencial o tensión, con el resultado de que habrá una corriente pasando por el circuito.

Georg Simon Ohm descubrió que si la resistencia se mantiene constante en el circuito, la corriente aumentará proporcionalmente cuando se aumenta la tensión o voltaje. De igual manera, si la resistencia se mantiene constante pero disminuye al aplicar la tensión, entonces la corriente disminuirá en forma proporcional. Asimismo, descubrió que si la tensión se mantiene constante pero se aumenta la resistencia, entonces la corriente se disminuye, y también, manteniendo el voltaje constante pero disminuyendo la resistencia, se aumenta la corriente. Estos fenómenos le permitieron a Ohm concluir que la corriente es proporcional a la tensión e inversamente proporcional a la resistencia del circuito de CD.

La Fig, 2.1 muestra un circuito con una batería y una resistencia. Se emplea un medidor eléctrico para medir la tensión entre los dos terminales de la resistencia, y la corriente a través de la misma. El resultado confirma la Ley de Ohm, que se puede expresar como:

 

                                    I = E / R (Amperios, A)                                          (2.1)

 

donde:           E es la tensión, usando el Voltio (V) como unidad
R es la resistencia, con el Ohmio (W) como unidad, e
I es la intensidad o corriente, con el Amperio (A) como unidad.

 

En la ecuación (2.1) se comprende que entre mayor sea la tensión, obtendremos una mayor corriente. Esta relación se puede verificar con la Fig. 2.2, comparando los tres circuitos (a), (b) y (c), donde la resistencia tiene un mismo valor de 10 W. En (a), la tensión suministrada es de 10 V, I = E/R = 10 V/10W = 1 A. En (b), la tensión es de 20V, I = E/R = 20 V/10W = 2 A. En (c), la tensión es de 30V, I = E/R = 30 V/10W = 3 A.

De tal manera que, para una resistencia constante, al duplicar la tensión se duplica la corriente. Triplicando la tensión se triplica la corriente.

 

 

               

 

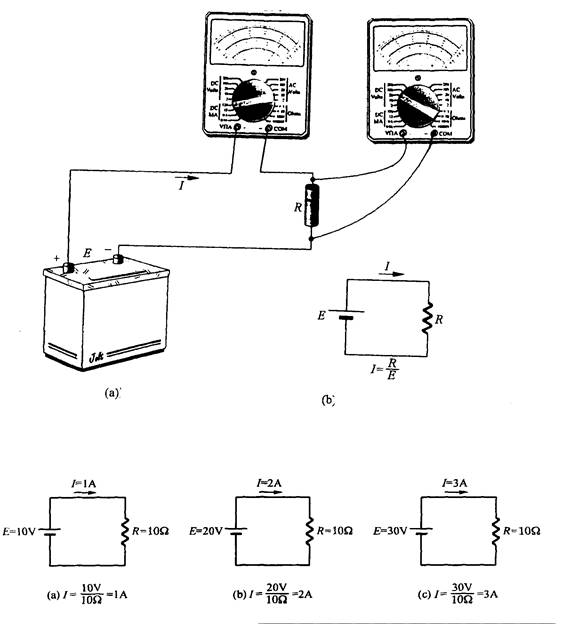
            Fig. 2.2 – La Tensión es directamente proporcional a la corriente

           

En la fórmula de Ohm, la resistencia es inversamente proporcional a la corriente. En la Fig. 2.3, al duplicar la resistencia bajo una tensión constante, como se muestra en (b), la corriente se reduce a  la mitad. En la Fig. (c), la corriente es un tercio del valor original, etc.

 

 

La Ley de Ohm puede también expresarse como:

              

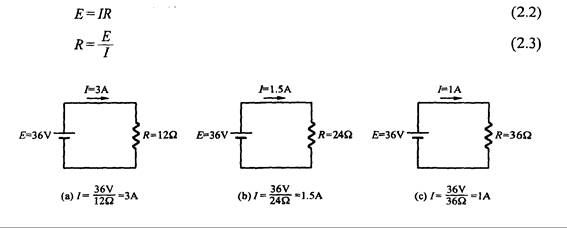
Fig. 2.3 – La resistencia es inversamente proporcional a la corriente

 

            Las ecuaciones (2.1), (2.2) y (2.3) se pueden derivar utilizando simples operaciones algebraicas. Se usan en forma individual según se necesiten.

 

            La ecuación (2.1) proporciona el voltaje o tensión y se deriva de la que se conoce para la corriente y la resistencia. El voltaje es igual al producto de amperios por ohmios. Por ejemplo, si se tiene una resistencia de 50 W y una corriente de 2 A, entonces se puede conocer la tensión del circuito, 100 V.

                        E = I x R
E = 2 x 50
E = 100

 

La ecuación (2.2) sirve para calcular la corriente y se deriva de las que se conocen para tensión y resistencia. En el ejemplo que tenemos, si se  tiene una tensión de 120 V conectada a una resistencia de 30 W, entonces se sabe que la corriente es de 4 A:

                        I = E / R
I = 120 / 3
I = 4

 

La ecuación (2.3) describe a la resistencia y se puede derivar de las ecuaciones conocidas para tensión y corriente. Asumiendo que se tiene un circuito con una tensión de 240 V y una corriente de 10 A, entonces la resistencia es de 24 W.

 

                        R = E / I
R = 240 / 10
R = 24
La Fig. 2.4 es un diagrama simple para que el estudiante recuerde la Ley de Ohm. Es necesario cubrir con el dedo la magnitud deseada. Por ejemplo, si se necesita la tensión, debemos cubrir la E en el diagrama, quedando I x R, ya que E = I x R. Este método se usa también para obtener la corriente (I) y la resistencia (R).

                  

Fig. 2.4 – Diagrama basado en la Ley de Ohm

Ejemplo 2.1: Si se conecta una resistencia de 27 W a una batería de 12 V, ¿cuál es la corriente?

Respuesta: Usando la Ley de Ohm tenemos:

                        I = E / R = 12 V / 27 W = 0.444 A

 

Ejemplo 2.2: En la Fig. 2.5 el bombillo eléctrico está conectado a una batería de 6V y la corriente es de 25 mA. ¿Cuál es la resistencia del bombillo?

 

                                      

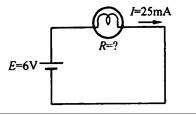
Respuesta: Utilizando la ecuación (2.3) para obtener R:

            R = E / I = 6V / 25 x 10-3 A = 240 W

 

 

Ejemplo 2.3 : Se tiene una resistencia con código de colores café, rojo y amarillo conectada a una fuente de 30 Voltios. ¿Cuál es I ?

Respuesta: El valor desconocido aquí es I, por lo que debemos usar la ecuación (2.1). La resistencia, según el código de colores es  R = 120 kW.

                        I = E / R = 30V / 120 kW = 0.25 x 10-3 mA

 

2.3  La polaridad de la tensión y de la corriente

• Polaridad de la Tensión

 

Es muy importante conocer la polaridad de la tensión y de la corriente en un circuito electrónico. Por lo menos se debe poder conectar correctamente las puntas (+) y (-) de un multímetro. Si la posición de las puntas es errónea, la aguja girará hacia la izquierda y no se podrá leer el resultado, arruinándose el instrumento. Si el multímetro es de tipo digital, una conexión incorrecta influirá en el signo negativo o positivo.

Para comprender mejor la diferencia que existe entre las polaridades de la tensión, véase la Fig. 2.6. La fuente de tensión está conectada directamente a la resistencia. Obviamente la polaridad positiva está en la posición superior y la negativa en la posición inferior. La corriente fluye desde arriba hacia abajo, de tal forma que para ver la polaridad de la tensión podemos considerar que la cola de la flecha es positiva y que la punta de la misma es negativa, como en (b).

   

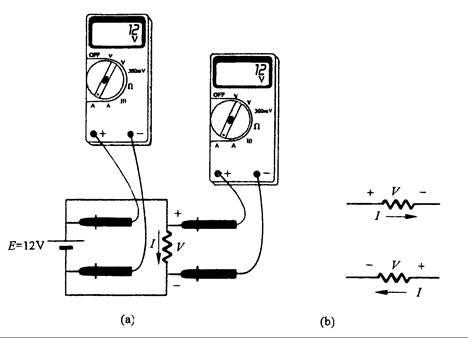
Fig. 2.6 – Polaridad de la tensión
El signo negativo en un multímetro digital significa que la polaridad medida es opuesta a la polaridad real, como se muestra en la Fig. 2.7.

 

 

Veamos ahora con cuidado la dirección de la corriente. Generalmente usamos el terminal con signo (+) de la fuente de tensión como el punto de donde sale la corriente, como se muestra en la Fig. 2.8(a). Aquí, I = E / R = 10V / 2W = 5 A, con la dirección que se muestra. Sin embargo, ¿cómo se puede determinar la dirección si de antemano no se conoce?. Esta situación la encontrará a menudo cuando se analizan circuitos más complejos.

Para obtener la respuesta a esta pregunta, analice la Fig. 2.8(b), donde se muestra que la corriente fluye hacia el terminal positivo de la fuente de tensión. Para corregir la dirección, cambiaremos los signos positivo y negativo de la corriente. Por lo tanto, (a) y (b) son lo mismo. Esto significa que hay dos formas de expresar la corriente para una corriente, lo que nos da las siguientes reglas: el valor es positivo si la flecha de referencia tiene la dirección real de la corriente. Si es opuesta a la dirección de referencia, el valor es negativo. De hecho, esto implica que arbitrariamente se le puede asignar la dirección a la corriente. Por lo tanto, cuando se obtiene un valor negativo significa que la dirección asignada es opuesta a la verdadera dirección de la corriente.

 

 

 

              

• La polaridad medida es la misma que la polaridad verdadera. El funcionamiento es el mismo que el de la polaridad de la tensión
• La polaridad medida es diferente que la polaridad verdadera. El funcionamiento es diferente al de la polaridad de la tensión

 

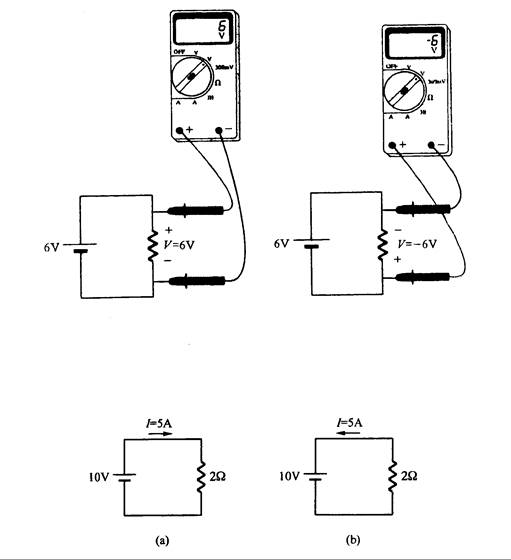
Fig. 2.8 – El símbolo de la corriente

 

 

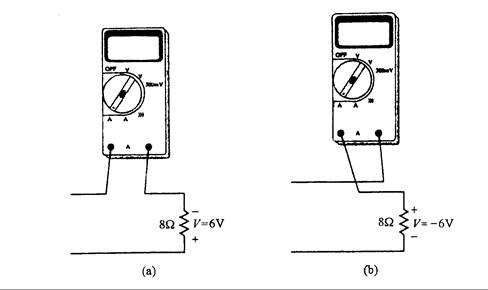
Ejemplo 2.4: En relación con la Fig. 2.9 con (a),  I = 3A y (b), I = -3A. Determine la tensión entre la resistencia según la notación de polaridad de la tensión, y verifique que ambas son iguales.

                                    
Fig. 2.9 – Determinación de la dirección de la corriente

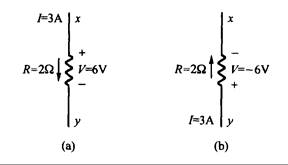
Respuesta: Póngale el signo positivo en la cola de las flechas de la corriente. Primero, en (a), la polaridad de x con respecto a y es V = IR = (3 A)(2W) = 6V. En (b), el signo de la polaridad expresa a y con respecto a x, y el voltaje es:
V = IR = (-3 A)(2W) = -6V. Es decir, de y hacia x es –6V, o de x hacia y es 6V, de tal forma que ambos son el mismo voltaje.

• Potencia

 

La potencia no es desconocida para nosotros. Por ejemplo, en el calentador de agua o en un bombillo de luz se usa el Watt como unidad de medida. Una cantidad alta de watts significa que el dispositivo puede disipar más energía por segundo. Esto significa que un bombillo de 100 W produce más luz que otro de 40 W, y la potencia disipada por el primero será mayor, también.

De tal forma que la potencia es dependiente de la disipación de la misma, es decir, de la capacidad de hacer trabajo. La potencia se puede definir como la relación mediante la cual se convierte el trabajo en energía. El símbolo de la potencia en P y la definición se escribe como:

            P = W / t  (Watt, W)                                                            (2.4)

Aquí, W es la potencia, medida en Julios, y t es el tiempo en segundos.

 

            Nos interesa la potencia eléctrica, de tal manera que necesitamos usar la carga eléctrica para expresarla como P. La diferencia de potencial o simplemente potencial se define como el trabajo realizado sobre la carga, y la corriente se define como la tasa de transferencia de la carga, es decir:

 

                        V = W / Q                                                                             (2.5)

e                     I = Q / t                                                                                  (2.6)

 

 

De la ecuación (2.5), donde W = QV, lo sustituimos en la ecuación (2.4) para obtener que P = W / t = (QV) / t = V(Q / t), y reemplazando Q / t por I :

                        P = V x I  (Watt, W)                                                            (2.7)

También:
P = E x I  (Watt, W)                                                            (2.8)

Y una mejor relación se obtiene si se sustituye V = IR e I = V / R en la ecuación (2.8):

P = I2 x R  (Watt, W)                                                           (2.9)

Y                     P = V2 / R                                                                             (2.10)

                       
Ejemplo 2.5 : Utilice las fórmulas para calcular la potencia del calentador de la Fig. 2.10

 

                        

 

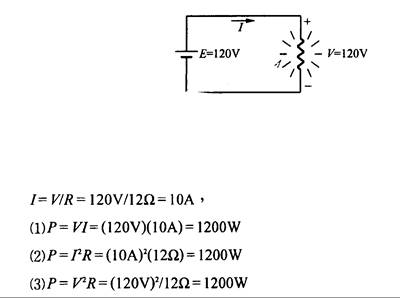
Nota: los resultados son los mismos usando las diferentes fórmulas.

 

 

 

 

 

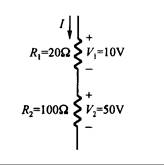
Ejemplo 2.6: Use la ecuación (2.10) para calcular la potencia de cada uno de los transistores de la Fig. 2.11.

                                                             
Respuesta:

 

• Dirección de la Potencia

 

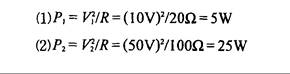
En un circuito con una fuente de potencia y una carga, la energía va desde la fuente de potencia hasta la carga. La dirección es obvia. En un circuito con múltiples fuentes de potencia y cargas, no es tan fácil comprender qué camino toma la potencia, de tal manera que debemos definir claramente la dirección en que se transmite la potencia.

La carga producida por la resistencia en la Fig. 2.12 se puede usar para explicar este concepto. La energía solamente puede fluir hacia la resistencia y no puede fluir fuera de ella (la resistencia no puede crear energía). Definimos el camino por donde se transporta la energía como positivo aquel que va desde la fuente hacia la carga, como se muestra en (a). Utilizamos una flecha ® para expresar este concepto, lo que significa que es positiva cuando el camino por donde se transporta la potencia es el mismo que la dirección que tiene la flecha en la Fig. 2.12(a). Si tiene una dirección opuesta a la de la flecha, entonces es negativa.

Para poder explicar las reglas, consideremos los terminales de la fuente de potencia de la Fig. 2.12(b). Cuando la flecha de la corriente y de la potencia apuntan hacia fuera, la salida de potencia es positiva. Tanto I como P son positivos. La polaridad de la tensión se da por definición.

            Considerando la carga en la Fig. 2.12(c), nótese que la correspondiente polaridad de la tensión, la dirección de la corriente y la flecha de la potencia de la carga. Podemos decir que cuando la corriente y la potencia apuntan hacia la carga, la potencia de la carga es positiva. La polaridad de la tensión o voltaje se da por definición.

 

En la Fig. 2.12(d) se puede observar este concepto. En la caja puede haber una fuente de tensión o una carga; si P es positivo, se transportará la potencia hacia la caja. De lo contrario, la potencia saldrá de la caja.

                

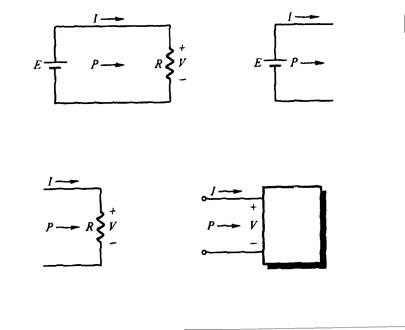
Fig. 2.12 – Definición de la dirección de la potencia

 

• Resumen

Puntos clave:

• Ley de Ohm:       I = V / R,

V = I x R,
R = V / I

• El voltaje es directamente proporcional a la corriente, y la corriente es inversamente proporcional a la resistencia.

 

• El terminal por donde la corriente fluye hacia la resistencia es positivo, y el terminal por donde sale la corriente de la resistencia es negativo.

• Potencia = W / t = Vx I = I2 x R = V2 / R

 

• Símbolo de la Potencia: positivo para suplir potencia y negativo para disipar potencia.

 

 

• Problemas

• Determine la corriente I en los siguientes problemas y exprese las respuestas en las unidades adecuadas: A, mA, mA, etc.
• E = 40V, R = 20W
• E = 35 mV, R = 50W
• E = 100V, R = 50kW
• E = 60V, R = 2.5 mW
• E = 7.5V, R = 2.5 x 103W
• E = 12 kV, R = 2 MW

 

• Determine la resistencia R en los siguientes problemas, y exprese las respuestas en las unidades adecuadas: W, kW, MW, etc.
• E = 40V, I = 2.5 A
• E = 37.5V, I = 1 mA
• E = 2 kV, I = 0.1 kA
• E = 4 kV, I = 8 x 10-4 A

• Determine la tensión en los siguientes problemas:
• 1 mA, 40 kW
• 10 mA, 30 kW
• 10 mA, 4 x 104 W
• 12 A, 3 x 10-2W

 

• Si en un circuito la corriente es de 50 mA, ¿cuál es la tensión en la resistencia de 560 W en el circuito?

• Una fuente de potencia de 120V produce 12.5 A de corriente en el calentador, ¿cuál es la resistencia?

 

• Se aplican 20V de tensión en una resistencia con código de colores café, negro, rojo y plateado.

 

• Calcule la corriente normal en el circuito.
• Calcule la corriente mínima y máxima de acuerdo con la posible resistencia (inducida por la tolerancia de la resistencia)

• En la Fig. 2.13, si F = 156V, ¿cuál será la indicación del voltímetro?

 

 

 

 

 

                              

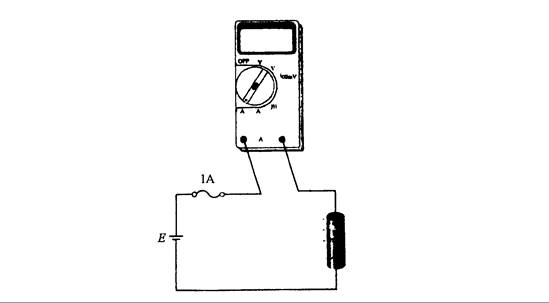
Fig. 2.13

• En la Fig. 2.14 el amperímetro indica automáticamente la polaridad. Determine el valor de la misma. Nota: cuando la corriente fluye al terminal A, el amperímetro muestra un valor positivo.

 

  
Fig. 2.14

 

• Una batería de 12V puede entregar una corriente de 3 A a una resistencia. ¿Cuánta energía le entregará a la resistencia?

 

• En un circuito de 120 V están conectados seis bombillos de 100 W, un calentador de 1.2 kW y un motor eléctrico de 1500 W. El fusible está calculado para 30 A. ¿Qué sucede cuando al circuito se le agrega un tostador de 900 W?